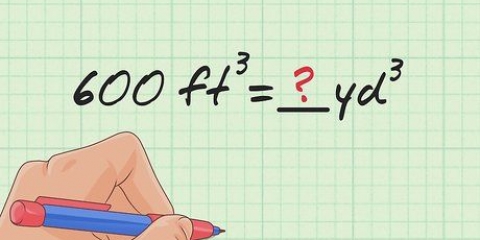Konvertering af et decimaltal til et oktal (med billeder)

Indhold

Trin
- Metode 1 af 2: Konvertering ved deling
- Metode 2 af 2: Konvertering ved at bruge resten
Øvelser

Oktal er basis 8 talsystemet, hvor kun cifrene 0 til 7 bruges. Den største fordel er den lethed, hvormed du konverterer til binært (grundtal 2), fordi hvert ciffer i et oktal kan skrives som et unikt trecifret binært tal. At konvertere fra decimal til oktal er lidt vanskeligere, men du behøver ikke mere matematik end lang division for at gøre dette. Start med divisionsmetoden, hvor du bestemmer hvert tal ved at dividere det med 8 potenser. Resten metoden er hurtigere og bruger samme måde at regne på, men kan være lidt sværere at forstå.

Trin

Metode 1 af 2: Konvertering ved deling

1. Brug denne metode til at lære begreberne. Af de to metoder på denne side er denne metode den nemmeste at forstå. Hvis du allerede er vant til at arbejde med forskellige talsystemer, så prøv hvilemetoden nedenfor, som er lidt hurtigere.

Billede med titlen Konverter fra decimal til oktal Trin 2

2. Skriv decimaltallet ned. I dette eksempel vil vi konvertere tallet 98 til et oktal.

Billede med titlen Konverter fra decimal til oktal Trin 3

3. Angiv magterne i 8. Glem ikke at "decimal" har grundtallet 10, fordi hvert ciffer i et tal i dette system er en potens af 10. Vi kalder de første 3 cifre for enheder, tiere og hundreder - men vi kan også skrive 10 , 10 og 10. Oktale tal, eller dem med grundtallet 8, bruger potenser 8 i stedet for 10. Skriv nogle af disse potenser af 8 på en vandret linje, fra største til mindste. Bemærk, at alle disse tal er skrevet som decimaler (grundlag 10):

8 8 8

Omskriv dette som:

64 8 1

Du behøver ikke potenser af 8 større end dit oprindelige tal (i dette tilfælde 98). Da 8 = 512 og 512 er større end 98, kan vi lade det ude af tabellen.

Billede med titlen Konverter fra decimal til oktal Trin 4

4. Divider decimaltallet med tallet med den største potens af 8. Se nøje på decimaltallet: 98. De ni på tierpladsen indikerer, at der er 9 tiere i dette tal. 10 går 9 gange i dette tal. Ligeledes vil vi med oktaltallet gerne vide, hvor mange gange "64" går ind i det endelige nummer. Divider 98 med 64 for at bestemme dette. Den nemmeste måde at gøre dette på er at bruge en tabel, læst fra top til bund:

98
÷

64 8 1
=

1 ← Dette er det første ciffer i dit oktale tal.

Billede med titlen Konverter fra decimal til oktal Trin 5

5. Bestem resten. Beregn resten af divisionsproblemet, eller det tal, der er tilbage og ikke længere passer helt. Skriv dit svar øverst i anden kolonne. Dette er, hvad der er tilbage af dit nummer, efter at det er blevet beregnet første cifre. I vores eksempel er 98 ÷ 64 = 1. Da 1 x 64 = 64, er resten 98 - 64 = 34. Tilføj dette til din tabel:

98 34
÷

64 8 1
=

Billede med titlen Konverter fra decimal til oktal trin 6

6. Divider resten med næste potens af 8. For at bestemme det næste ciffer går vi videre til næste potens af 8. Divider resten med dette tal og udfyld den anden kolonne i din tabel:

98 34
÷ ÷

64 8 1
= =

1 4

Billede med titlen Konverter fra decimal til oktal trin 7

7. Bliv ved med dette, indtil du finder det komplette svar. Bestem som før resten af dit svar og skriv det øverst i næste kolonne. Fortsæt med at dividere og bestemme resten, indtil du har gjort dette for hver kolonne, inklusive 8 (enhederne). Den sidste række er det sidste decimaltal, omregnet til et oktal. Her er vores eksempel med tabellen fuldstændigt udfyldt (bemærk, at 2 er resten af 34÷8):

98 34 2
÷ ÷ ÷

64 8 1
= = =

1 4 2

Det endelige svar: 98 med grundtal 10 = 142 med grundtal 8. Du kan skrive dette som 98₁₀ = 142₈

Billede med titlen Konverter fra decimal til oktal trin 8

8. Tjek dit arbejde. Det gør du ved at gange hvert ciffer i oktaltallet med 8-potensen, det repræsenterer. Du bør så få det originale nummer igen. Lad os tjekke svaret, 142:

2 x 8 = 2 x 1 = 2

4 x 8 = 4 x 8 = 32

1 x 8 = 1 x 64 = 64

2 + 32 + 64 = 98, det tal vi startede med.

Billede med titlen Konverter fra decimal til oktal trin 9

9. Prøv følgende øvelsesproblem.Øv metoden ved at konvertere 327 til et oktal tal. Når du tror, du har fundet svaret, skal du vælge den usynlige tekst nedenfor for at se effekten af hele problemet.

Vælg dette stykke:

327 7 7
÷ ÷ ÷

64 8 1
= = =

5 0 7

Svaret er 507.

(Tip: 0 kan sikkert være svaret på et underproblem.)

Metode 2 af 2: Konvertering ved at bruge resten

Billede med titlen Konverter fra decimal til oktal trin 10

1. Start med et decimaltal. Vi starter med nummeret 670.

Denne metode er hurtigere end sekventiel division. De fleste mennesker synes, at dette er meget sværere at forstå, og vil måske finde det mere behageligt at starte med den simplere metode ovenfor.

Billede med titlen Konverter fra decimal til oktal trin 11

2. Divider dette tal med 8. Ignorer for nu tallene efter decimaltegnet. Du vil snart se, hvorfor denne beregning er nyttig.

I vores eksempel: 670 8 = 83.

Billede med titlen Konverter fra decimal til oktal trin 12

3. Bestem resten. Nu vi så ofte vi kan "divideret med 8", en lille rest er tilbage. Dette er det sidst ciffer i vores oktale tal, i stedet for enhederne (8). Resten er altid mindre end 8, så det kan repræsenteres af et hvilket som helst af de andre cifre.

I vores eksempel: 670 ÷ 8 = 83 resten 6.

Vores oktale tal er indtil videre ???6.

Hvis din lommeregner har en "modul" eller "mod"-knappen, kan du bestemme denne værdi ved at indtaste: "670 mod 8."

Billede med titlen Konverter fra decimal til oktal trin 13

4. Del svaret på divisionsproblemet med 8. Hold resten til side og vend tilbage til delingsproblemet. Tag svaret og divider det igen med 8. Skriv svaret ned og afgør resten. Dette er det næstsidste ciffer i oktaltallet, 8 = 8s pladsen.

I vores eksempel: Svaret på det sidste underproblem er 83.

83 ÷ 8 = 10 resterende 3.

Vores oktale tal er indtil videre ??36.

Billede med titlen Konverter fra decimal til oktal trin 14

5. Divider med 8 igen. Som før divider du svaret på den sidste opgave med 8, og find resten. Dette er det tredje til sidste ciffer i oktaltallet, 8 = 64 pladsen.

I vores eksempel: Svaret på det sidste delproblem er 10.

10 ÷ 8 = 1 rest 2.

Vores oktale tal er indtil videre ?236.

Billede med titlen Konverter fra decimal til oktal trin 15

6. Gentag dette, indtil du har bestemt det sidste tal. Hvis du har regnet den sidste delopgave, så er svaret nul. Resten af dette problem er det første ciffer i oktaltallet. Du har nu fuldstændig konverteret decimaltallet.

I vores eksempel: Svaret på det sidste delproblem er 1.

1 ÷ 8 = 0 resten 1.

Vores endelige svar er det oktale tal 1236. Vi kan skrive dette som 1236₈ for at vise, at dette er et oktal tal.

Billede med titlen Konverter fra decimal til oktal trin 16

7. Forstå, hvordan dette fungerer. Hvis du har svært ved at forstå denne metode, er her en forklaring:

Du starter med en stak på 670 enheder.

Den første delopgave opdeler dette i grupper, 8 enheder pr. gruppe. Det, der er tilbage, resten, passer ikke ind i ottetallene i oktaltallet. Så det skal være på enhedernes plads.

Tag nu stakken af grupper og opdel den i sektioner med hver 8 grupper. Hver sektion har nu 8 grupper med hver 8 enheder eller 64 enheder i alt. Resten passer ikke ind her, så det hører ikke hjemme i stedet for de 64 numre. Det skal være i stedet for de 8 numre.

Dette fortsætter, indtil du har bestemt hele tallet.

Øvelser

Prøv selv at konvertere følgende decimaltal ved hjælp af en af metoderne ovenfor. Når du tror, du har fundet svaret, skal du markere den usynlige tekst til højre for lighedstegnet for at kontrollere. (Noter det ₁₀ decimal betyder og ₈ oktal.)
99₁₀ = 143₈
363₁₀ = 553₈
5210₁₀ = 12132₈
47569₁₀ = 134721₈