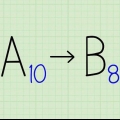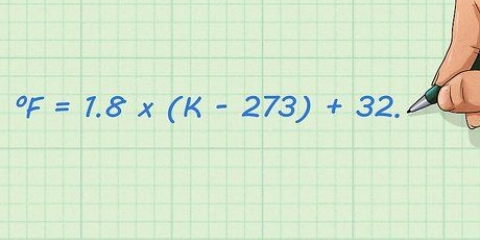Konverter binær til oktal

1. Genkend en række binære tal. Binære tal er simpelthen sekvenser af enere og nuller, såsom 101001, 001 eller endda kun 1. Når du ser sådan en talrække, er den normalt binær. Nogle bøger og lærere henviser dog også til binære tal med et `2`-abonnement, såsom 1001₂, dette for at undgå forveksling med decimaltallet 1001.

• Dette subscript angiver `basis` for nummeret. Binært er et talsystem med base to og oktal har base otte.

2. Gruppér alle eterne og nullerne i binæren i sæt af tre, startende fra højre. Der er kun to forskellige binære og otte oktale cifre. Fordi $2^{}$ har du brug for tre binære tal til at repræsentere hvert oktal tal. Begynd at opdele i grupper til højre. For eksempel: det binære tal 101001 kan derefter opdeles i 101 001.

3. Tilføj nuller til venstre for det sidste ciffer, hvis du ikke har nok cifre til at lave en gruppe på tre tal. Det binære tal 10011011 har otte cifre, ikke et multiplum af tre, men kan stadig konverteres til et oktal tal. Tilføj blot ekstra nuller til den første gruppe, indtil den har tre pladser. For eksempel:

4. Tilføj en 4, 2 og en 1 til hver streng med tre tal for at angive stedværdierne. Hvert af de tre binære tal i et sæt repræsenterer en bestemt pladsværdi i det oktale talsystem. Det første tal er det ene for en 4, det andet et 2, og det tredje har værdien 1. For klarhedens skyld skal du skrive dette direkte under hver streng af tre binære tal. For eksempel:

5. Hvis der er en over en af ​​stedværdierne, skal du skrive det tal (4, 2 eller 1) for at begynde konverteringen. Hvis der er en over "4" så indeholder oktaltallet en 4. Hvis der er et 0 over pladsværdien 1, så indeholder oktaltallet ikke 1, så sæt et mellemrum, nul eller bindestreg på det sted. Som i følgende eksempel:

6. Læg de nye tal sammen i hver gruppe med tre cifre. Hvis du ved, hvilke stedværdier der er i det oktale tal, skal du lægge alle cifrene sammen per gruppe. Så hvis du har 101, bliver dette 4, 0 og 1, og det giver 5 på som følge heraf ($4+0+1=5$). For at fortsætte med eksemplet ovenfor:

7. Placer de nyligt konverterede svar side om side for at danne det endelige oktale tal. Delingen af ​​det binære tal var blot for at gøre konverteringen nemmere - det oprindelige tal var en lang streng. Så nu hvor det er konverteret, sæt det hele sammen igen for at få dit endelige svar. Det er ikke mere.

8. Tilføj en subscript 8 (som denne ₈) for at fuldføre konverteringen. Der er dybest set ingen måde at vide, om 523 refererer til et oktalt eller et decimaltal uden den korrekte notation. For at sikre, at din lærer ved, at du har løst problemet korrekt, skal du sætte et sænket 8-tal ved siden af ​​dit svar, med henvisning til et oktalt tal (grundlag 8).

1. Brug en simpel konverteringstabel for at spare tid og arbejde. Du kan ikke bruge dette på en test, men på andre tidspunkter er det et godt valg. Da der kun er 8 mulige kombinationer af tal, er det faktisk en ret nem tabel at huske. Det eneste du skal gøre er at dele tallene op i grupper af tre og sammenligne dem med tabellen på billederne.

• Bemærk, hvordan der for tallene 8 og 9 ikke er nogen direkte konverteringer. I oktale tal eksisterer de ikke da der kun er 8 cifre (0-7) i et grundtal med 8 tal.

2. Forlad decimaltegnet og find ud af, om du har at gøre med decimaler. Antag, at du skal konvertere det binære tal 10010.11 til et oktalt tal. Normalt arbejder man fra højre mod venstre for at dele tallene op i grupper af tre. Med en decimal arbejder du udad fra punktet. Så for cifrene til venstre for decimaltegnet (10010), arbejd fra prikken til venstre (010 010 eller konverteret, 115,24). For tallene til højre (0,11) skal du arbejde fra punktet til højre (110). Når du tilføjer nuller, skal du altid tilføje dem i den retning, du arbejder. Den endelige fordeling er 010 010, 110.

3. Brug oktalkonverteringstabellen til at konvertere tilbage fra oktal til binær. Du skal bruge bordet til at arbejde baglæns, fordi en enkel "3" giver dig ikke nok information til at udføre beregningen, medmindre du kender det oktale system godt og ønsker at overveje hver kombination. Du skal blot bruge følgende diagram til nemt at konvertere et oktalt ciffer til en sekvens af tre binære tal, og placer dem derefter side om side: