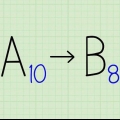Konvertering fra decimal til hexadecimal: 15 trin (med billeder)

Indhold

Konverteringer med små tal
Trin
- Metode 1 af 2: Intuitiv metode
- Metode 2 af 2: Hurtig metode (med hvile)
Tips

Hexadecimal er et talsystem med grundtallet seksten. Det betyder, at der er 16 symboler til at angive et tal, med A, B, C, D, E og F tilføjet til de sædvanlige ti cifre. Konvertering fra decimal til hexadecimal er sværere end omvendt. Tag dig tid til at lære dette, da det er nemmere at undgå fejl, når du først forstår, hvorfor konverteringen virker.

Konverteringer med små tal

Decimal	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Hexadecimal	0	1	2	3	4	5	6	7	8	9	-en	B	C	d	E	f

Trin

Metode 1 af 2: Intuitiv metode

1. Brug denne metode, hvis du er ny til hexadecimale tal. Af de to tilgange i denne artikel er dette den nemmeste for de fleste at følge. Hvis du allerede er bekendt med de forskellige baser, så prøv den hurtigere metode som angivet nedenfor.

Hvis du er helt uvant med hexadecimale tal, skal du først lære de grundlæggende begreber.

Billede med titlen Konverter fra decimal til hexadecimal Trin 2

2. Skriv potenserne af 16 ned. Hvert ciffer i det hexadecimale system repræsenterer en anden potens af 16, ligesom et decimaltal er en potens af 10. Denne liste over potenser på 16 vil være praktisk ved konvertering:

16 = 1.048.576

16 = 65.536

16 = 4.096

16 = 256

16 = 16

Hvis det decimaltal, du konverterer, er større end 1.048.576, beregn derefter de højere potenser af 16 og føj det til listen.

Billede med titlen Konverter fra decimal til hexadecimal Trin 3

3. Find den højeste potens af 16, der passer inden for decimaltallet. Skriv det decimaltal ned, du vil konvertere. Brug ovenstående liste som reference. Find den højeste potens af 16, der er mindre end decimaltallet.

Hvis du f.eks 495 konverter til hexadecimal, og vælg derefter 256 fra listen ovenfor.

Billede med titlen Konverter fra decimal til hexadecimal Trin 4

4. Divider decimaltallet med denne potens af 16. Stop ved det hele tal og ignorer hvert ciffer efter decimalkommaet i svaret.

I vores eksempel er 495 ÷ 256 = 1.93... , men vi er kun interesserede i hele nummeret 1.

Dit svar er det første ciffer i det hexadecimale tal. I dette tilfælde, da vi har divideret med 256, er 1-tallet tallet i stedet for "256-da."

Billede med titlen Konverter fra decimal til hexadecimal Trin 5

5. Find resten. Dette fortæller dig, hvad der er tilbage af det decimaltal, der skal konverteres. Sådan kan du regne det ud, ligesom med en lang division:

Gang dit sidste svar med divisor. I vores eksempel er 1 x 256 = 256. (Med andre ord repræsenterer 1`eren i vores hexadecimale tal 256 med grundtallet 10).

Træk dit svar fra udbyttet. 495 - 256 = 239.

Billede med titlen Konverter fra decimal til hexadecimal Trin 6

6. Divider resten med den næste højere potens af 16. Brug din liste over potenser på 16 igen som reference. Fortsæt sådan til mindst 16. Divider resten med denne værdi for at finde det næste ciffer i dit hexadecimale tal. (Hvis resten er mindre end dette tal, er det næste ciffer 0.)

239 ÷ 16 = 14. Igen ignorerer vi alle decimaler.

Dette er det andet ciffer i vores hexadecimale tal, den "16-og." Ethvert tal fra 0 til 15 kan repræsenteres som et enkelt hexadecimalt ciffer. Vi konverterer til den korrekte notation i slutningen af denne metode.

Billede med titlen Konverter fra decimal til hexadecimal Trin 7

7. Bestem resten igen. Som før skal du gange svaret med divisoren og trække det fra dividenden. Dette er resten, der stadig mangler at blive konverteret.

14 x 16 = 224.

239 - 224 = 15, så resten er 15.

Billede med titlen Konverter fra decimal til hexadecimal Trin 8

8. Gentag, indtil du har en rest på mindre end 16. Når resten er 0 til 15, kan det udtrykkes med et enkelt hexadecimalt ciffer. Skriv dette som det sidste tal.

Den sidste "figur" af vores hexadecimale tal er 15, i stedet for "enheder."

Billede med titlen Konverter fra decimal til hexadecimal Trin 9

9. Skriv dit svar i den rigtige notation. Du ved nu, hvad alle cifrene i dit hexadecimale tal er. Men indtil videre har vi kun skrevet dem i base ti. For at skrive hvert ciffer i den korrekte hexadecimale notation, konverter dem ved hjælp af denne vejledning:

Tallene 0 til 9 forbliver de samme.

10 = A; 11 = B; 12 = C; 13 = D; 14 = E; 15 = F

I vores eksempel ender vi med tallene (1)(14)(15). I korrekt notation bliver dette det hexadecimale tal 1EF.

Billede med titlen Konverter fra decimal til hexadecimal trin 10

10. Tjek dit arbejde. Det er nemt at tjekke dit svar, når du forstår, hvordan hexadecimale tal fungerer. Konverter hvert ciffer tilbage til decimalform, og gang dem med 16. potens for den grundposition. Her er, hvad vi skal gøre for vores eksempel:

1EF → (1)(14)(15)

Fra højre til venstre er 15 i 16 = 1. position. 15 x 1 = 15.

Det næste ciffer fra venstre er i 16 = 16. position. 14 x 16 = 224.

Det næste ciffer er i 16 = 256. position. 1 x 256 = 256.

Vi lægger dem alle sammen, 256 + 224 + 15 = 495, vores oprindelige nummer.

Metode 2 af 2: Hurtig metode (med hvile)

Billede med titlen Konverter fra decimal til hexadecimal trin 11

1. Divider decimaltallet med 16. Behandl denne division som en heltalsdivision. Man stopper med andre ord ved et svar med et helt tal, i stedet for at beregne decimaltallene.

Lad os være lidt mere ambitiøse omkring dette eksempel og decimaltallet 317.547 konvertere. Beregn 317.547 ÷ 16 = 19.846, og ignorer decimalerne.

Billede med titlen Konverter fra decimal til hexadecimal trin 12

2. Skriv resten i hexadecimal notation. Nu hvor du har divideret tallet med 16, er resten den del, der ikke længere passer til positionen for 16`erne eller højere. Derfor skal resten komme til enhedernes position, det sidst cifferet i det hexadecimale tal.

For at finde resten skal du gange svaret med divisoren og derefter trække resultatet fra dividenden. I vores eksempel, 317.547 - (19.846 x 16) = 11.

Konverter cifferet til hexadecimalt format ved hjælp af den lille talkonverteringstabel øverst på denne artikelside. 11 omgange B i vores eksempel.

Billede med titlen Konverter fra decimal til hexadecimal trin 13

3. Gentag denne proces med kvotienten. Du konverterede resten til et hexadecimalt ciffer. For at fortsætte med at konvertere kvotienten skal du dividere den igen med 16. Resten er det næstsidste ciffer i det hexadecimale tal. Dette fungerer med samme logik som ovenfor: det oprindelige tal er nu divideret med (16 x 16 =) 256, så resten er den del af tallet, der passer til 256`ernes position. Vi kender allerede enhederne, resten skal være i 16`ernes plads.

I vores eksempel, 19.846 / 16 = 1.240.

resten = 19.846 - (1.240 x 16) = 6. Dette er det næstsidste ciffer i vores hexadecimale tal.

Billede med titlen Konverter fra decimal til hexadecimal trin 14

4. Gentag indtil du får en kvotient på mindre end 16. Glem ikke at konvertere en rest fra 10 til 15 i hexadecimalt format. Bemærk eventuel hvile undervejs. Den sidste kvotient (mindre end 16) er det første ciffer i dit nummer. Vi fortsætter med eksemplet:

Tag den sidste kvotient og divider den igen med 16. 1.240 / 16 = 77 resterende 8.

77 / 16 = 4 resten 13 = d.

4 < 16, altså 4 er det første ciffer.

Billede med titlen Konverter fra decimal til hexadecimal trin 15

5. Afslut nummeret. Som før nævnt bestemmer du hvert ciffer i det hexadecimale tal fra højre mod venstre. Tjek dit arbejde for at sikre dig, at du har skrevet dem i den rigtige rækkefølge.

Vores sidste svar er 4D86B.

For at kontrollere dit arbejde skal du konvertere hvert ciffer tilbage til decimaltallet, ganget med 16 potenser, og lægge resultaterne sammen. (4 x 16) + (13 x 16) + (8 x 16) + (6 x 16) + (11 x 1) = 317.547, vores oprindelige decimaltal.

Tips

For at undgå forvirring ved brug af de forskellige numeriske systemer, kan du skrive basen som et underskrift. For eksempel 512₁₀ er da "512 med base 10," et almindeligt decimaltal. 512₁₆ midler "512 med base 16," svarende til decimaltallet 1.298₁₀.