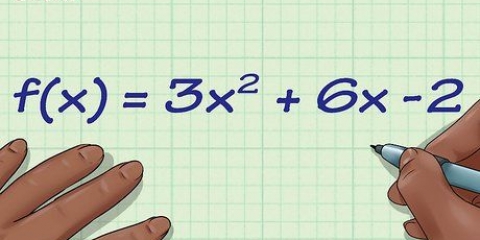Sådan tegner du en funktion: 10 trin (med billeder)

Indhold

Trin
Tips

Som en graf ser en andengradsligning ax + bx + c, også enhver skrevet soma(x - h) + k, ligner en glat U-formet kurve. Det er det, vi kalder en parabel. At tegne en andengradsligning indebærer at finde toppunktet, retningen og ofte skæringspunkter med x-aksen og y-aksen. Ved den relativt simple andengradsligning kan det også være tilstrækkeligt at indtaste en række værdier for x for at angive disse punkter i koordinatsystemet, hvorefter parablen kan tegnes. Fortsæt til trin 1 for at komme i gang.

Trin

1. Bestem, hvilken slags andengradsligning du har. Dette kan skrives på to måder: standardnotationen og toppunktsnotationen (en anden måde at skrive kvadratrodsformlen på). Du kan bruge begge dele til at lave en graf af en andengradsligning, men denne proces er lidt anderledes i begge tilfælde. Normalt vil du støde på standardformularen, men det skader bestemt ikke at lære at bruge begge former. De to former for en andengradsligning er:

Standardformen. Her skrives andengradsligningen som: f(x) = ax + bx + c hvor a, b og c er reelle tal og a ikke er lig nul.

To eksempler på standard andengradsligninger: f(x) = x + 2x + 1 og f(x) = 9x + 10x -8.

Topformen. Her skrives andengradsligningen som: f(x) = a(x - h) + k hvor a, h og k er reelle tal og a ikke er lig nul. Denne form kaldes toppunkt, fordi h og k refererer direkte til din parabels toppunkt i punktet (h,k).

To eksempler på ligninger i toppunktsform er f(x) = 9(x - 4) + 18 og -3(x - 5) + 1

For at kunne lave en graf af disse ligninger, bestemmer vi først toppen (h,k) af grafen. I standardligningen kan du finde dette via: h = -b/2a og k = f(h), mens det allerede er givet i toppunktsform, fordi h og k forekommer i ligningen.

Billede med titlen Graph a Quadratic Equation Trin 2

2. Bestem dine variabler. For at løse en andengradsligning er det normalt nødvendigt at bestemme variablerne a, b og c (eller a, h og k). Et almindeligt problem vil give dig en andengradsligning i standardformen, men toppunktsnotationen kan også forekomme.

For eksempel: standardfunktionen f(x) = 2x +16x + 39. Her har vi a = 2, b = 16 og c = 39.

I toppunktsnotation: f(x) = 4(x - 5) + 12. Her har vi a = 4, h = 5 og k = 12.

Billede med titlen Grafér en kvadratisk ligning Trin 3

3. Beregn h. I topnotationen er værdien af h allerede givet, men i standardnotationen er denne værdi endnu ikke beregnet. Husk, at for standardligningen er h = -b/2a.

Eksempel 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). Ved at løse dette ser vi, at h = -4.

Eksempel 2. (f(x) = 4(x - 5) + 12), ser vi straks, at h = 5.

Billede med titlen Graph a Quadratic Equation Trin 4

4. Beregn k. Som med h er k allerede kendt for ligninger i topformen. For ligninger i standardnotation skal du huske, at k = f(h). Med andre ord kan du finde k ved at erstatte hver variabel x med værdien af h.

Vi har for eksempel set 1, at h = -4. For at finde k løser vi denne ligning ved at indsætte denne værdi af h i ligningen for variablen x:

k = 2(-4) + 16(-4) + 39.

k = 2(16) - 64 + 39.

k = 32 - 64 + 39 = 7

Fra eksempel 2 ved vi, at værdien af k er lig med 12, uden behov for en beregning.

Billede med titlen Graph a Quadratic Equation Trin 5

5. Tegn toppen eller bunden af grafen. Kammen eller dalen af din parabel er punktet (h, k) - h repræsenterer x-koordinaten og k repræsenterer y-koordinaten. Toppen er midten af din parabel - det højeste eller laveste punkt, toppen eller dalen, af en graf i form af en "DU" eller omvendt. At kunne bestemme toppunktet på en parabel er en væsentlig del af at kunne tegne en korrekt graf – ofte er bestemmelse af en parabels toppunkt en del af et matematikopgave i skolen.

I eksempel 1 er toppen af grafen (-4,7). Tegn punktet på din graf, og sørg for at navngive koordinaterne korrekt.

I eksempel 2 er toppen (5,12). Så fra punktet (0,0) går du 5 pladser til højre og derefter 12 op.

Billede med titlen Grafér en kvadratisk ligning Trin 6

6. Tegn symmetriaksen for parablen. Symmetriaksen for en parabel er den linje, der skærer figuren i midten og deler den nøjagtigt i to. Den ene side af grafen er spejlet langs denne linje i den anden side af grafen. For andengradsligninger af enten formen ax + bx + c eller a(x - h) + k er denne akse linjen parallel med y-aksen, der går gennem parablens toppunkt.

I tilfælde af eksempel 1 er symmetriaksen linjen parallel med y-aksen og går gennem punktet (-4, 7). Selvom det ikke er en del af selve parablen, kan en let fremhævelse af denne guide vise dig, hvor symmetrisk parablens kurve er.

Billede med titlen Graph a Quadratic Equation Trin 7

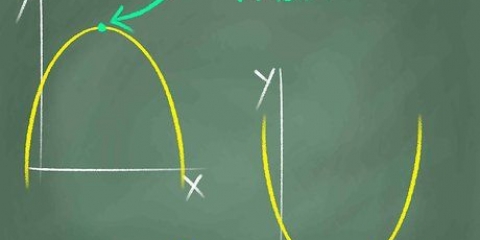
7. Bestem retningen af parablen. Efter du har fundet ud af, hvad toppen af parablen er, er det nødvendigt at vide, om du har med en bjergparabel eller en dalparabel at gøre, altså om åbningen er i bunden eller i toppen. Heldigvis er dette meget enkelt. hvis "-en" positivt, at du har at gøre med en dalparabel; er "-en" negativ, så er det en bjergparabel (med åbningen i bunden)

I eksempel 1 har vi at gøre med funktionen (f(x) = 2x +16x + 39), og dette er derfor en dalparabel, fordi a = 2 (positiv).

I eksempel 2 har vi at gøre med funktionen f(x) = 4(x - 5) + 12), og dette er også en dalparabel, fordi a = 4 (positiv).

Billede med titlen Graph a Quadratic Equation Trin 8

8. Bestem om nødvendigt parablens skæringspunkter. Ofte bliver du i matematikopgaver bedt om at angive skæringspunkterne mellem parablen og x-aksen (disse er "nul", -en eller to punkter, hvor parablen skærer eller rører x-aksen). Selvom de ikke bliver bedt om, er disse punkter meget vigtige for at kunne tegne en nøjagtig graf. Men ikke alle parabler skærer x-aksen. Hvis du har at gøre med en dalparabel, og dalpunktet er over x-aksen eller, i tilfælde af en bjergparabel, lige under x-aksen, så er der simpelthen ingen skæringspunkter at finde. Hvis ja, brug en af følgende metoder:

Bestem at f(x) = 0 og løs ligningen. Denne metode kan fungere til simple andengradsligninger, især i vertexformen, men du vil opdage, at det bliver sværere og sværere, efterhånden som funktionerne bliver mere komplekse. Nedenfor er et par eksempler.

f(x) = 4(x - 12)

0 = 4(x - 12) - 4

4 = 4(x - 12)

1 = (x - 12)

SqRt(1) = (x - 12)

+/- 1 = x -12. x = 11 og 13 er skæringspunkterne med parablens x-akse.

Faktorer ligningen. Nogle ligninger på formen ax + bx + c kan let omskrives som (dx + e)(fx +g), hvor dx × fx = ax, (dx × g + fx × e) = bx og e × g = c. I dette tilfælde er x-skæringspunkterne værdierne af x, hvor hvert led inden for parentesen bliver 0. For eksempel:

x + 2x + 1

= (x + 1)(x + 1)

I dette tilfælde er skæringspunktet lig med -1, fordi det, når det udfyldes med begge faktorer, giver nul.

Brug abc-formlen. Hvis det ikke er nemt at finde ud af skæringspunkterne eller faktorisere ligningen, skal du bruge "abc formel" som er specielt beregnet til dette. Antag en ligning på formen ax + bx + c. Indtast derefter værdierne af a, b og c i formlen x = (-b +/- SqRt(b - 4ac))/2a. Bemærk, at dette ofte giver dig to svar for x, hvilket er fint - det betyder bare, at din parabel har to skæringspunkter med x-aksen. Her er et eksempel:

-Indsæt 5x + 1x + 10 i ligningen som følger:

x = (-1 +/- SqRt(1 - 4(-5)(10)))/2(-5)

x = (-1 +/- SqRt(1 + 200))/-10

x = (-1 +/- SqRt(201))/-10

x = (-1 +/- 14,18)/-10

x = (13,18/-10) og (-15,18/-10). Skæringspunkterne mellem parablen og x-aksen er cirka x = -1.318 og 1.518

Som i eksempel 1 med ligningen 2x + 16x + 39, vil dette se sådan ud:

x = (-16 +/- SqRt(16 - 4(2)(39))))/2(2)

x = (-16 +/- SqRt(256 - 312))/4

x = (-16 +/- SqRt(-56)/-10

Da det ikke er muligt at finde kvadratroden af et negativt tal, ved vi, at der ikke findes nogen skæringspunkter med x-aksen for denne parabel.

Billede med titlen Graph a Quadratic Equation Trin 9

9. Bestem eventuelt skæringspunktet mellem parablen og y-aksen. Det er ofte ikke nødvendigt, men nogle gange påkrævet at finde dette skæringspunkt, for eksempel til en matematikopgave. Dette er ret nemt - indstil værdien af x til 0 og løs ligningen for f(x) eller y, som giver dig y-værdien af det punkt, hvor parablen skærer y-aksen. Forskellen med skæringerne gennem x-aksen er, at der med y-aksen altid kun er ét skæringspunkt. Bemærk – for standardligninger er skæringen med y-aksen ved y = c.

For eksempel ved vi, at vores andengradsligning 2x + 16x + 39 har et skæringspunkt y = 39, men vi kan også finde dette som følger:

f(x) = 2x + 16x + 39

f(x) = 2(0) + 16(0) + 39

f(x) = 39. Skæringspunktet mellem parablen og y-aksen: y = 39. Som angivet ovenfor kan vi nemt læse skæringspunktet, fordi y = c.

Ligningen 4(x - 5) + 12 har et skæringspunkt med y-aksen, der kan findes som følger:

f(x) = 4(x - 5) + 12

f(x) = 4(0 - 5) + 12

f(x) = 4(-5) + 12

f(x) = 4(25) + 12

f(x) = 112. Skæringspunktet med y-aksen: y = 112.

Billede med titlen Graph a Quadratic Equation Trin 10

10. Hvis du finder det nødvendigt, skal du først tegne ekstra point og derefter hele grafen. Du skulle nu have en top eller dal, en retning, skæringspunkter med x-aksen og muligvis med y-aksen i din ligning. Fra dette punkt kan du prøve at tegne parablen ved hjælp af disse punkter, eller du kan prøve at finde flere punkter for at gøre grafen mere nøjagtig. Den nemmeste måde at gøre dette på er blot ved at udfylde et antal x-værdier, hvilket returnerer et antal y-værdier. Du vil ofte blive bedt (af læreren) om først at udregne et antal point, før du kan tegne parablen.

Lad os se igen på ligningen x + 2x + 1. Vi ved allerede, at det eneste skæringspunkt med x-aksen er (-1,0). Da den kun tangerer x-aksen på dette punkt, kan vi udlede, at grafens toppunkt er lig med dette punkt. Indtil videre har vi kun ét punkt i denne parabel – ikke nær nok til at kunne tegne en graf. Lad os finde et par punkter mere for at sikre, at vi har flere værdier.

Lad os prøve at finde de y-værdier, der er forbundet med følgende x-værdier: 0, 1, -2 og -3.

x=0: f(x) = (0) + 2(0) + 1 = 1. Så er pointen (0,1).

x=1: f(x) = (1) + 2(1) + 1 = 4. Så er pointen (1,4).

x=-2: f(x) = (-2) + 2(-2) + 1 = 1. Så er pointen (-2,1).

x=-3: f(x) = (-3) + 2(-3) + 1 = 4. Så er pointen (-3,4).

Placer disse punkter i grafen og tegn din parabel. Bemærk at parablen er fuldstændig symmetrisk - kender du punkterne på den ene side af grafen, kan du som regel spare dig selv for en masse arbejde ved at bruge disse punkter til at finde punkterne på den anden side af symmetriaksen.

Tips

Afrund eventuelt tal eller brug brøker. Dette kan hjælpe med at vise en graf korrekt.
Bemærk, at hvis, for funktionen f(x) = ax + bx + c, b eller c er lig nul, vil disse led forsvinde. For eksempel er 12x + 0x + 6 lig med 12x + 6, fordi 0x er lig med 0.