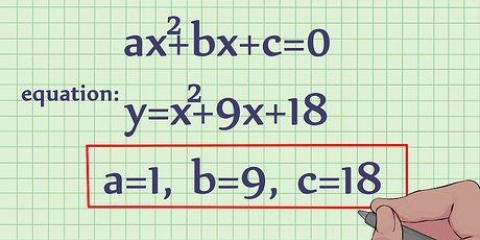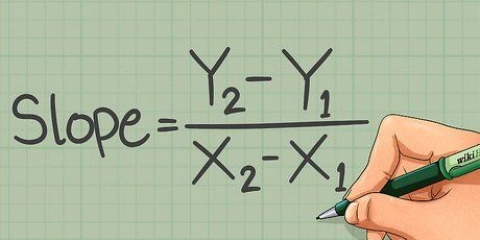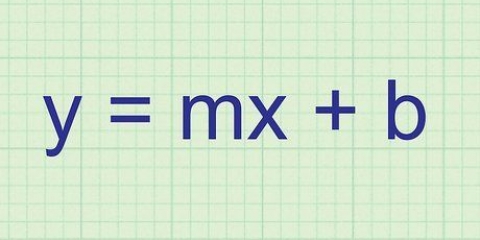Konstanten b er defineret som `skæringspunktet med y-aksen` Dette er det punkt, hvor linjen skærer y-aksen.
Begge x hvis y er variable. Du kan f.eks. angive en værdi på x løse, hvis du y kender, såvel som værdierne m og b. Det x er dog aldrig kun én værdi: værdien ændres, når du bevæger dig op eller ned i grafen.

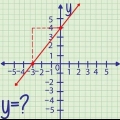
For eksempel tager vi ligningen y = 1/4x + 5. Siden sidste ciffer b er, det ved vi b er lig med 5. Flyt 5 punkter op på y-aksen og marker punktet. Det er her din lige linje krydser y-aksen.

Det første tal (tælleren) er øge fra y over x. Dette er hvor langt linjen stiger (bevæger sig lodret).
Det andet tal (nævneren) er x i y over x. Dette er hvor langt linjen bevæger sig (skifter vandret).
For eksempel:
En hældning på 4/1 øger 4 point for hver vandret forskydning på 1 point. En hældning på -2/1 falder 2 point for hver vandret forskydning på 1 point. En hældning på 1/5 øger 1 point for hver vandret forskydning på 5 point. 
For eksempel, i grafen ovenfor kan du se, at for hvert punkt, som linjen øges, flytter den fire punkter til højre. Det skyldes, at linjens hældning er ¼ (y/x). Du fortsætter med at forlænge linjen langs begge sider ved hjælp af y over x. Mens positive skråninger stiger, falder negative skråninger. En hældning på -1/4, for eksempel, falder et punkt for hver fire punkter, den skifter til højre. 
Tegning af en lineær ligning
Ved ikke, hvordan man tegner en lineær ligning uden en lommeregner? Heldigvis er det ret simpelt at tegne en lineær ligning! Du skal bare vide et par ting om din ligning, og du er klar til at gå. Lad os begynde!
Trin

1. Sørg for, at det er en lineær ligning af formen y = mx + b. Dette kaldes y-skæringspunktet og er sandsynligvis den enkleste graf i en lineær ligning. Værdierne i ligningen behøver ikke at være heltal. Du ser ofte en ligning som: y = 1/4x + 5, hvor 1/4 er lig m og 5 på b.
- Konstanten m kaldes `hældningen` eller `hældningen`. Bakken defineres som ændring i y i forhold til ændringen i x.




2. Tegn tallet b på y-aksen. Konstanten b er altid et rationelt tal. hvad nummeret b find også dets ækvivalent på y-aksen og tegn dets nummer på det sted på den lodrette akse.


3. Bevæge sig m at være i et brud. Nummeret x er ofte allerede en brøk, så du behøver ikke konvertere den. Men hvis ikke, konverter den ved blot at ændre værdien af m som tæller og 1 som nævner.



4. Begynd at forlænge linjen fra b ved hjælp af den velkendte skråning. Start ved værdien for b: vi ved, at ligningen passerer dette punkt. Forlæng linjen ved at bruge hældningen til at bestemme de følgende punkter i ligningen.

5. Fortsæt med at forlænge linjen (ved hjælp af en lineal og brug af hældningen m som guide. Forlæng linjen langs begge sider (til det uendelige), og du er færdig med at tegne linjen. Ret nemt, ikke sandt?
Artikler om emnet "Tegning af en lineær ligning"
Оцените, пожалуйста статью
Populær