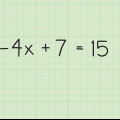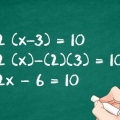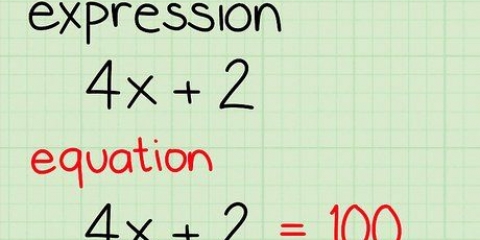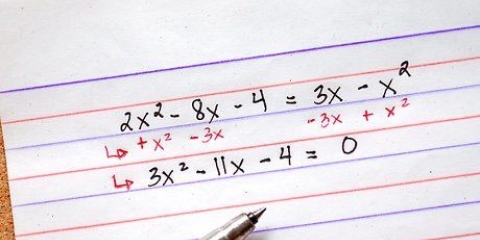4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 x = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2 x 16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6 x 2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

√(2x+9) - 5 + 5 = 0 + 5 √(2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

√(2x+9) - 5 = 0 √(2(8)+9) - 5 = 0 √(16+9) - 5 = 0 √(25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 x = -4 
(For x = 3): |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (for x = -4): |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Løs x i en ligning
Indhold
Der er flere måder at løse x i en ligning på, uanset om du arbejder med eksponenter og rødder eller blot skal dividere eller gange. Uanset hvilken metode du bruger, bør du altid finde en måde at isolere x fra den ene side af ligningen, så du kan beregne værdien. Sådan gør du det:
Trin
Metode 1 af 5: Brug af en almindelig lineær ligning

1. Skriv problemet ned. Her er opgaven:
- 2(x+3) + 9 - 5 = 32

2. Udregn eksponenten. Husk rækkefølgen af operationer: HMVDOA, som står for Parentheses, Exponentiation, Division/Multiply, Addition/Subtraction. I dette tilfælde kan du ikke regne ud, hvad der står i parentes først, fordi x`et hører til det, så du starter med potensen 2. 2 = 4

3. Regn multiplikationen ud. Gang 4 med (x+3). Sådan gør du:

4. Regn nu addition og subtraktion ud. Du skal blot tilføje eller trække de resterende tal fra. Sådan gør du:

5. Isoler variablen. Det gør du ved at dividere begge sider af ligningen med 4 for at finde x. 4x/4 = x og 16/4 = 4, så x = 4.

6. Tjek din beregning. Sæt x = 4 tilbage i den oprindelige ligning for at sikre, at den er korrekt. Sådan gør du:
Metode 2 af 5: Med eksponentiering

1. Skriv problemet ned. Lad os antage, at du arbejder på et problem, hvor x-leddet også indeholder en eksponent:
- 2x + 12 = 44

2. Isoler udtrykket med eksponenten. Den første ting du skal gøre nu er at kombinere ens udtryk, så alle konstanterne er på højre side af ligningen, mens udtrykket med eksponenten er til venstre. Træk blot 12 fra begge sider. Sådan gør du:

3. Isoler variablen med eksponenten ved at dividere begge sider med koefficienten for x-leddet. I dette tilfælde er 2 x-koefficienten, hvilket betyder, at begge sider skal divideres med 2 for at eliminere den. Sådan gør du:

4. Tag kvadratroden af hver side af ligningen. Ved at beregne kvadratroden af x står du tilbage med x til venstre og kvadratroden af 16,4 til højre. Så x = 4.

5. Tjek din beregning. Sæt x = 4 tilbage i den oprindelige ligning for at sikre, at den er korrekt. Sådan gør du:
Metode 3 af 5: Brug brøker

1. Skriv problemet ned. Lad os antage, at du har at gøre med følgende problem:
- (x + 3)/6 = 2/3

2. Cross Multiplikér. For at gange på kryds og tværs skal du gange nævneren for hver brøk gange tælleren for den anden brøk. Så gang 6 (den første nævner) med 2 (den anden tæller) for at få 12 på højre side af ligningen.Gang derefter 3 (den anden nævner) med x + 3 (den første tæller), for at få 3 x + 9 til venstre for ligningen. Sådan kommer det til at se ud:

3. Kombiner lignende udtryk. Kombiner konstanterne i ligningen ved at trække 9 fra begge sider af ligningen. Her er hvad du skal gøre:

4. Isoler x ved at dividere hvert led med x-koefficienten. Bare divider 3x og 9 med 3, koefficienten af x, og løs for x. 3x/3 = x og 3/3 = 1, så du står tilbage med x = 1.

5. Tjek din beregning. For at kontrollere dit arbejde skal du indsætte x tilbage i den oprindelige ligning for at sikre dig, at den er korrekt. Her er hvad du skal gøre:
Metode 4 af 5: Brug af rodtegn

1. Skriv problemet ned. Lad os antage, at du løser x i følgende problem:
- √(2x+9) - 5 = 0

2. Isoler kvadratroden. Du skal isolere kvadratrodsdelen af ligningen til venstre for ligningen, før du kan fortsætte. Så du tilføjer 5 til begge sider af ligningen. Sådan gør du:

3. Tegn kvadratroden af begge sider. Ligesom du dividerer begge sider af en ligning med koefficienten ganget med x, skal du også tage kvadratroden af begge sider af en ligning, hvis x er under radikaltegnet. Dette fjerner radikalet fra ligningen. Sådan gør du:

4. Kombiner lignende udtryk. Kombiner lige led ved at trække 9 fra begge sider af ligningen, så alle konstanter er til højre, mens x forbliver til venstre. Her er hvad du skal gøre:

5. Isoler variablen. Den sidste ting at gøre for at løse for x er at isolere variablen ved at dividere begge sider af ligningen med 2, koefficienten for x-leddet. 2x/2 = x og 16/2 = 8, så du står tilbage med x = 8.

6. Tjek din beregning. Indtast 8 i ligningen igen for x for at kontrollere, at din udregning er korrekt:
Metode 5 af 5: Brug den absolutte værdi

1. Skriv problemet ned. Lad os antage, at du prøver at løse x i følgende problem:
- |4x +2| - 6 = 8

2. Isoler den absolutte værdi. Den første ting at gøre er at kombinere ens udtryk og isolere den absolutte værdi. I dette tilfælde kan du gøre det ved at tilføje 6 til begge sider af ligningen. Sådan gør du:

3. Fjern den absolutte værdi og løs ligningen. Dette er det første og nemmeste skridt. Du skal nu løse x to gange, hver gang du arbejder med en absolut værdi. Sådan gør du det første gang:

4. Fjern den absolutte værdi og skift fortegnet for vilkårene på den anden side af lighedstegnet, før du fortsætter med at løse. Gør nu dette igen, denne gang gør den venstre del af ligningen lig med -14 i stedet for 14. Sådan gør du:

5. Tjek din beregning. Nu hvor du ved, at x = (3, -4), skal du bare erstatte begge tal tilbage i ligningen for at sikre dig, at det er rigtigt. Sådan gør du:
Tips
- For at kontrollere dit arbejde skal du indtaste værdien af x tilbage i den oprindelige ligning og løse for det.
- Rødder er en anden måde at repræsentere eksponenter på.Kvadratroden af x = x^1/2.
Artikler om emnet "Løs x i en ligning"
Оцените, пожалуйста статью
Populær