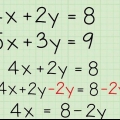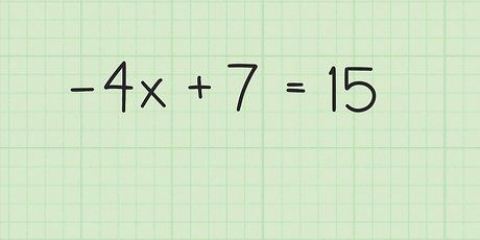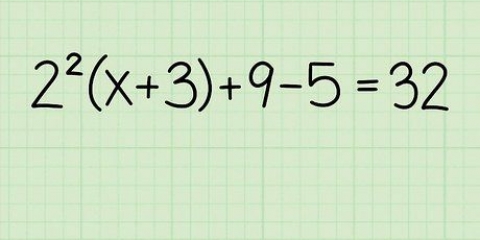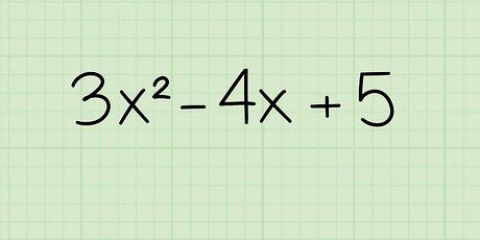3x + 5 + 4x - x + 2x + 9 = 3x - x + 4x + 2x + 5 + 9 = 2x + 6x + 14 
3x + 15 = 9x + 30 Du kan se, at hver koefficient er delelig med 3. Eliminer tallet 3 ved at dividere hvert led med 3 for at forenkle ligningen. 3x/3 + 15/3 = 9x/3 + 30/3 = x + 5 = 3x + 10 
(3 + 5) x 10 + 4 Først operationerne i parentes: = (8) x 10 + 4 Så skal vi hæve magten: = 64 x 10 + 4 Derefter multiplikationen: = 640 + 4 Og til sidst tilføjer vi: = 644 
5x + 15 = 65 = 5x/5 + 15/5 = 65/5 = x + 3 = 13 = x = 10 

2x + 12 = 44 Træk først 12 fra begge sider. 2x + 12 -12 = 44 -12 = 2x = 32 Divider nu begge sider med 2. 2x/2 = 32/2 = x = 16 Løs ved at tage kvadratroden af begge sider, for det gør x lig med x. √x = √16 = Giv begge svar: x = 4, -4 
(x + 3)/6 = 2/3 Først skal du gange på kryds og tværs for at slippe af med brøken. Gang tælleren for en brøk med nævneren af den anden brøk. (x + 3) x 3 = 2 x 6 = 3x + 9 = 12 Så kombinerer du lige vilkår. Kombiner de konstante led 9 og 12 ved at trække 9 fra begge sider. 3x + 9 - 9 = 12 - 9 = 3x = 3 Isoler variablen x ved at dividere begge sider med 3 og du har svaret. 3x/3 = 3/3 = x = 1 
√(2x+9) - 5 = 0 Flyt først alt, der ikke er under radikalet, til den anden side af ligningen: √(2x+9) = 5 Derefter firkanter begge sider for at fjerne radikalet: (√(2x+9)) = 5 = 2x + 9 = 25 Nu kan du løse ligningen som normalt ved at kombinere konstanterne og isolere variablen: 2x = 25 - 9 = 2x = 16 x = 8 
Sådan regner du ud for den absolutte værdi ved at isolere den absolutte værdi og derefter fjerne den: |4x +2| - 6 = 8 = |4x +2| = 8 + 6 = |4x +2| = 14 = 4x + 2 = 14 = 4x = 12 x = 3 Løs nu dette igen ved at invertere fortegnet for udtrykket på den anden side af ligningen, efter at du har isoleret den absolutte værdi: |4x +2| = 14 = 4x + 2 = -14 4x = -14 -2 4x = -16 4x/4 = -16/4 = x = -4 Giv nu begge svar: x = -4, 3
Løsning af et algebraisk udtryk
Et algebraisk udtryk er et matematisk udtryk, der indeholder tal og/eller variable. Selvom det ikke kan løses, fordi det ikke indeholder et lighedstegn (=), kan det forenkles. Det kan du dog løse matematiske ligninger, indeholdende algebraiske udtryk adskilt af et lighedstegn. Hvis du vil mestre dette matematiske koncept, så læs videre til trin 1 for at komme i gang.
Trin
Del 1 af 2: Forstå det grundlæggende

1. Forstå forskellen mellem et algebraisk udtryk og en algebraisk ligning. Et algebraisk udtryk er et matematisk udtryk, der indeholder tal og/eller variable. Det indeholder ikke et lighedstegn og kan ikke løses. En algebraisk ligning kan dog løses og involverer en række algebraiske udtryk adskilt af et lighedstegn. Her er nogle eksempler:
- Algebraisk udtryk: 4x + 2
- Algebraisk ligning: 4x + 2 = 100

2. Lær, hvordan du kombinerer lignende udtryk. At kombinere ens udtryk betyder simpelthen at tilføje (eller trække fra) vilkårene i samme grad. Det betyder, at alle x-led kan kombineres med andre x-led, alle x-led kan kombineres med x-led og alle konstanter (tal, der ikke er knyttet til variable, såsom 8 eller 5) kan også lægges sammen, eller kombineres med hinanden. Her er et eksempel:

3. Lær, hvordan du faktoriserer et tal. Hvis du har at gøre med en algebraisk ligning, hvilket betyder, at der er et udtryk på hver side af et lighedstegn, kan du forenkle dette ved at fjerne det almindelige udtryk. Se på koefficienterne for alle betingelserne (tallene før variablerne eller konstanterne) og se, om der er et tal, du kan "arbejde væk" ved at dividere hvert led med det tal. Hvis du kan gøre dette, så har du forenklet ligningen, og du er på vej til at løse den. Sådan fungerer det:

4. Kend rækkefølgen af operationer. Rækkefølgen af operationer, også kendt som den mnemoniske `How To Get Rid Of Die Insufficients`, angiver den rækkefølge, du skal udføre de forskellige matematiske operationer i. Rækkefølgen er: Parenteser, Eksponentiering, Rooting, Multiplikation, Division, Addition og Subtraktion. Her er et eksempel på, hvordan rækkefølgen af operationer fungerer:

5. Lær at isolere en variabel. Hvis du vil løse en algebraisk ligning, er dit mål at få variablen, ofte kendt som x, på den ene side af ligningen, og de konstante led på den anden side af ligningen. Du kan isolere x ved at dividere, gange, addere, subtrahere, bestemme kvadratroden eller andre operationer. Når du har isoleret x, kan du begynde at løse det. Sådan gør du:
Del 2 af 2: Løsning af en algebraisk ligning

1. Løs en simpel lineær algebraisk ligning. En lineær algebraisk ligning er fin og enkel, idet den kun bruger førstegradskonstanter og variabler (ingen potenser eller anden kompleksitet). For at løse dette skal du bare gange, dividere, addere eller subtrahere efter behov, for at isolere variablen og løse for `x`. Sådan gør du:
- 4x + 16 = 25 -3x =
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16 =
- 7x = 9
- 7x/7 = 9/7 =
- x = 9/7

2. Løs en algebraisk ligning med potenser (eksponenter). Hvis ligningen har potenser, så skal du bare finde en måde at isolere potensen på den ene side af ligningen og derefter løse den ved at "fjerne" potensen ved at finde kvadratroden af både potensen og konstant på den anden side af ligningen. Sådan gør du:

3. Løs et algebraisk udtryk med brøker. For at løse et algebraisk udtryk, der indeholder brøker, skal du krydse gange brøkerne, kombinere lignende udtryk og derefter isolere variablen. Sådan gør du:

4. Løs et algebraisk udtryk. Hvis du har at gøre med et algebraisk udtryk med radikaler, er alt du skal gøre at finde en måde at kvadre begge sider, så du kan eliminere radikalen for at løse variablen. Sådan gør du:

5. Løs et algebraisk udtryk, der indeholder en absolut værdi. Den absolutte værdi af et tal repræsenterer dets værdi, uanset om det er positivt eller negativt; den absolutte værdi er altid positiv. Så for eksempel er den absolutte værdi af -3 (også kendt som |3|) kun 3. For at finde den absolutte værdi skal du isolere den absolutte værdi og derefter løse for x to gange (både for x, hvor den absolutte værdi blot fjernes, og for x, hvor led på den anden side af lighedstegnet har skiftet fortegn, fra positivt til negativt og omvendt). Dette går sådan her:
Tips
- For at dobbelttjekke dit svar kan du gå til wolfram-alpha.dk gå. Der kan du få svaret, ofte vist i de to trin.
- Når du er færdig, skal du erstatte variablen med svaret, og derefter løse summen for at se, om den er korrekt. Hvis ja, tillykke, du er færdig! Du har lige løst en algebraisk ligning!
- Graden af et polynomium er den højeste potens inden for termerne.
Artikler om emnet "Løsning af et algebraisk udtryk"
Оцените, пожалуйста статью
Populær