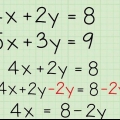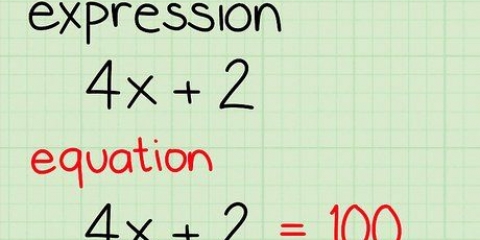Løsning af brøkligninger: 8 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Metode 1: Krydsmultiplikation
- Metode 2 af 2: Metode 2: Find det mindste fælles multiplum (LCM) af nævnerne
Tips

En rationel funktion er en brøk med en eller flere variable i tælleren eller nævneren. En rationel ligning er enhver ligning, der indeholder mindst ét rationelt udtryk. Ligesom regulære algebraiske ligninger kan rationelle udtryk løses ved at anvende den samme operation på begge sider af ligningen, indtil variablen er isoleret på den ene side af lighedstegnet. To specielle metoder, krydsmultiplikation og at finde det mindste fælles multiplum af nævnerne, er særligt nyttige til at isolere variable og løse rationelle ligninger.

Trin

Metode 1 af 2: Metode 1: Krydsmultiplikation

1. Omarranger om nødvendigt ligningen for at sikre, at der er en brøk på begge sider af lighedstegnet. Krydsmultiplikation er en hurtig metode til at løse rationelle ligninger. Desværre virker denne metode kun for rationelle ligninger, der har præcis ét rationelt udtryk eller brøk på begge sider af lighedstegnet. Hvis dette ikke er tilfældet i din ligning, så har du sandsynligvis brug for nogle algebraiske operationer for at få termerne på det rigtige sted.

For eksempel kan ligningen (x + 3)/4 - x/(-2) = 0 let konverteres til den korrekte form for krydsmultiplikation ved at lægge x/(-2) til begge sider af ligningen, så den bliver resultatet ser sådan ud: (x + 3)/4 = x/(-2).

Husk, at decimaler og heltal kan konverteres til brøker ved at give dem som nævner 1. (x + 3)/4 - 2.5 = 5 kan for eksempel omskrives som (x + 3)/4 = 7.5/1, som gør det muligt at anvende krydsmultiplikation.

Nogle rationelle ligninger kan ikke så let konverteres til den korrekte form. I disse tilfælde skal du bruge de metoder, der bruger det mindste fælles multiplum af nævnerne.

Billede med titlen Solve Rational Equations Trin 2

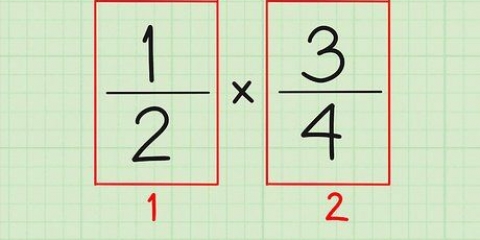
2. Cross Multiplikér. Krydsmultiplikation betyder simpelthen at gange tælleren for en brøk med nævneren af den anden og omvendt. Gang tælleren for brøken til venstre for lighedstegnet med brøken til højre. Gentag med tælleren til højre og nævneren af brøken til venstre.

Krydsmultiplikation fungerer efter almindelige algebraiske principper. Rationelle udtryk og andre brøker kan konverteres til almindelige tal ved at gange nævnerne. Krydsmultiplikation er dybest set en bekvem, forkortet måde at gange begge sider af ligningen med nævnerne af brøkerne. Tror du ikke på det? Prøv det - du vil se de samme resultater efter forenkling.

Billede med titlen Solve Rational Equations Trin 3

3. Gør de to produkter lige med hinanden. Efter krydsmultiplikationen står du tilbage med to produkter. Gør disse to led ens og forenkle dem for at efterlade de enkleste udtryk på begge sider af ligningen.

For eksempel, hvis (x+3)/4 = x/(-2) var dit oprindelige rationelle udtryk, så bliver det efter krydsmultiplikation lig med -2(x+3) = 4x. Dette kan muligvis omskrives til -2x - 6 = 4x.

Billede med titlen Løs rationelle ligninger Trin 4

4. Løs for variablen. Brug algebraiske operationer til at finde værdien af variablen i ligningen. Husk, at hvis x vises på begge sider af lighedstegnet, skal du tilføje eller trække et x-led fra for at sikre, at der kun er x-led på den ene side af lighedstegnet.

I vores eksempel er det muligt at dividere begge sider af ligningen med -2, hvilket giver usx+3 = -2x. At trække x fra begge sider af lighedstegnet giver os 3 = -3x. Og endelig ved at dividere begge sider med -3 får vi -1 = x, eller også x = -1. Nu har vi fundet x ved at løse vores rationelle ligning.

Metode 2 af 2: Metode 2: Find det mindste fælles multiplum (LCM) af nævnerne

Billede med titlen Løs rationelle ligninger Trin 5

1. Prøv at se, hvornår det er indlysende at finde det mindste fælles multiplum af nævnerne. Det mindste fælles multiplum (LCM) af nævnerne kan bruges til at forenkle rationelle ligninger, hvilket gør det muligt at finde værdierne af deres variabler. At finde en LCF er en god idé, hvis den rationelle ligning ikke let kan omskrives i en form, hvor der kun er en brøk eller et rationelt udtryk på hver side af lighedstegnet. Til løsning af rationelle ligninger med tre led eller flere er LCF`er et nyttigt værktøj. Men for at løse rationelle ligninger med kun to led er krydsmultiplikation ofte hurtigere.

Billede med titlen Solve Rational Equations Trin 6

2. Undersøg nævneren for hver brøk. Find det mindste tal, der er deleligt med en vilkårlig nævner. Dette er kgv af din ligning.

Nogle gange er det mindste fælles multiplum - det mindste tal, der er deleligt med hver af nævnerne - umiddelbart synligt. For eksempel, hvis dit udtryk ser ud som x/3 + 1/2 = (3x+1)/6, så er det let at se, at lcm skal være deleligt med 3, 2 og 6, så det er lig med 6.

Men oftere er LCF for en rationel ligning slet ikke umiddelbart klar. I disse tilfælde skal du prøve multipla af den største nævner, indtil du finder et tal, der inkluderer multipla af de andre, mindre nævnere. Ofte er LCF et produkt af to nævnere. Tag for eksempel ligningen x/8 + 2/6 = (x - 3)/9, hvor lcm er lig med 8*9 = 72.

Hvis en eller flere af nævnerne indeholder en variabel, er denne proces noget vanskeligere, men det er bestemt ikke umuligt. I de tilfælde er LCF et udtryk (med variabler), som alle nævnere passer fuldstændig ind i, ikke kun et enkelt tal. Som et eksempel er ligningen 5/(x-1) = 1/x + 2/(3x), hvor lcg er lig med 3x(x-1), fordi den er fuldt delelig med en hvilken som helst nævner – divideret med (x- 1 ) giver 3x, division med 3x giver (x-1) og division med x giver 3(x-1).

Billede med titlen Solve Rational Equations Trin 7

3. Gang hver brøk i den rationelle ligning med 1. At gange ethvert led med 1 kan virke meningsløst, men der er et trick her. 1 kan skrives som en brøk – f.eks. 2/2 og 3/3. Gang hver brøk i din rationelle ligning med 1, og skriv 1 hver gang tallet eller led ganget med hver nævner for at repræsentere LCF som en brøk.

I vores eksempel kan vi gange x/3 med 2/2 for at få 2x/6 og gange 1/2 med 3/3 for at få 3/6. 3x +1/6 har allerede et 6 (LCM) som nævner, så vi kan gange det med 1/1 eller bare lade være.

I vores eksempel med variabler i nævnerne er hele processen lidt mere kompliceret. Da lcc er lig med 3x(x-1), multiplicerer vi ethvert rationelt udtryk med en brøk, der giver 3x(x-1) som nævneren. Vi gange 5/(x-1) med (3x)/(3x), og det giver 5(3x)/(3x)(x-1), vi ganger 1/x med 3(x-1)/3(x) -1) og det giver 3(x-1)/3x(x-1) og vi gange 2/(3x) med (x-1)/(x-1) og det giver til sidst 2(x-1)/ 3x(x-1).

Billede med titlen Solve Rational Equations Trin 8

4. Forenkle og løse for x. Nu hvor hvert led i din rationelle ligning har den samme nævner, er det muligt at fjerne nævnerne fra ligningen og løse for tællere. Du skal bare gange begge sider af ligningen med lcg for at eliminere nævnerne, så du kun står tilbage med tællerne. Nu er det blevet en regulær ligning, som du kan løse for variablen ved at isolere den på den ene side af lighedstegnet.

I vores eksempel, efter at have ganget, ved at satse 1 som en brøk, får vi 2x/6 + 3/6 = (3x+1)/6. To brøker kan tilføjes, hvis de har samme nævner, så vi kan skrive denne ligning som (2x+3)/6 = (3x+1)/6 uden at ændre dens værdi. Multiplicer begge sider med 6 for at annullere nævnerne, hvilket efterlader os med 2x+3 = 3x+1. Her trækkes 1 fra begge sider for at få 2x+2 = 3x og trækkes 2x fra begge sider for at få 2 = x, som så også kan skrives som x = 2.

I vores eksempel med variable i nævnerne, ligningen efter at gange hvert led med "1" lig med 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). At gange hvert led med lcm gør det muligt at eliminere nævnerne, hvilket giver os 5(3x) = 3(x-1) + 2(x-1). Dette er yderligere uddybet som 15x = 3x - 3 + 2x -2, hvilket igen kan forenkles som 15x = x - 5. At trække x fra begge sider giver 14x = -5, hvilket kan forenkle det endelige svar til x = -5/14.

Tips

Når du har fundet værdien af variablen, skal du kontrollere dit svar ved at indsætte denne værdi i den oprindelige ligning. Når du har fået den rigtige værdi af variablen, burde du være i stand til at forenkle ligningen til en simpel, gyldig sætning, såsom 1 = 1.
Hver ligning kan skrives som et rationelt udtryk; bare sæt det som tæller over nævneren 1. Så ligningen x+3 kan skrives som (x+3)/1, begge har samme værdi.