Der er 4 grundlæggende trigonometriske ligninger: sin x = a; cos x = a tan x = a; tremmeseng x = a Løsning af de grundlæggende trigonometriske ligninger sker ved at studere de forskellige positioner af kurven x på den trigonometriske cirkel og ved at bruge en trigonometrisk omregningstabel (eller lommeregner). For fuldt ud at forstå, hvordan man løser disse og lignende grundlæggende trigonometriske ligninger, skal du læse følgende bog:"Trigonometri: Løsning af trigonometriske ligninger og uligheder" (Amazon E-bog 2010). Eksempel 1. Løs for sin x = 0,866. Omregningstabellen (eller lommeregneren) giver svaret: x = Pi/3. Den trigonometriske cirkel giver en anden kurve (2Pi/3) med samme værdi for sinus (0,866). Den trigonometriske cirkel giver også en uendelighed af svar kaldet udvidede svar. x1 = Pi/3 + 2k.Pi, og x2 = 2Pi/3.(Svar inden for en periode (0, 2Pi)) x1 = Pi/3 + 2k Pi, og x2 = 2Pi/3 + 2k Pi.(detaljerede svar). Eksempel 2. Løs: cos x = -1/2. Regnemaskiner giver x = 2 Pi/3. Den trigonometriske cirkel giver også x = -2Pi/3. x1 = 2Pi/3 + 2k.Pi, og x2 = - 2Pi/3.(Svar for punktum (0, 2Pi)) x1 = 2Pi/3 + 2k Pi, og x2 = -2Pi/3 + 2k.pi.(detaljerede svar) Eksempel 3. Løs: tan (x - Pi/4) = 0. x = Pi/4 ;(Svar) x = Pi/4 + k Pi;(Udvidet svar) Eksempel 4. Løs: tremmeseng 2x = 1.732. Lommeregnere og den trigonometriske cirkel giver: x = Pi/12 ;(Svar) x = Pi/12 + k Pi ;(detaljerede svar) 
For at konvertere en given trigonometrisk ligning til standard trigonometriske ligninger, skal du bruge standard algebraiske konverteringer (faktorisere, fælles faktor, polynomier...), definitioner og egenskaber ved trigonometriske funktioner og trigonometriske identiteter. Der er omkring 31, hvoraf 14 er trigonometriske identiteter, fra 19 til 31, også kaldet detransforme identiteter, fordi de bruges til konvertering af trigonometriske ligninger. Se ovenstående bog. Eksempel 5: Den trigonometriske ligning: sin x + sin 2x + sin 3x = 0 kan konverteres ved hjælp af trigonometriske identiteter til et produkt af grundlæggende trigonometriske ligninger: 4cos x*sin (3x/2)*cos (x/2) = 0. De grundlæggende trigonometriske ligninger, der skal løses, er: cos x = 0 ; sin(3x/2) = 0 ; og cos(x/2) = 0. 
Før du kan lære at løse trigonometriske ligninger, skal du vide, hvordan du hurtigt finder de kurver, hvis trigonometriske funktioner er kendte. Konverteringsværdier af kurver (eller vinkler) kan bestemmes med trigonometriske tabeller eller lommeregneren. Eksempel: Løs for cos x = 0.732. Lommeregneren giver løsningen x = 42,95 grader. Enhedscirklen giver andre kurver med samme værdi for cosinus. 
Du kan lave en graf for at illustrere løsningen til enhedscirklen. Endepunkterne for disse kurver består af almindelige polygoner på den trigonometriske cirkel. Nogle eksempler: Slutpunkterne for kurven x = Pi/3 + k.Pi/2 er en firkant på enhedscirklen. Kurverne for x = Pi/4 + k.Pi/3 er repræsenteret ved koordinaterne for en sekskant på enhedscirklen. 
Hvis den givne trigonometriske ligning kun indeholder én trigonometrisk funktion, løses den som en standard trigonometrisk ligning. Hvis den givne ligning indeholder to eller flere trigonometriske funktioner, er der 2 løsningsmetoder afhængigt af mulighederne for at konvertere ligningen. -en.Metode 1. Konverter den trigonometriske ligning til et produkt af formen: f(x).g(x) = 0 eller f(x).g(x).h(x) = 0, hvor f(x), g(x) og h(x) er grundlæggende trigonometriske ligninger. Eksempel 6. Løs: 2cos x + sin 2x = 0.(0 < x < 2Pi) Opløsning. Erstat sin 2x i ligningen ved at bruge identiteten: sin 2x = 2*sin x*cos x. cos x + 2*sin x*cos x = 2cos x*( sin x + 1)= 0. Løs derefter 2 trigonometriske standardfunktioner: cos x = 0, og (sin x + 1) = 0. Eksempel 7. Løs: cos x + cos 2x + cos 3x = 0.(0 < x < 2Pi) Løsning: Konverter dette til et produkt ved hjælp af de trigonometriske identiteter: cos 2x(2cos x + 1 ) = 0. Løs nu de 2 grundlæggende trigonometriske ligninger: cos 2x = 0, og (2cos x + 1) = 0. Eksempel 8. Løs: sin x - sin 3x = cos 2x.(0 < x < 2Pi) Løsning: Konverter dette til et produkt ved hjælp af de trigonometriske identiteter: -cos 2x*(2sin x + 1) = 0. Løs nu de 2 grundlæggende trigonometriske ligninger: cos 2x = 0, og (2sin x + 1) = 0. B.tilgang 2. Konverter den trigonometriske ligning til en trigonometrisk ligning med kun én unik trigonometrisk funktion som variabel. Der er nogle tips til, hvordan du vælger en passende variabel. Almindelige variabler er: sin x = t; cos x = t; cos 2x = t, tan x = t og tan (x/2) = t. Eksempel 9. Løs: 3sin^2 x - 2cos^2 x = 4sin x + 7(0 < x < 2Pi). Opløsning. I ligningen skal du erstatte (cos^2 x) med (1 - sin^2 x), og forenkle ligningen: 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Brug nu sin x = t. Ligningen bliver: 5t^2 - 4t - 9 = 0. Dette er en andengradsligning med 2 rødder: t1 = -1 og t2 = 9/5. Vi kan afvise den anden t2 fordi > 1. Løs nu for: t = sin = -1 --> x = 3Pi/2. Eksempel 10. Løs: tan x + 2 tan^2 x = barneseng x + 2. Opløsning. Brug tan x = t. Konverter den givne ligning til en ligning med t som variabel: (2t + 1)(t^2 - 1) = 0. Løs for t fra dette produkt, og løs derefter den trigonometriske standardligning tan x = t for x. 
Der er nogle få specielle trigonometriske ligninger, der kræver nogle specifikke konverteringer. Eksempler: a*sin x+ b*cos x = c ; a(sin x + cos x) + b*cos x*sin x = c ; a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0 
Alle trigonometriske funktioner er periodiske, hvilket betyder, at de vender tilbage til den samme værdi efter en rotation over en periode. Eksempler: Funktionen f(x) = sin x har 2Pi som punktum. Funktionen f(x) = tan x har Pi som punktum. Funktionen f(x) = sin 2x har Pi som punktum. Funktionen f(x) = cos (x/2) har 4Pi som punktum. Hvis perioden er angivet i øvelserne/testen, så skal du kun finde kurven(e) x indenfor denne periode. FORSIGTIG: Løsning af trigonometriske ligninger er vanskelig og fører ofte til fejl og fejl. Derfor bør svar kontrolleres omhyggeligt. Efter at have løst, kan du kontrollere svarene ved hjælp af en grafregner, for en direkte repræsentation af den givne trigonometriske ligning R(x) = 0. Svarene (som kvadratrod) er angivet i decimaler. Som et eksempel har Pi en værdi på 3,14
Løsning af trigonometriske ligninger
En trigonometrisk ligning er en ligning med en eller flere trigonometriske funktioner af den variable trigonometriske kurve x. At løse for x betyder at finde værdierne af de trigonometriske kurver, hvis trigonometriske funktioner gør den trigonometriske ligning sand.
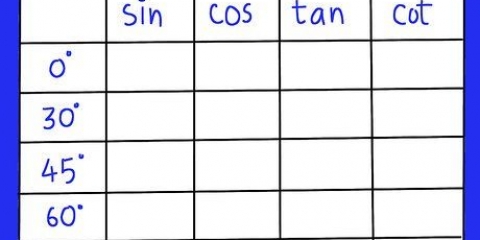
- Svar eller værdier af løsningskurverne er udtrykt i grader eller radianer. Eksempler:
x = Pi/3; x = 5Pi/6; x = 3Pi/2; x = 45 grader; x = 37,12 grader; x = 178,37 grader
- Bemærk: På enhedscirklen er de trigonometriske funktioner for enhver kurve lig med de trigonometriske funktioner i den tilsvarende vinkel. Enhedscirklen definerer alle trigonometriske funktioner af den variable kurve x. Det bruges også som bevis ved løsning af grundlæggende trigonometriske ligninger og uligheder.
- Eksempler på trigonometriske ligninger:
- sin x + sin 2x = 1/2; tan x + barneseng x = 1.732;
- cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1 .
- Enhedscirklen.
- Dette er en cirkel med Radius = 1, hvor O er oprindelsen. Enhedscirklen definerer 4 trigonometriske hovedfunktioner af den variable kurve x, som cirkler mod uret omkring den.
- Når kurven med værdien x varierer på enhedscirklen, gælder:
- Den vandrette akse OAx definerer den trigonometriske funktion f(x) = cos x.
- Den lodrette akse OBy definerer den trigonometriske funktion f(x) = sin x.
- Den lodrette akse AT definerer den trigonometriske funktion f(x) = tan x.
- Den vandrette akse BU definerer den trigonometriske funktion f(x) = cot x.
- Enhedscirklen bruges også til at løse grundlæggende trigonometriske ligninger og standard trigonometriske uligheder ved at overveje de forskellige positioner af kurven x på cirklen.
Trin

1. Forstå løsningsmetoden.
- For at løse en trigonometrisk ligning skal du konvertere den til en eller flere grundlæggende trigonometriske ligninger. Løsning af trigonometriske ligninger resulterer i sidste ende i løsning af 4 grundlæggende trigonometriske ligninger.

2. Vide, hvordan man løser grundlæggende trigonometriske ligninger.

3. Lær de transformationer, der bruges til at løse trigonometriske ligninger.

4. Find de kurver, hvis trigonometriske funktioner er kendte.

5. Tegn svarets bue på enhedscirklen.

6. Lær at løse trigonometriske ligninger.

7. Løs specielle trigonometriske ligninger.

8. Lær de periodiske egenskaber ved trigonometriske funktioner.
Artikler om emnet "Løsning af trigonometriske ligninger"
Оцените, пожалуйста статью
Populær