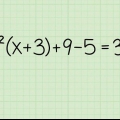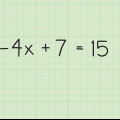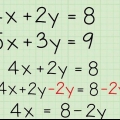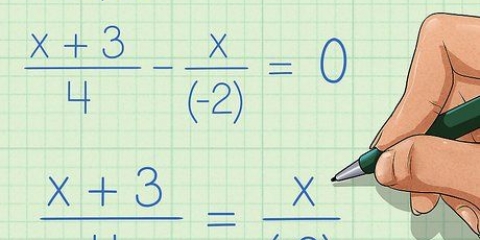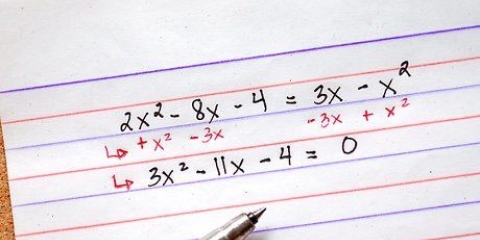Kryds multiplikation: 8 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Kryds multiplikation med én variabel
- Metode 2 af 2: Krydsmultiplikation med flere variable
Tips

Krydsmultiplikation er en måde at løse en ligning med en variabel som en del af to brøker, der er lig med hinanden. Variablen er et ukendt tal eller en ukendt mængde, og krydsmultiplikation gør denne brøkligning til en simpel ligning, så du kan løse den pågældende variabel. Krydsmultiplikation er især nyttig, når man prøver at løse et forhold. Sådan gør du det.

Trin

Metode 1 af 2: Kryds multiplikation med én variabel

Billede med titlen Cross Multiply Step 1

1. Gang tælleren for venstre brøk med nævneren i højre brøk. Lad os sige, at du arbejder på ligningen 2/x = 10/13. Gang nu 2 med 13. 2 x 13 = 26.

Billede med titlen Cross Multiply Step 2

2. Gang tælleren for den højre brøk med nævneren af den venstre brøk. Multiplicer med 10. x * 10 = 10x. Du kan krydse gange i denne retning først; det betyder ikke noget i sidste ende, så længe du gange begge tællere med de diagonale nævnere af den anden brøk.

Billede med titlen Cross Multiply Step 3

3. Gør de to produkter lige med hinanden. Gør 26 lig med 10x. 26 = 10x. Det er lige meget hvilket nummer du tager først; fordi de er ækvivalente, kan du flytte dem fra den ene side af ligningen til den anden uden konsekvenser; hvis du behandler hvert udtryk som en helhed.

Så hvis du prøver at løse for 2/x = 10/13 for x, får du 2 * 13 = x * 10 eller 26 = 10x.

Billede med titlen Cross Multiply Step 4

4. Løs for variablen. Nu hvor du har at gøre med 26 = 10x, kan du begynde at finde fællesnævneren ved at dividere både 26 og 10 med et tal, der har begge nævnere delelige med. Da de begge er lige tal, er det muligt at dividere dem med 2; 26/2 = 13 og 10/2 = 5. Nu står du tilbage med 13 = 5x som en ligning. For at isolere x skal du dividere begge sider af ligningen med 5. Så 13/5 = 5/5, eller 13/5 = x. Hvis du gerne vil have svaret som en decimalbrøk eller decimal, kan du dividere begge sider af ligningen med 10 for at få 26/10 = 10/10 eller 2.6 = x.

Metode 2 af 2: Krydsmultiplikation med flere variable

Billede med titlen Cross Multiply Step 5

1. Gang tælleren for venstre brøk med nævneren i højre brøk. Lad os sige, at du arbejder på følgende ligning: (x + 3)/2 = (x + 1)/4. Formere sig (x + 3) af 4 til 4(x +3) for at få. Dette er under udarbejdelse 4x + 12.

Billede med titlen Cross Multiply Step 6

2. Gang tælleren for den højre brøk med nævneren af den venstre brøk. Gentag denne procedure på den anden side. (x+1) x 2 = 2(x +1). Det bliver så 2(x +1) 2x + 2.

Billede med titlen Cross Multiply Step 7

3. Gør de to produkter ens med hinanden og kombiner lige vilkår. Nu har du 4x + 12 = 2x + 2. Kombiner x led og konstanterne på begge sider af ligningen.

Så kombiner 4x og 2x ved hjælp af 2x trække fra begge sider af ligningen. Udarbejdet giver dette følgende ligning 2x + 12 = 2.

Kombiner nu 12 og 2 ved hjælp af 12 trække fra begge sider af ligningen. Udarbejdet ser det sådan ud: 2x + 12-12 = 2-12.

Så ligningen bliver: 2x = -10.

Billede med titlen Cross Multiply Step 8

4. Løse. Alt du skal gøre nu er at dividere begge sider af ligningen med 2. 2x/2 = -10/2 = x = -5. Efter krydsmultiplikation vil du se, at x = -5. Du kan gå tilbage og kontrollere, at alt er korrekt ved at indtaste -5 for x for at sikre, at begge sider af ligningen er ens. Resultatet af denne kontrol er -1 = -1, og dette er sandt, fordi begge sider af ligningen er lige store. Ville kontrollen f.eks. 0 = -1 returnerer ligningen ikke korrekt, så noget gik galt.

Tips

Bemærk, at hvis du indtaster et andet tal (f.eks. 5) i samme ligning, får du følgende resultat: 2/5 = 10/13. Selv hvis du multiplicerer venstre side af ligningen med 5/5 igen, får du 10/25 = 10/13, hvilket klart er forkert. Dette sidste tilfælde viser tydeligt, at du lavede en fejl, når du multiplicerede på kryds og tværs.