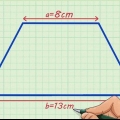
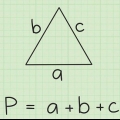For eksempel, hvis du har en trapez med en top på 2 cm, en bund på 3 cm og to sidelængder på 1 cm, vil din formel se sådan ud:


For eksempel:


Trapezoidens omkreds er derfor 7 cm. 

For eksempel, hvis du har en trapez med en højde på 6 cm, skal du tegne en linje fra hvert toppunkt til bunden. Bemærk 6 cm for hver linje. 
For eksempel, hvis toppen af trapezoidet er 6 cm, så er den midterste del af bunden også 6 cm. 

For eksempel, hvis du ved, at højden af trapezoidet er 6 cm og længden af siden (hypotenusen) er 9 cm, vil din ligning se sådan ud:


For eksempel: er ligningen  , så kvadrerer du 6 og 9, og trækker kvadratet af 6 fra kvadratet af 9:
, så kvadrerer du 6 og 9, og trækker kvadratet af 6 fra kvadratet af 9:




For eksempel:




Så tag det til efterretning som basis for den første trekant.
som basis for den første trekant. 
For eksempel, hvis den anden side af trapezoidet er 7 cm, beregnes som følger:





Så tag det til efterretning som bunden af den anden trekant.
som bunden af den anden trekant. 
For eksempel: 
Efter at have konverteret kvadratrødderne til decimaler, har du
Så den omtrentlige omkreds af din trapez er 38.314 cm.. 

For eksempel, hvis du har en trapez med en højde på 6 cm, skal du tegne en streg fra hvert toppunkt til bunden. Bemærk 6 cm ved hver linje. 
For eksempel, hvis toppen af trapezoidet er 6 cm, så er den midterste del af bunden også 6 cm. 
Med dette forhold kan du finde længden af hypotenusen i trekanten, som også er den første side af trapezoidet. Hypotenusen er siden modsat 90 graders vinkel i en retvinklet trekant. 
Antag, at den givne indvendige vinkel er 35 grader, og højden af trekanten er 6 cm, så vil din formel se sådan ud:


For eksempel vil du ved at bruge en lommeregner opdage, at sinus for en 35 graders vinkel er 0,5738 (afrundet). Så din formel er nu:


For eksempel:




Således er længden af hypotenusen og den første manglende side af trapezet omkring 10,4566 cm. 
For eksempel, hvis den givne indvendige vinkel er 45 grader, beregn:





Så længden af hypotenusen og den anden manglende side af trapezoidet er omkring 8,4854 cm. 

For eksempel, hvis den første retvinklede trekant har en hypotenusa på 10,4566 og en højde på 6, er din formel:


For eksempel:






Så bunden af trekanten og den første manglende del af bunden af trapezet er omkring 8,5639 cm. 
For eksempel, hvis den anden retvinklede trekant har en hypotenusa på 8,4854 og en højde på 6, vil du beregne som følger:






Så bunden af den anden trekant og den anden manglende del af bunden af trapezoiden er lig med 6 cm. 
For eksempel: 
Så den omtrentlige omkreds af trapezoidet er 45,5059 cm.
Beregning af omkredsen af en trapez
Indhold
Et trapez er defineret som en firkant med to parallelle sider. Som med enhver polygon skal du lægge alle fire sider sammen for at finde omkredsen af et trapez (eller trapez). Ofte vil du dog savne sidelængder, men du har andre data, såsom højden af trapez eller vinkelmålingerne. Ved hjælp af disse data kan du finde de ukendte længder af siderne ved hjælp af reglerne for geometri og trigonometri.
Trin
Metode 1 af 3: Hvis du kender længden af begge sider og basen

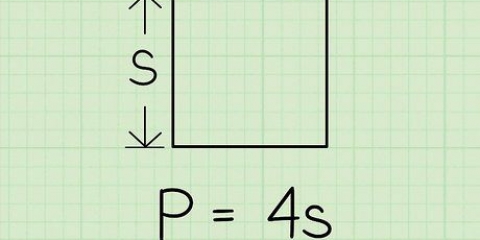
1. Indstil formlen for omkredsen af en trapez. Formlen er  , hvorved
, hvorved  er lig med omkredsen af trapezet og variablen
er lig med omkredsen af trapezet og variablen  er lig med længden af toppen af trapez,
er lig med længden af toppen af trapez,  er lig med længden af bunden,
er lig med længden af bunden,  er lig med længden af venstre side og
er lig med længden af venstre side og  er lig med længden af højre side.
er lig med længden af højre side.
 , hvorved
, hvorved  er lig med omkredsen af trapezet og variablen
er lig med omkredsen af trapezet og variablen  er lig med længden af toppen af trapez,
er lig med længden af toppen af trapez,  er lig med længden af bunden,
er lig med længden af bunden,  er lig med længden af venstre side og
er lig med længden af venstre side og  er lig med længden af højre side.
er lig med længden af højre side.
2. Brug sidelængderne i formlen. Hvis du ikke kender længden af alle fire sider af trapezoidet, kan du ikke bruge denne formel.


3. Læg sidelængderne sammen. Dette vil give dig omkredsen af din trapez.


Trapezoidens omkreds er derfor 7 cm.
Metode 2 af 3: Hvis du kender højden, begge sidelængder og toplængden

1. Opdel trapezet i et rektangel og to retvinklede trekanter. For at gøre dette skal du tegne højden fra begge øverste hjørner.
- Hvis du ikke kan danne de to retvinklede trekanter, fordi den ene side af trapezoidet er vinkelret på basen, skal du sørge for, at denne side har samme længde som højden, og opdele trapezet i et rektangel og en retvinklet trekant.

2. Angiv længden af hver konturlinje. Da disse er de modsatte sider af et rektangel, vil de have samme længde.

3. Bemærk længden af den midterste del af bunden. (Dette er bunden af rektanglet.) Længden vil være lig med længden af toppen (toppen af rektanglet), fordi de modsatte sider af et rektangel har samme længde. Hvis du ikke kender længden af toppen, kan du ikke bruge denne metode.

4. Opstil Pythagoras sætning for den første retvinklede trekant. Formlen er  , hvorved
, hvorved  er længden af hypotenusen i den retvinklede trekant (siden modsat den rette vinkel),
er længden af hypotenusen i den retvinklede trekant (siden modsat den rette vinkel),  er højden af den retvinklede trekant og
er højden af den retvinklede trekant og  er længden af trekantens base.
er længden af trekantens base.
 , hvorved
, hvorved  er længden af hypotenusen i den retvinklede trekant (siden modsat den rette vinkel),
er længden af hypotenusen i den retvinklede trekant (siden modsat den rette vinkel),  er højden af den retvinklede trekant og
er højden af den retvinklede trekant og  er længden af trekantens base.
er længden af trekantens base.
5. Brug de kendte værdier af den første trekant i formlen. Sørg for at indtaste sidelængden af trapezformen for  . Indtast højden af trapez for
. Indtast højden af trapez for  .
.
 . Indtast højden af trapez for
. Indtast højden af trapez for  .
.

6. Kvaddre de kendte værdier i ligningen. Træk derefter de kvadrerede værdier fra hinanden for at få  at isolere.
at isolere.
 at isolere.
at isolere. , så kvadrerer du 6 og 9, og trækker kvadratet af 6 fra kvadratet af 9:
, så kvadrerer du 6 og 9, og trækker kvadratet af 6 fra kvadratet af 9:



7. Tag kvadratroden for at få værdien af b  at finde. (For fuldstændige instruktioner om forenkling af kvadratrødder, læs denne artikel om emnet). Resultatet vil give dig værdien af den manglende base i din første retvinklede trekant. Skriv denne længde i bunden af din trekant.
at finde. (For fuldstændige instruktioner om forenkling af kvadratrødder, læs denne artikel om emnet). Resultatet vil give dig værdien af den manglende base i din første retvinklede trekant. Skriv denne længde i bunden af din trekant.
 at finde. (For fuldstændige instruktioner om forenkling af kvadratrødder, læs denne artikel om emnet). Resultatet vil give dig værdien af den manglende base i din første retvinklede trekant. Skriv denne længde i bunden af din trekant.
at finde. (For fuldstændige instruktioner om forenkling af kvadratrødder, læs denne artikel om emnet). Resultatet vil give dig værdien af den manglende base i din første retvinklede trekant. Skriv denne længde i bunden af din trekant.



Så tag det til efterretning
 som basis for den første trekant.
som basis for den første trekant.
8. Find den manglende længde af den anden retvinklede trekant. For at gøre dette skal du opsætte Pythagoras sætning for den anden trekant og følge trinene for at finde længden af den manglende side. Hvis du arbejder med en ligebenet trapez (den, hvor de to ikke-parallelle sider har samme længde), så er de to rette trekanter kongruente, så værdien af den første trekant er lig med værdien af den anden trekant.





Så tag det til efterretning
 som bunden af den anden trekant.
som bunden af den anden trekant.
9. Læg alle sidelængderne af trapezet sammen. Omkredsen af enhver polygon er summen af alle sider:  . For bunden skal du tilføje den nederste side af rektanglet plus baserne af de to trekanter. Du vil sandsynligvis have kvadratrødder i dit svar. For fuldstændige instruktioner om at tilføje kvadratrødder, læs artiklen om dette emne. Du kan også bruge en lommeregner til at konvertere kvadratrødderne til decimaler.
. For bunden skal du tilføje den nederste side af rektanglet plus baserne af de to trekanter. Du vil sandsynligvis have kvadratrødder i dit svar. For fuldstændige instruktioner om at tilføje kvadratrødder, læs artiklen om dette emne. Du kan også bruge en lommeregner til at konvertere kvadratrødderne til decimaler.
 . For bunden skal du tilføje den nederste side af rektanglet plus baserne af de to trekanter. Du vil sandsynligvis have kvadratrødder i dit svar. For fuldstændige instruktioner om at tilføje kvadratrødder, læs artiklen om dette emne. Du kan også bruge en lommeregner til at konvertere kvadratrødderne til decimaler.
. For bunden skal du tilføje den nederste side af rektanglet plus baserne af de to trekanter. Du vil sandsynligvis have kvadratrødder i dit svar. For fuldstændige instruktioner om at tilføje kvadratrødder, læs artiklen om dette emne. Du kan også bruge en lommeregner til at konvertere kvadratrødderne til decimaler.
Efter at have konverteret kvadratrødderne til decimaler, har du

Så den omtrentlige omkreds af din trapez er 38.314 cm..
Metode 3 af 3: Hvis du kender højden, længden af de øverste og de nederste indre hjørner

1. Opdel trapezet i et rektangel og to retvinklede trekanter. Til dette angives højden fra begge øverste hjørner.
- Hvis du ikke kan danne to retvinklede trekanter, fordi den ene side af trapezet er vinkelret på basen, skal du sørge for, at denne side har samme størrelse som højden, og dele trapezet i et rektangel og en retvinklet trekant.

2. Mærk hver kontur. Da disse er modsatte sider af et rektangel, vil de have samme længde.

3. Bemærk længden af den midterste del af bunden. (Dette er bunden af rektanglet.) Denne længde vil være lig med længden af toppen, fordi de modsatte sider af et rektangel har samme længde.

4. Indstil sinusformlen for den første retvinklede trekant. Formlen er  , hvorved
, hvorved  det indvendige hjørne er,
det indvendige hjørne er,  højden af trekanten og
højden af trekanten og  er længden af hypotenusen.
er længden af hypotenusen.
 , hvorved
, hvorved  det indvendige hjørne er,
det indvendige hjørne er,  højden af trekanten og
højden af trekanten og  er længden af hypotenusen.
er længden af hypotenusen.
5. Brug de kendte værdier i sinusforholdet. Sørg for at bruge højden af trekanten som længden af den modsatte side i formlen. du løser dette for H.


6. Bestem vinklens sinus. Gør dette ved at bruge SIN-knappen på en videnskabelig lommeregner. Brug denne værdi i formlen.


7. Løs dette for H. For at gøre dette skal du gange hver side med H og derefter dividere hver side med sinusvinklen. Eller divider højden af trekanten med sinusvinklen.




Således er længden af hypotenusen og den første manglende side af trapezet omkring 10,4566 cm.

8. Find længden af hypotenusen i den anden retvinklede trekant. Indstil sinusformlen ( ) for den anden givne indvendige vinkel. Dette vil give dig længden af hypotenusen, som også er den første side af trapezoidet.
) for den anden givne indvendige vinkel. Dette vil give dig længden af hypotenusen, som også er den første side af trapezoidet.
 ) for den anden givne indvendige vinkel. Dette vil give dig længden af hypotenusen, som også er den første side af trapezoidet.
) for den anden givne indvendige vinkel. Dette vil give dig længden af hypotenusen, som også er den første side af trapezoidet.




Så længden af hypotenusen og den anden manglende side af trapezoidet er omkring 8,4854 cm.

9. Opstil Pythagoras sætning for den første retvinklede trekant. Pythagoras sætning er høj  , hvor længden af hypotenusen er lig med
, hvor længden af hypotenusen er lig med  , og højden af trekanten
, og højden af trekanten  .
.
 , hvor længden af hypotenusen er lig med
, hvor længden af hypotenusen er lig med  , og højden af trekanten
, og højden af trekanten  .
.
10. Brug de kendte værdier i Pythagoras sætning for den første retvinklede trekant. Sørg for at indtaste den korrekte værdi for hypotenusen  og højden
og højden  .
.
 og højden
og højden  .
.

11. Løs dette for b  . Dette vil give dig længden af bunden af den første retvinklede trekant og den første manglende del af bunden af trapezoidet.
. Dette vil give dig længden af bunden af den første retvinklede trekant og den første manglende del af bunden af trapezoidet.
 . Dette vil give dig længden af bunden af den første retvinklede trekant og den første manglende del af bunden af trapezoidet.
. Dette vil give dig længden af bunden af den første retvinklede trekant og den første manglende del af bunden af trapezoidet.





Så bunden af trekanten og den første manglende del af bunden af trapezet er omkring 8,5639 cm.

12. Find længden af den manglende base i den anden retvinklede trekant. Brug Pythagoras sætning ( ). Brug længden af hypotenusen til
). Brug længden af hypotenusen til  og højden for
og højden for  . Løs dette for
. Løs dette for  og du får længden af den anden manglende del af bunden af trapez.
og du får længden af den anden manglende del af bunden af trapez.
 ). Brug længden af hypotenusen til
). Brug længden af hypotenusen til  og højden for
og højden for  . Løs dette for
. Løs dette for  og du får længden af den anden manglende del af bunden af trapez.
og du får længden af den anden manglende del af bunden af trapez.





Så bunden af den anden trekant og den anden manglende del af bunden af trapezoiden er lig med 6 cm.

13. Læg alle sider af trapezet sammen. Omkredsen af enhver polygon er summen af alle sider:  . For bunden skal du tilføje bunden af rektanglet til bunden af de to trekanter.
. For bunden skal du tilføje bunden af rektanglet til bunden af de to trekanter.
 . For bunden skal du tilføje bunden af rektanglet til bunden af de to trekanter.
. For bunden skal du tilføje bunden af rektanglet til bunden af de to trekanter.
Så den omtrentlige omkreds af trapezoidet er 45,5059 cm.
Tips
- Brug lovene for specielle trekanter til at finde de manglende længder af specielle trekanter uden at bruge sinusformlen eller Pythagoras sætning. Lovene gælder for en 30-60-90 trekant eller en 90-45-45 trekant.
- Brug en videnskabelig lommeregner til at bestemme sinus af en vinkel ved at indtaste vinklen og derefter trykke på `SIN`-knappen. Du kan også bruge en trigonometritabel.
Fornødenheder
- Lommeregner
- Blyant
- Papir
Artikler om emnet "Beregning af omkredsen af en trapez"
Оцените, пожалуйста статью
Lignende
Populær