Beregning af apotem af en sekskant: 15 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Brug af Pythagoras sætning (radiuslængde er givet)
- Metode 2 af 2: Brug af trigonometri (og en given radius)
Tips

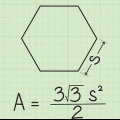
En sekskant er en polygon med seks vinkler og sider. Når en sekskant er regulær, har den seks lige store sider og en apotem. Et apotem er et linjestykke fra midten af en polygon til midten af hver side. Normalt skal længden af apotem angives for at beregne arealet af en sekskant. Så længe du kender længden af siden af sekskanten, kan du beregne længden af apotemet.

Trin

Metode 1 af 2: Brug af Pythagoras sætning (radiuslængde er givet)

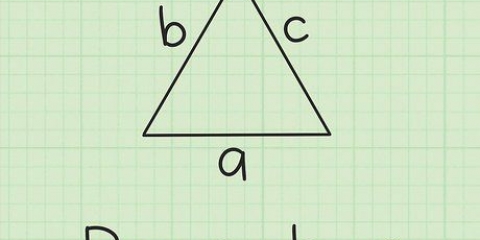
1. Opdel sekskanten i seks kongruente ligesidede trekanter. For at gøre dette skal du tegne en linje fra hvert toppunkt eller punkt til det modsatte toppunkt.

Billede med titlen Beregn apotem af en sekskant Trin 2

2. Vælg en trekant og skriv længden af basen ned. Det er lig med længden af siden af sekskanten.

For eksempel har du en sekskant med en længde på 8 cm til siden. Grundlaget for enhver ligesidet trekant er derfor 8 cm.

Billede med titlen Beregn apotem af en sekskant Trin 3

3. Lav to rette trekanter. Det gør du ved at tegne en linje fra det øverste toppunkt af den ligesidede trekant vinkelret på basen. Denne linje halverer trekantens basis (så det er sekskantens apotem). Mærk længden af bunden af en af de rette trekanter.

For eksempel, hvis bunden af den ligesidede trekant er 8 cm, så er bunden af enhver retvinklet trekant -- når du deler trekanten i to rette trekanter -- nu lig med 4 cm.

Billede med titlen Beregn apotem af en sekskant Trin 4

4. Brug Pythagoras sætning. Formlen er

-en 2 + b^{2} = c^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , hvorved

c

$c$ er lig med længden af hypotenusen (siden modsat den rette vinkel), og

-en

$-en$ og

b

$b$ være lig med længderne af trekantens to andre sider.

For eksempel, hvis den retvinklede trekant har en hypotenus på

2

$2$ den ene side af

1

$1$ og en anden side af ca

1, 732

$1.732$ (

\sqrt{3}

${sqrt{3}}$ ), så siger Pythagoras sætning det

12 + {\sqrt{3}}^{2} = 2^{2}

$1^{{2}}+{sqrt{3}}^{{2}}=2^{{2}}$ , hvilket er korrekt, når du regner dette ud:

1 + 3 = 4

$1+3=4$ .

Billede med titlen Beregn apotem af en sekskant Trin 5

5. Erstat længden af bunden af den retvinklede trekant i formlen. Stedfortræder for

b

$b$ .

For eksempel, hvis længden af basen er 4, vil din formel se sådan ud:

-en 2 + 4^{2} = c^{2}

$a^{{2}}+4^{{2}}=c^{{2}}$ .

Billede med titlen Beregn apotem af en sekskant Trin 6

6. Erstat længden af hypotenusen i formlen. Du kender længden af hypotenusen, fordi du kender længden af sekskanten. Længden af siden af en regulær sekskant er lig med radius af sekskanten. Radius er en linje, der forbinder midten af en polygon med en af dens hjørner. Du vil se, at hypotenusen af den retvinklede trekant også er radius af sekskanten, så længden af siden af sekskanten er lig med længden af hypotenusen.

For eksempel, hvis længden af siden af sekskanten er 8 cm, så er længden af hypotenusen i den retvinklede trekant også 8 cm. Så din formel vil nu se sådan ud:

-en 2 + 4^{2} = 8^{2}

$a^{{2}}+4^{{2}}=8^{{2}}$ .

Billede med titlen Beregn apotem af en sekskant Trin 7

7. Kvadret de kendte værdier af formlen. Husk, at at kvadrere et tal er det samme som at gange det tal med sig selv.

For eksempel, efter at have kvadreret de kendte værdier, vil din formel se sådan ud:

-en 2 + 16 = 64

$a^{{2}}+16=64$ .

Billede med titlen Beregn apotem af en sekskant Trin 8

8. Isoler den ukendte variabel. Det gør du ved at trække den kvadratiske værdi fra

b

$b$ fra begge sider af ligningen.

For eksempel:

-en 2 + 16 - 16 = 64 - 16

$a^{{2}}+16-16=64-16$

-en 2 = 48

$a^{{2}}=48$

Billede med titlen Beregn apotem af en sekskant Trin 9

9. Løs for -en{displaystyle a} $-en$ . Det gør du ved at bestemme kvadratroden af hver side af ligningen. Dette vil give dig længden af den manglende side af trekanten, som er lig med længden af sekskantens apotem.

For eksempel ved hjælp af en lommeregner du beregner

\sqrt{48} = 6, 93

${sqrt{48}}=6,93$ . Så den manglende længde af den retvinklede trekant, og dermed længden af sekskantens apotem, er lig med 6,93 cm.

Metode 2 af 2: Brug af trigonometri (og en given radius)

Billede med titlen Beregn apotem af en sekskant Trin 10

1. Skriv formlen for at finde apotemet for en regulær polygon. Formlen er

apotem = s 2 \tan (\frac{180}{n})

${text{apothema}}={frac{s}{2tan({frac{180}{n}})}}$ , hvorved

s

$s$ er lig med længden af siden af polygonen og

n

$n$ er lig med antallet af sider af polygonen.

Billede med titlen Beregn apotem af en sekskant Trin 11

2. Erstat længden af siden i formlen. Glem ikke at erstatte variablen

s

$s$ .

For eksempel, for en sekskant med en sidelængde på 8 cm, vil formlen se sådan ud:

8 2 \tan (\frac{180}{n})

${frac{8}{2tan({frac{180}{n}})}}$ .

Billede med titlen Beregn apotem af en sekskant Trin 12

3. Indtast antallet af sider i formlen. En sekskant har 6 sider. Glem ikke at erstatte variablen

n

$n$ .

For eksempel:

8 2 \tan (\frac{180}{6})

${frac{8}{2tan({frac{180}{6}})}}$ .

Billede med titlen Beregn apotem af en sekskant Trin 13

4. Afrund regnestykket i parentes. Dette giver dig det antal grader, der skal til for at beregne tangenten.

For eksempel,

\frac{180}{6} = 30

${frac{180}{6}}=30$ , hvormed formlen nu ser sådan ud:

8 2 \tan (30)

${frac{8}{2tan(30)}}$ .

Billede med titlen Calculate the Apothem of a Hexagon Trin 14

5. Bestem tangenten. Brug en lommeregner eller trigonometrisk tabel til dette.

For eksempel er tangenten til 30 omkring 0,577, så formlen ville se sådan ud:

8 2 (0, 577)

${frac{8}{2(0.577)}}$ .

Billede med titlen Beregn apotem af en sekskant Trin 15

6. Multiplicer tangenten med 2 og divider derefter længden af den ene side med dette tal. Med dette har du beregnet længden af apotemet for din sekskant.

For eksempel:

apotem = 8 2 (0, 577)

${text{apothema}}={frac{8}{2(0.577)}}$

apotem = 8 1, 154

${text{apothema}}={frac{8}{1.154}}$

apotem = 6, 93

${text{apothema}}=6,93$
Så apotemet for en regulær sekskant med sider på 8 cm er omkring 6,93 cm.

Tips

Udtrykket "apothema" kan referere til det faktiske linjestykke eller til længden af det linjestykke.
Husk, at denne metode kun virker med almindelige sekskanter. Uregelmæssige sekskanter har ingen apotem.