Beregning af volumen af en terning

Indhold

Trin

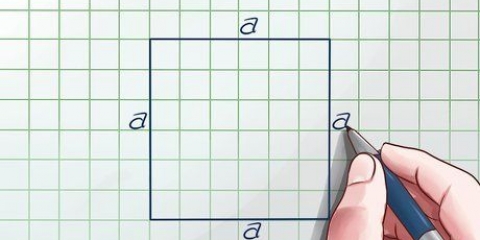
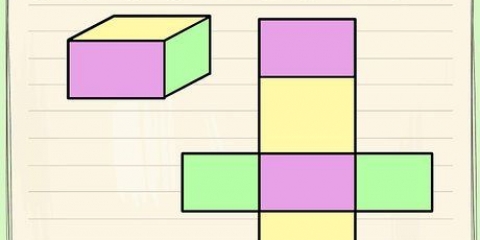
En terning er en tredimensionel figur, hvis længde, bredde og højde er ens. En terning har seks kvadratiske flader, hvis sider er lige lange og vinkelrette på hinanden. At beregne rumfanget af en terning er meget simpelt - normalt skal du bare gange følgende: længde × bredde × højde. Fordi kanterne på en terning alle har samme længde, kan du også se rumfanget af en terning som følger: l, hvorved l er længden af en af terningens kanter. Gå til trin 1 for en detaljeret forklaring.

Trin

Metode 1 af 3: Hævning af kanten af terningen til terningen

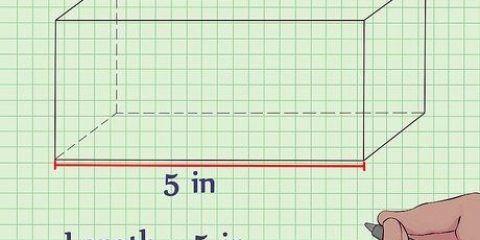
1. Find længden af en af terningens kanter. Ofte vil du se en sum, hvor længden af et af ribbenene allerede er angivet. Når du har disse oplysninger, har du alt hvad du behøver for at bestemme terningens volumen. Brug en lineal eller et målebånd, hvis du ikke løser et matematisk problem, men bare vil vide volumen af et eksisterende terningformet objekt.

For bedre at forstå processen med at bestemme rumfanget af en terning, lad os starte med en eksempelsum, mens vi går gennem trinene i dette afsnit. Antag, at kanten af terningen 2 cm lang er. Vi vil bruge denne information i næste trin til at bestemme terningens volumen.

Billede med titlen Beregn volumen af en terning Trin 2

2. Hæv længden af ribben til tredje potens. Når du har længden af et af ribbenene, så hæv dette tal til tredje potens. Med andre ord, gange tallet to gange med sig selv. hvis l er længden af ribben, så ganger du l × l × l (eller i enklere form l). Resultatet er terningens rumfang.

Denne proces er grundlæggende det samme som at beregne arealet af basen først og derefter gange dette område med terningens højde (eller med andre ord længde × bredde × højde), fordi arealet af basen bestemmes ved at gange længden med bredden. Da længden, bredden og højden af en terning er ens, kan vi forenkle processen ved at hæve en af disse værdier til tredje potens.

Lad os fortsætte med vores eksempel. Længden af kanten var 2 cm, så rumfanget af terningen er 2 x 2 x 2 (eller 2)= 8.

Billede med titlen Beregn volumen af en terning Trin 3

3. Angiv dit svar i kubikenheder. Volumen er målet for et tredimensionelt rum, så løsningen skal skrives i kubikenheder. På en test kan det koste dig point, hvis du ikke angiver svaret korrekt i kubikenheder, så glem det ikke!

I vores eksempel var ribbens længde angivet i centimeter, så svaret skal angives i kubikcentimeter. Så svaret er 8 cm.

Metode 2 af 3: Bestemmelse af volumen efter overfladeareal

Billede med titlen Beregn volumen af en terning Trin 4

1. Find arealet af ansigterne på din terning. Det nemmeste måde at bestemme volumen er ved at hæve ribben til terningen, men det er ikke nogen vej. Længden af kanten af en terning eller arealet af en af dens flader kan afledes af flere andre egenskaber ved terningen, hvilket betyder, at hvis du starter med denne information, kan du bestemme terningens volumen på en afledt måde. For eksempel, hvis du kun kender det samlede areal af alle siderne af terningen, kan du finde volumen ved at dividere dette område med seks og derefter tage kvadratroden af det tal for at finde længden af kanten. Fra det tidspunkt kan du hæve til tredje potens igen. I dette afsnit gennemgår vi denne proces trin for trin.

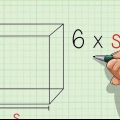
Arealet af en terning er givet af formlen 6l, hvorved l er længden af en af terningens kanter. Denne formel er faktisk det samme som at bestemme det todimensionelle areal af en af siderne af terningen og derefter tilføje de seks (lige) områder. Vi vil bruge denne formel til at bestemme terningens rumfang ud fra terningens område.
Antag, at vi har en terning, som vi kender området af 50 cm er, men vi ved ikke, hvad længden af ribbenene er. I de næste trin vil vi bruge denne information til at finde terningens volumen.

Billede med titlen Beregn volumen af en terning Trin 5

2. Del terningens areal med seks. Da terningen har seks flader med samme areal, kan vi bestemme arealet af et ansigt ved at dividere terningens areal med seks. Arealet af et plan er det samme som multiplikationen af to kanter (l × b, b × h eller h × l).

Så i vores eksempel dividerer vi halvtreds med seks: 50/6 = 8,33 cm. Husk, at enhederne for todimensionelle svar skrives i kvadrat (cm, m og så videre).

Billede med titlen Beregn volumen af en terning Trin 6

3. Find kvadratroden af denne værdi. Da arealet af en af overfladerne af en terning er lig med l (l × l), kan vi nu tage kvadratroden af den fundne værdi for at bestemme længden af en af ribberne. Når du ved dette, har du nok information til at beregne terningens rumfang som normalt.

I vores eksempel er √8,33 = 2,89 cm.

Billede med titlen Beregn volumen af en terning Trin 7

4. Hæv dette tal til tredje potens for at finde terningens volumen. Nu hvor du har bestemt en værdi for længden af ribbenene, kan du hæve dette tal til terningen for at bestemme volumen som beskrevet i første afsnit af denne artikel.

Så i vores eksempel: 2,89 × 2,89 × 2,89 = 24,14 cm. Glem ikke at skrive svaret i kubikenheder.

Metode 3 af 3: Bestemmelse af volumen ved hjælp af diagonaler

Billede med titlen Beregn volumen af en terning Trin 8

1. Divider diagonalen af en af terningens flader med √2 for at finde længden af terningens kanter. Diagonalen af et kvadrat er √2 × længden af en af dets kanter. Med andre ord, hvis du kun kender værdien af en af diagonalerne på en flade af terningen, kan du beregne længden af terningens kanter ved at dividere denne værdi med √2. Fra det tidspunkt kan du hæve til tredje potens igen og bestemme lydstyrken som beskrevet ovenfor.

Antag, at en af terningens flader har en diagonal på7 meter lang. Så kan vi beregne længden af et af ribbenene ved at dividere 7 med √2. 7/√2 = 4,96 meter. Nu hvor vi kender længden af terningens kanter, kan vi beregne rumfanget af terningen ved at hæve 4,96 til terningen: 4,96 = 122,36 meter.
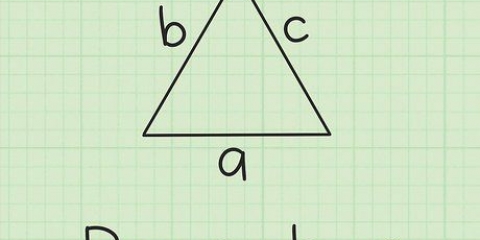
Vær opmærksom: d = 2l, rigtigt d er længden af diagonalen af en af terningens flader og l er længden af en af terningens kanter. Dette kan udledes af Pythagoras sætning, hvor kvadratet af hypotenusen i en ligesidet trekant er lig med summen af kvadratet af de to andre sider. Da diagonalen af en flade af en terning danner en ligesidet trekant med to af kanterne på den flade, kan vi sige følgende: d = l + l = 2l.

Billede med titlen Beregn volumen af en terning Trin 9

2. Find kvadratet af diagonalen mellem to modstående hjørner af terningen, divider med tre og tag kvadratroden for at finde længden af en af kanterne. Hvis længden af den tredimensionelle linje mellem to modstående hjørner af terningen er den eneste givne, kan du stadig bestemme terningens rumfang. d danner en af siderne i en ligesidet trekant, hvis hypotenuse er linjen mellem to modstående hjørner af terningen, så vi kan sige: d = 3l, hvor D er den tredimensionelle linje mellem to modstående hjørner af terningen.

Dette kan også udledes af Pythagoras sætning. d, d og l danner en ligesidet trekant med D som hypotenusen, så d = d + l. Tidligere havde vi allerede bestemt: d = 2l, så vi kan også sige følgende: d = 2l + l = 3l.

Antag, at vi ved, at længden af diagonalen, der løber fra det ene hjørne i bunden af kuben til det modsatte hjørne i den øverste flade af kuben, er 10 meter. Så hvis vi vil beregne volumen, indtaster vi 10 i ovenstående formel for d.

d = 3l.

10 = 3l.

100 = 3l

33.33 = l

5.77 m = l. Fra dette punkt kan vi beregne volumenet ved at hæve længden af ribben til terningen.

5.77 = 192.45 m