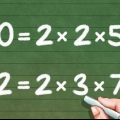Find den største fælles divisor: 6 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Sammenlign fællesnævnere
- Metode 2 af 2: Brug af primtal
Tips

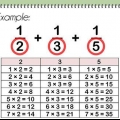
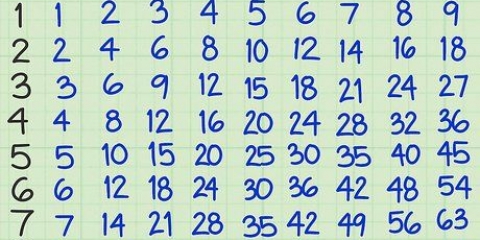
Det er nemt at bestemme den største fælles divisor (GGD) for et sæt tal, men der er flere trin, du skal følge for at komme dertil. For at finde den største fælles divisor af to tal, skal du faktorisere begge tal ved hjælp af din viden om multiplikationstabeller, og derefter finde det største tal i begge sæt af faktorer.

Trin

Metode 1 af 2: Sammenlign fællesnævnere

1. Bestem tallets faktorer. Du behøver ikke prime faktorer for at finde den største fælles divisor. Start med at finde alle faktorerne for de tal, du sammenligner.

Billede med titlen Find den største fælles faktor Trin 2

2. Sammenlign sættene af faktorer, indtil du finder det største tal i begge sæt.

Metode 2 af 2: Brug af primtal

Billede med titlen Find den største fælles faktor Trin 3

1. Faktorer hvert tal fuldt ud i primtal. Et primtal er et tal større end 1, som kun er deleligt med 1 og sig selv. Eksempler på primtal er 5, 17, 97 og 331, for blot at nævne nogle få. For eksempel:

42 = 2 x 3 x 7
35 = 5 x 7
Faktoriseringen af et primtal til primfaktorer er bare sig selv. 5 = 5, 23 = 23 osv.

Billede med titlen Find den største fælles faktor Trin 4

2. Bestem de fælles primfaktorer. Vælg mellem alle primtal mellem sættene, der er ens. Der kan være flere almindelige primtalsdelere.

Billede med titlen Find den største fælles faktor Trin 5

3. Beregn. Hvis der kun er én fælles primfaktor, er det din fællesnævner. Hvis der er flere fælles primfaktorer, gange så alle de fælles primfaktorer sammen for at få den største fælles divisor.

4. For at demonstrere denne metode studerer vi følgende eksempel. Find den største fælles divisor fra 24 og 84.

Faktorisering i primfaktorer: 24 = 2 x 2 x 2 x 3 og 84 = 2 x 2 x 3 x 7

Bestem fælles primfaktorer: 24 = 2 x 2 x 2 x 3 og 84 = 2 x 2 x 3 x 7

Multiplikation af almindelige primfaktorer: 2 x 2 x 3 = 12

Tips

Et primtal er et tal, der kun kan divideres med 1 og sig selv.
Vidste du, at matematikeren Euklid fra det tredje århundrede fvt skabte en algoritme til at finde den største fælles divisor af to naturlige tal eller to polynomier?