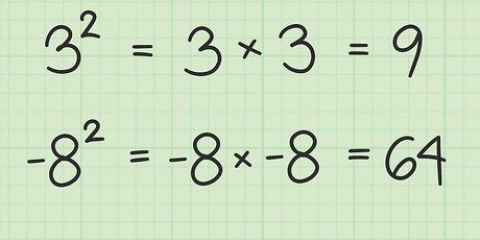Faktorering af et tal: 11 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Faktorisering af heltal
- Metode 2 af 2: Big Number Factoring-strategi
Tips
Advarsler
Fornødenheder

Faktorerne for et givet produktnummer er de tal, der, når de ganges sammen, giver det pågældende produkt. En anden måde at tænke dette på er, at hvert tal er et produkt af flere faktorer. At lære at faktorisere er en vigtig matematisk færdighed, der ikke kun bruges i aritmetik, men også i algebra, analyse og andre matematiske felter. Læs videre for at lære mere om faktorisering!

Trin

Metode 1 af 2: Faktorisering af heltal

1. Skriv nummeret ned. Du kan faktorisere et hvilket som helst tal, men for nemheds skyld starter vi med et heltal. Hele tal er positive eller negative tal uden brøker eller decimaler.

tag nummeret 12. Skriv dette på et stykke papir.

2. Find yderligere to tal, der ganges sammen danner det første tal som et produkt. Ethvert heltal kan skrives som produktet af to andre heltal. Selv primtal kan skrives som produktet af 1 og selve primtallet. At tænke i faktorer kræver en anden måde at ræsonnere på. Du spørger faktisk dig selv, "hvilken multiplikation er lig med dette tal?"

I vores eksempel har 12 flere faktorer - 12 × 1, 6 × 2 og 3 × 4 - alle er lig med 12. Så det kan vi sige 1, 2, 3, 4, 6 og 12 er alle faktorer på 12. Til vores formål er det tilstrækkeligt at fortsætte med faktor 6 og 2.

Lige tal er særligt nemme at faktorisere, fordi disse tal altid har en faktor på 2. 4 = 2 × 2, 26 = 13 × 2 osv.

3. Afgør, om de valgte faktorer selv kan opløses igen. Mange tal - især de større - kan faktoriseres flere gange. Afhængigt af situationen kan du måske eller ikke have gavn af dette.

For eksempel har vi indregnet 12 til 2 × 6. Bemærk, at 6 igen kan indregnes i faktorerne 3 × 2 = 6. Så vi kan sige, at 12 = 2×(3×2).

4. Stop factoring, når du støder på en prime faktor. Primtal er tal, der er delelige med 1 og sig selv. For eksempel er 1, 2, 3, 5, 7, 11, 13 og 17 alle primtal. Hvis du har faktoriseret et tal til det punkt, hvor der kun er primtal tilbage, nytter det ikke at fortsætte, fordi de eneste faktorer tilbage er 1 og selve primtallet.

I vores eksempel opløste vi 12 og forenklede det til 2 × (2 × 3). 2, 2 og 3 er alle primtal. Hvis vi skulle gå endnu længere, ville vi skulle faktorisere (2 × 1) × ((2 × 1)(3 × 1)), hvilket ikke længere er til nogen nytte for dig..

5. Løs negative tal på samme måde. Negative tal kan faktoriseres på næsten samme måde som positive tal. Den store forskel er, at faktorerne ganget sammen skal få et negativt tal som produktet, så et ulige antal af faktorerne skal være negativt.

Lad os faktor 60 som et eksempel. Se mere nedenfor:

-60 = -10 × 6

-60 = (-5 × 2) × 6

-60 = (-5 × 2) × (3 × 2)

-60 = -5×2×3×2. Bemærk, at have et ulige antal negative tal ved siden af 1`et returnerer det samme produkt. For eksempel, -5 × 2 × -3 × -2 er også lig med 60.

Metode 2 af 2: Big Number Factoring-strategi

1. Skriv dit nummer øverst i en tabel med 2 kolonner. Selvom det normalt er meget nemt at faktorisere mindre tal, kan større tal nogle gange være ret skræmmende. De fleste af os ville have svært ved at tage højde for et 4- eller 5-cifret tal uden andet end din hjerne. Det bliver heldigvis meget nemmere ved hjælp af et bord.

Vælg et 4-cifret tal til faktor - 6552.

2. Divider dit tal med den mindst mulige primfaktor, undtagen 1. Skriv primtallet i venstre kolonne og svaret i næste kolonne. Som beskrevet ovenfor er lige tal det nemmeste at faktorisere, fordi det mindste primtal (undtagen 1) altid er lig med 2. Ulige tal har på den anden side forskellige mindste primfaktorer.

I vores eksempel ved vi, at 2 er den mindste primfaktor, fordi 6552 er et lige tal. 6552 2 = 3276. I venstre kolonne skriver vi 2 og til højre 3276.

3. Fortsæt faktoriseringen på denne måde. Faktorer nu tallet i højre kolonne og find den mindste primfaktor af dette tal. Skriv det under den tidligere primfaktor i venstre kolonne og det nye tal i højre kolonne. Fortsæt sådan, indtil du ikke kan løse mere (tallet i højre kolonne bliver mindre og mindre).

Så for at fortsætte vores eksempel: 3276 ÷ 2 = 1638, så i venstre kolonne skriver vi endnu en 2 og i højre kolonne 1638. 1638 ÷ 2 = 819, så vi skriver 2 og 819 i venstre og højre kolonne.

4. Behandl de ulige tal ved altid at starte med de mindste primtal. For ulige tal kan det mindste primtal afvige, i modsætning til lige tal, hvor 2 altid er det mindste primtal (undtagen 1). Start med primfaktorer som 3, 5, 7, 11 og så videre, indtil du finder en, der er en faktor af dit tal. Dette er den mindste prime faktor.

I vores eksempel ser vi, at 819 er ulige og derfor ikke kan have en primfaktor på 2. Så lad os prøve en anden prime. 819 ÷ 3 = 273 uden rest, så 3 er den mindste primfaktor på 819, og vi fortsætter med 273.

Når du leder efter faktorer, så prøv alle primtal op til kvadratroden af den største faktor, du fandt. Hvis ingen af de tal, du prøver, er en divisor af den største faktor, så er den største divisor i sig selv sandsynligvis primtal, så du er færdig med at faktorisere.

Billede med titlen Faktor et tal Trin 10

5. Fortsæt indtil du når 1. Fortsæt med at finde den mindste primtal af tallene i højre kolonne, indtil du står tilbage med et primtal i den højre kolonne. Dette dividerer du så med sig selv, så tallet kommer frem i venstre kolonne og en "1" i højre kolonne.

Lad os nu afslutte nedbrydningen. se nedenfor for detaljer:

Divider igen med 3: 273 ÷ 3 = 91, ingen rest, så vi skriver 3 og 91.

Lad os prøve en 3`er igen: dette virker ikke for 91, og det virker heller ikke med 5 (det næste primtal), men 91 ÷ 7 = 13 virker uden rest, så vi skriver ned 7 og 13.

Lad os prøve 7 igen: 13 har hverken 7 eller 11 som en faktor, men sig selv: 13 ÷ 13 = 1.Så for at lukke dette bord, bemærker vi 13 og 1. Vi kan endelig stoppe factoring.

Billede med titlen Faktor et tal Trin 11

6. Tallene i venstre kolonne er dine faktorer. Det betyder, at produktet af en multiplikation af disse tal skal være lig med tallet øverst i tabellen. Hvis den samme faktor forekommer mere end én gang, skal du skrive den som en potens af denne faktor for at spare plads. For eksempel, hvis 2`et forekommer fire gange på din liste over faktorer, skal du skrive det som 2 i stedet for 2 × 2 × 2 × 2.

Så i vores eksempel skriver vi som følger: 6552 = 2×3×7×13. Dette er den komplette primfaktorisering af 6552. Så produktet af multiplikationen af disse tal er 6552.

Tips

1-tallet er ikke et primtal, men et specialtilfælde.
De første primtal er 2, 3, 5, 7, 11, 13, 17, 19 og 23.
Forstå, at et tal er en faktor af et andet, større tal, hvis dette tal er deleligt helt med faktoren; altså uden en rest tilbage. For eksempel er tallet 6 en faktor på 24, fordi 24 ÷ 6 = 4, uden rest.6 er derfor ikke en faktor på 25.
Hvis tallene i tælleren summeres til et multiplum af tre, så er tre en faktor af dette tal. (819 = 8+1+9 = 18 = 1+8 =9.Tre er en faktor på ni, så det er også en faktor på 819)
Nogle tal kan faktoriseres hurtigere, men denne måde fungerer altid, og en ekstra fordel er, at primfaktorerne er anført i stigende rækkefølge, når du er færdig.
Husk, at vi kun taler om heltal som 1, 2, 3, 4, 5...og ikke om brøker eller decimaltal, hvilket er uden for rammerne af denne artikel.

Advarsler

Gør det ikke for svært for dig selv. Hvis du har udelukket en faktor, skal du ikke fortsætte med at tjekke i det uendelige. Når du har opdaget, at 2 ikke kan være en faktor på 819, skal du fortsætte med at vide, at du ikke behøver at overveje 2 som en faktor igen.