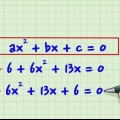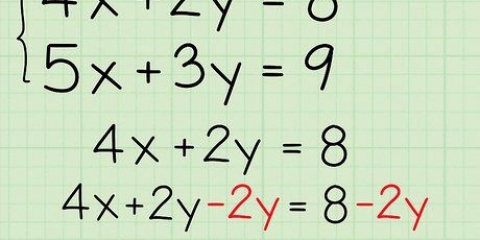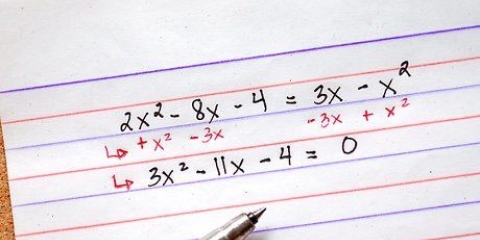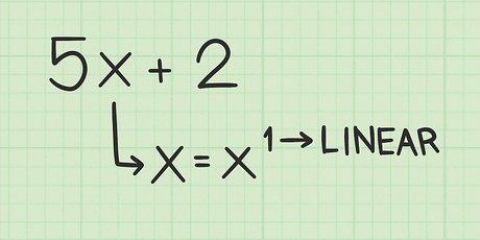Faktorering af et tredjegradspolynomium: 12 trin (med billeder)

Indhold

Trin
- Del 1 af 2: Opløses ved gruppering
- Del 2 af 2: Factoring med friterminen
Tips

Denne artikel handler om faktorisering af et kubisk polynomium, også kaldet et polynomium. Vi skal undersøge, hvordan vi kan gøre dette ved at gruppere og bruge faktorerne i det frie udtryk.

Trin

Del 1 af 2: Opløses ved gruppering

1. Opdel polynomiet i to grupper. At dividere polynomiet hjælper med at løse hver enkelt del.

Antag, at vi arbejder med følgende polynomium:" x + 3x - 6x - 18 = 0. Lad os opdele dette i (x + 3x) og (-6x - 18)

Billede med titlen Faktor et kubisk polynomium Trin 2

2. Prøv at finde ud af, hvad der er det samme i hver gruppe.

Ved (x + 3x) ser vi, at x er lig.

Ved (-6x - 18) ser vi, at -6 er lig.

Billede med titlen Faktor et kubisk polynomium Trin 3

3. Fjern disse lige faktorer fra de to udtryk.

Ved at faktorisere x får vi x(x + 3).

Ved at dekomponere -6 fra det andet stykke får vi -6(x + 3).

Billede med titlen Faktor et kubisk polynomium Trin 4

4. Hvis hvert af de to udtryk indeholder den samme faktor, kan du kombinere disse faktorer.

Dette giver (x + 3)(x - 6).

Billede med titlen Faktor et kubisk polynomium Trin 5

5. Find løsningen ved at se på rødderne. Hvis du har x i en kvadratrod, skal du huske, at både positive og negative tal er gyldige for den ligning.

Løsningerne er -3 og √6.

Del 2 af 2: Factoring med friterminen

Billede med titlen Faktor et kubisk polynomium Trin 6

1. Omarranger udtrykket i følgende form: ax+bx+cx+d.

Antag, at du arbejder med ligningen: x - 4x - 7x + 10 = 0.

Billede med titlen Faktor et kubisk polynomium Trin 7

2. Find alle faktorer af "d". Konstanten "d" bliver tallet uden variabler ved siden af "x".

Faktorer er de tal, som du kan gange sammen for at få et andet tal. I dette tilfælde er disse faktorerne 10 eller "d": 1, 2, 5 og 10.

Billede med titlen Faktor et kubisk polynomium Trin 8

3. Find en faktor, der gør polynomiet lig nul. Vi ønsker at bestemme, hvilken faktor der gør polynomiet lig nul, hvis vi anvender denne faktor for "x" udfyld ligningen.

Start med at bruge den første faktor, 1. erstatning "1" for hver "x" i sammenligningen:
(1) - 4(1) - 7(1) + 10 = 0

Dette giver: 1 - 4 - 7 + 10 = 0.

Da 0 = 0 er et sandt udsagn, ved du, at x = 1 er løsningen.

Billede med titlen Faktor et kubisk polynomium Trin 9

4. Gå nu og omarranger alt. Hvis x=1 så er det muligt at skrive denne ligning lidt anderledes uden at ændre betydningen.

"x = 1" er det samme som "x - 1 = 0" eller "(x - 1)". Du har kun én "1" trækkes fra hver side af ligningen.

Billede med titlen Faktor et kubisk polynomium Trin 10

5. Faktorer kvadratroden af ligningen ud. "(x - 1)" er roden. Prøv at tage disse ud af resten af ligningen. Gør dette med et polynomium ad gangen.

Kan du faktorisere (x - 1) fra x? Nej det er ikke muligt. Men hvis du først låner a -x fra den anden variabel: x(x - 1) = x - x.

Kan du faktorisere (x - 1) fra, hvad der er tilbage af den anden variabel? Nej, det er heller ikke muligt her. Du skal låne noget fra den tredje variabel igen, som er 3x af -7x. Dette giver os -3x(x - 1) = -3x + 3x.

Da du tog 3x ud af -7x, er den tredje variabel nu -10x, og konstanten er 10. Kan du frigøre dette. Ja selvfølgelig! -10(x - 1) = -10x + 10.

Det du har gjort er at omarrangere variablerne, så du kan få faktoren (x - 1) fra hele ligningen. Den modificerede ligning ser sådan ud: x - x - 3x + 3x - 10x + 10 = 0, men er stadig den samme som x - 4x - 7x + 10 = 0.

Billede med titlen Faktor et kubisk polynomium Trin 11

6. Fortsæt med at erstatte faktorerne i den frie periode. Se på de tal, du løste ved hjælp af (x - 1) i trin 5:

x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Du kan omarrangere disse for at gøre det nemmere at opløse igen: (x - 1)(x - 3x - 10) = 0.

Her prøver du bare at faktorisere (x - 3x - 10). Faktorerne bliver så (x + 2)(x - 5).

Billede med titlen Faktor et kubisk polynomium Trin 12

7. Din løsning er de faktoriserede rødder. Tjek denne løsning ved at indsætte hver af dem tilbage i den oprindelige ligning.

(x - 1)(x + 2)(x - 5) = 0 Dette giver løsningerne for 1, -2 og 5.

Indsæt -2 i ligningen: (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0.

Indsæt 5 i ligningen: (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.

Tips

Den kubiske ligning er produktet af 3 førstegradsligninger eller af en førstegradsligning og en andengradsligning, der ikke kan faktoriseres. I sidstnævnte tilfælde, efter at have fundet førstegradspolynomiet, bruger du lang division til at finde andengradspolynomiet.
Der er ingen kubiske polynomier, der ikke kan faktoriseres, når det kommer til reelle tal, fordi denne ligning skal have en kvadratrod af reelle tal. Tredjegradsligninger såsom x + x + 1, der har en irrationel reel rod, kan ikke indregnes i polynomier med heltal eller rationelle tal som koefficient. Selvom det kan indregnes i selve ligningen, kan det ikke reduceres til et heltalspolynomium.

Metode 2 svarer til lang division af to polynomier, en.v:

(x-1) ∕x³ - 4x²-7x+10 ∕

- 10x + 10................= (x-1) (-10)

Betingelserne x², -3x og -10 af kvotienten opnås ved altid at trække det 1. led af divisoren ( x ) fra det første led af dividenden, eller hvad der er tilbage af det ( x³, -3x², -10x ).