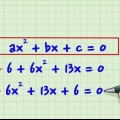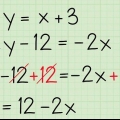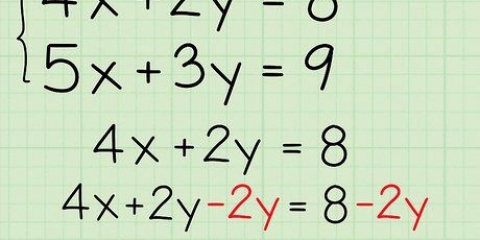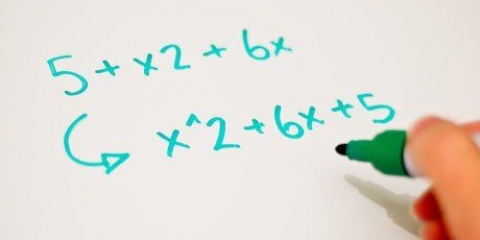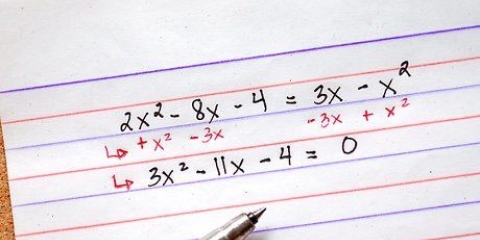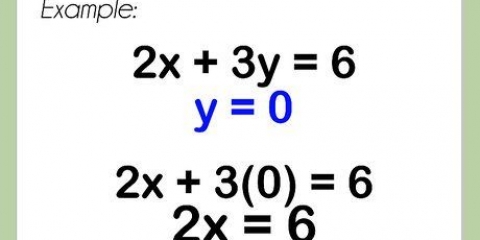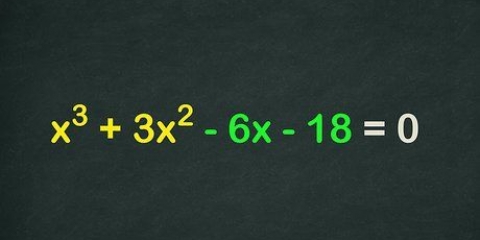Factoring Equations

Indhold

Trin
Tips
Fornødenheder

I matematik er det faktorisere at bestemme tal eller udtryk, der, når de ganges sammen, giver en bestemt værdi eller ligning. Factoring er en nyttig færdighed at lære, når man løser simple matematiske problemer; evnen til at faktorisere korrekt bliver næsten afgørende, når man beskæftiger sig med andengradsligninger og andre polynomier. Factoring kan bruges til at forenkle simple matematiske ligninger for at gøre det nemmere at løse dem. Factoring kan give dig mulighed for selv at udelukke mulige svar meget hurtigere, end hvis du skulle tjekke hver enkelt af dem.

Trin

Metode 1 af 3: Faktorisering af tal og simple ligninger

1. Forstå definitionen af faktorisering i tal. Factoring er i princippet simpelt, men i praksis kan det være ret udfordrende, når man skal løse komplekse ligninger. Derfor er den enkleste tilgang at starte med små tal og derefter simple ligninger, før du går videre til mere avancerede applikationer. Det faktorer af et givet tal er de tal, der ganget sammen giver det enkelte tal. For eksempel er faktorerne for 12 1, 12, 2, 6, 3 og 4, fordi 1 × 12, 2 × 6 og 3 × 4 alle har 12 som deres produkt.

En anden måde at tænke dette på er, at faktorerne for et givet tal er de tal, der gør tallet ind kan deles i sin helhed.
Kan du finde alle faktorer på 60? Vi bruger tallet 60 til forskellige applikationer (antal minutter i en time, sekunder i et minut osv.), fordi det er deleligt med et stort sæt tal.

Faktorerne på 60 er 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 og 60.

Billede med titlen Factor Algebraic Equations Trin 2

2. Forstå, at ligninger også kan tages i betragtning. Ligesom tal kan variabler med koefficienter også faktoriseres. Det gør du ved at finde faktorerne for variablens koefficient. At vide, hvordan man faktoriserer variabler, er nyttigt til at forenkle ligninger, som variablerne er en del af.

For eksempel kan variablen 12y omskrives som produktet af faktorerne 12 og y. Vi kan skrive 12y som 3(4y), 2(6y) osv., ved at bruge de faktorer på 12, der er mest bekvemme.

Vi kan endda gå så langt som 12 år flere gange opløse. Med andre ord, vi behøver ikke at stoppe ved 3(4y) eller 2(6y) - vi kan faktorisere 4y og 6y til henholdsvis 3(2(2y) og 2(3(2y)). Tilsyneladende svarer disse to udtryk til hinanden.

Billede med titlen Factor Algebraic Equations Trin 3

3. Anvend den fordelende egenskab ved multiplikation til faktorisering af matematiske ligninger. Ved at bruge din viden om, hvordan du faktoriserer både regulære tal og variabler med koefficienter, kan du også forenkle matematiske ligninger ved at bestemme de faktorer, der er fælles for tal og variable i en matematisk ligning. Normalt vil vi forenkle ligningen så meget som muligt ved at lede efter den største fælles divisor (gcd). Denne forenklingsproces er mulig på grund af multiplikationens fordelingsegenskab, som siger, at for ethvert tal a, b og c, a(b + c) = ab + ac.

Lad os prøve et eksempel på et problem. For at faktorisere ligningen 12x + 6, ser vi først efter gcd`en for 12x og 6. 6 er det største tal, der deler både 12x og 6, så vi kan forenkle ligningen til 6(2x + 1).

Denne proces gælder også for ligninger, der involverer negative tal og brøker. x/2 + 4 kan for eksempel simplificeres til 1/2(x + 8) og -7x + -21 kan indregnes i -7(x + 3).

Metode 2 af 3: Faktorisering af andengradsligninger

Billede med titlen Factor Algebraic Equations Trin 4

1. Sørg for, at ligningen er i andengradsform (ax + bx + c = 0). andengradsligninger har formen ax + bx + c = 0, hvor a, b og c er numeriske konstanter og a ikke er lig med 0 (bemærk at a er lig med kan er på 1 eller -1). Hvis du har at gøre med en ligning med en variabel (x) og et eller flere led af x i anden kvadrat, kan du normalt bytte ligningens led ved hjælp af en standard matematisk operation for at få 0 på den ene side af ligningen. skilt og økse mv. på den anden side.

For eksempel har du følgende matematiske ligning: 5x + 7x - 9 = 4x + x - 18, som kan simplificeres til x + 6x + 9 = 0, i andengradsformen.
Ligninger med større potens af x, såsom x, x osv. er ikke andengradsligninger. Disse er kubiske ligninger eller højere, medmindre ligningen kan forenkles, så led med højere potenser af x(end kvadrater) elimineres.

Billede med titlen Factor Algebraic Equations Trin 5

2. I andengradsligninger, hvor a = 1, indregnes i (x+d )(x+e), hvor d × e = c og d + e = b. Hvis din andengradsligning har formen x + bx + c = 0 (med andre ord, hvis koefficienten for x = 1), så er det muligt (men ikke sikkert), at en relativt simpel genvej kan bruges til at faktorisere ligningen. Find to tal, der begge har c som produkt og læg dem sammen for at få b som en sum. Hvis du har disse to tal d og e, skal du sætte dem i følgende udtryk: (x+d)(x+e). Disse to led, når de ganges, giver dig andengradsligningen - med andre ord, de er faktorerne i din andengradsligning.

Tag for eksempel andengradsligningen x + 5x + 6 = 0. Da 3 x 2 = 6 og 3 + 2 = 5, bliver den forenklede ligning (x + 3)(x + 2).

Små variationer af denne enkle hurtige løsning kan findes i selve ligningen:

Hvis andengradsligningen har formen x-bx+c, vil dit svar se sådan ud: (x - _)(x - _).

Hvis af formen x+bx+c, så vil dit svar se sådan ud: (x + _)(x + _).

Hvis af formen x-bx-c, vil dit svar se således ud: (x + _)(x - _).

Bemærk: De tomme felter kan være brøker eller decimaler. For eksempel, ligningen x + (21/2)x + 5 = 0 faktorer i (x + 10)(x + 1/2).

Billede med titlen Factor Algebraic Equations Trin 6

3. Hvis det er muligt, kan du også opløse faktorerne ved blot at se nøje efter. Tro det eller ej, du kan løse simple andengradsligninger blot ved at se på problemet nøje, og så veje de mulige svar, indtil du finder den rigtige. Med andre ord, nedbrydes til faktorer ved at prøve. Hvis ligningen har formen ax+bx+c og a>1, så vil vilkårene have formen (dx +/- _)(ex +/- _), hvor d og e er konstanter, større end nul, som ganget sammen har a som produkt. Både d og e (eller begge) kan lig med 1, men det er ikke altid tilfældet. Hvis begge er 1, så har du i det væsentlige brugt den hurtige metode beskrevet ovenfor.

Lad os udarbejde en eksempelopgave. 3x - 8x + 4 virker lidt skræmmende i starten. Men hvis vi indser, at 3 kun har to faktorer (3 og 1), så bliver det meget nemmere, fordi vi ved, at vores svar skal have formen (3x +/- _)(x +/- _). I dette tilfælde vil indtastning af -2 i de tomme felter give det rigtige svar. -2 × 3x = -6x og -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, så vi ser, at termerne i parentes ganget sammen har den oprindelige ligning som produktet.

Billede med titlen Factor Algebraic Equations Trin 7

4. Løs dette ved at kvadrere. I nogle tilfælde kan andengradsligninger faktoriseres hurtigt og nemt ved at bruge en speciel matematisk egenskab. Enhver andengradsligning på formen x + 2xh + h = (x + h). Så hvis værdien for b i din ligning er det dobbelte af kvadratroden af c, så kan din ligning indregnes i (x + (sqrt(c))).

For eksempel opfylder ligningen x + 6x + 9 denne form. 3 er 9 og 3 × 2 er 6. Så vi ved, at faktorerne i denne ligning er lig med (x + 3)(x + 3) eller (x + 3).

Billede med titlen Factor Algebraic Equations Trin 8

5. Brug faktorer til at løse andengradsligninger. Uanset hvordan du faktoriserer en andengradsligning; når den er indregnet, kan du finde de mulige svar for værdien for x ved at sætte hver faktor lig med nul og løse for den. Da du leder efter værdier for x, hvor din ligning er nul, vil en værdi for x, der gør hver faktor lig med nul, være det mulige svar på din andengradsligning.

Lad os vende tilbage til ligningen x + 5x + 6 = 0. Den løste ligning er (x + 3)(x + 2) = 0. Hvis en af disse faktorer er lig med 0, så er hele ligningen 0, så de mulige svar for x er de tal, hvor (x + 3) og (x + 2) er lig med 0. Disse tal er henholdsvis -3 og -2.

Billede med titlen Factor Algebraic Equations Trin 9

6. Tjek dine svar – nogle af dem kan være forkerte! Når du har fundet de mulige svar for x, skal du anvende dem tilbage på din oprindelige ligning for at se, om de er gyldige. Nogle gange vil de svar, du finder, være den oprindelige ligning ikke gøre lig med nul, når du anvender dem. Disse svar er ukorrekt og vi ignorerer dem.

Vi anvender -2 og -3 til x + 5x + 6 = 0. Først ud: -2:

(-2) + 5(-2) + 6 = 0

4 + -10 + 6 = 0

0 = 0. Dette er korrekt, så -2 er et gyldigt svar.

Nu prøver vi -3:

(-3) + 5(-3) + 6 = 0

9 + -15 + 6 = 0

0 = 0. Dette er også korrekt, så -3 er også et gyldigt svar.

Metode 3 af 3: Faktorering af andre ligningsformer

Billede med titlen Factor Algebraic Equations Trin 10

1. Hvis ligningen har formen a-b, så er de faktoriserede led (a+b)(a-b). Ligninger af to variable løses anderledes end andengradsligninger. For enhver ligning a-b, hvor a og b ikke er lig med 0, er ligningens faktorer (a+b)(a-b).

For eksempel ligningen 9x - 4y = (3x + 2y)(3x - 2y).

Billede med titlen Factor Algebraic Equations Trin 11

2. Hvis ligningen har formen a+2ab+b, nedbrydes den i (a+b). Bemærk: med a trinomialet af formen a-2ab+b, den opløste form er lidt anderledes: (a-b).

Ligningen 4x + 8xy + 4y kan omskrives til 4x + (2 × 2 × 2)xy + 4y. Nu står det klart, at det er i den rigtige form, så vi med en vis tillid kan konstatere, at vores ligning kan indregnes i (2x + 2y).

Billede med titlen Factor Algebraic Equations Trin 12

3. Hvis ligningen har formen a-b, så dekomponerer du den til (a-b)(a+ab+b). Til sidst skal det nævnes, at kubiske ligninger og højere polynomier også kan faktoriseres, selvom denne proces hurtigt bliver ubrugelig kompliceret.

For eksempel: 8x - 27y kan indregnes i (2x - 3y)(4x + ((2x)(3y)) + 9y).

Tips

a-b kan faktoriseres, men a+b kan ikke.
Lær, hvordan du faktoriserer konstanter – dette kan hjælpe.
Pas på brøker under faktoriseringen og regn dem ud korrekt og omhyggeligt.
Hvis du har et trinomium af formen x+bx+ (b/2), så er den faktoriserede form (x+(b/2)) (du kan støde på dette med en kvadratisk formel).
Husk at a x 0 = 0.