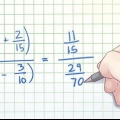
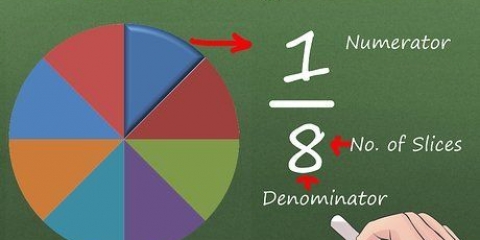
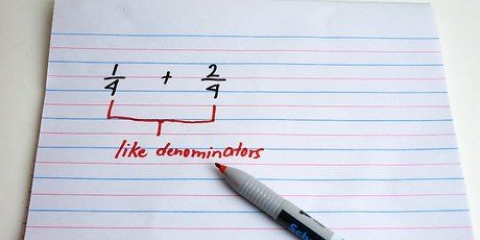
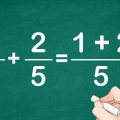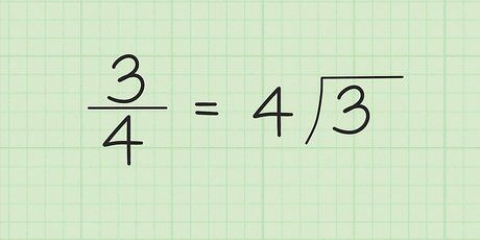(/2) = /2 × /2 eller (/2). Kvadring af hvert tal giver (/4). 
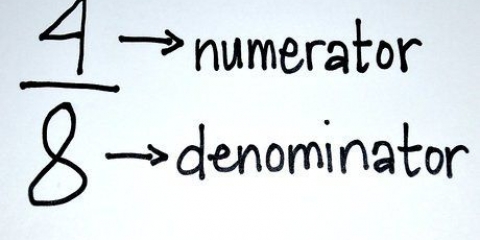
Tælleren forbliver oven på brøken, og nævneren forbliver i bunden. For eksempel: (/2) = (/2 x 2) = (/4). 
For at konvertere dette til et blandet tal skal du dividere 25 med 4. Dette er 6 (6 x 4 = 24), med en rest på 1. Derfor er det blandede tal 6/4. 

For eksempel: (-/4) = (–/4) x (-/4) 
For eksempel: (-2) x (-8) = (+16) 
Hvis vi fortsætter med eksemplet, vil den resulterende brøk være et positivt tal. (–/4) x (-/4) = (+/16) Skikken er at udelade plustegnet fra positive tal. 
For eksempel: (/16) har en fælles faktor på fire. Divider brøken med 4: 4/4 = 1, 16/4 = 4 Omskriv den forenklede brøk: (/4) 

For eksempel: 16 × (/16) Kvadret parenteserne og eliminer den fælles faktor på 16: 16 * /16 * /16 Da du her har at gøre med en 16`er som et heltal og to gange en 16`er i nævneren, kan du eliminere en af dem. Omskriv den forenklede ligning: 12 × /16 forenkle /16 ved at dividere med 4: /4 Multiplicer: 12 × /4 = 36/4 Del: 36/4 = 9 
For eksempel: 16 * (/16) Omskriv med kvadreret tæller og nævner: 16 * (/16) Træk eksponenten fra i nævneren: 16 * /16 Forestil dig de første 16 som en eksponent for 1:16. Ved at bruge reglerne for at trække potenser/eksponenter trækker man eksponenterne fra hinanden. 16/16, giver 16 = 16 eller 1/16. Nu fortsætter du med /16 Omskriv og forenkle brøken: /16 =* /4. Forenklet: 12 × /4 = 36/4 Del: 36/4 = 9
Kvadreringsbrøker
Indhold
Kvadring af brøker er en af de enkleste operationer, du kan udføre på brøker. Det minder meget om at kvadrere heltal, idet du bare kan gange både tælleren og nævneren med sig selv. Der er nogle tilfælde, hvor forenkling af fraktionen før kvadrering gør proceduren lettere. Hvis du endnu ikke har lært denne færdighed, giver denne artikel et kort overblik for at forbedre din forståelse.
Trin
Del 1 af 3: Kvadring af brøker

1. Forstå, hvordan man kvadrater heltal. Når du ser et tal hævet til anden potens, ved du at kvadrere tallet. Dette er det samme som at gange tallet med sig selv. For eksempel:
- 5 = 5 × 5 = 25

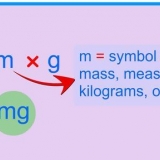
2. Er du klar over, at kvadraturbrøker fungerer på samme måde. For at kvadrere en brøk skal du gange brøken med sig selv. En anden måde at tænke på dette er at gange tælleren med sig selv og nævneren med sig selv. For eksempel:

3. Multiplicer tælleren med sig selv og nævneren med sig selv. Den faktiske rækkefølge, hvori du multiplicerer disse tal med sig selv, er ligegyldigt, så længe du kvadrerer begge tal. For at gøre tingene enkle, start med tælleren: multiplicer den med sig selv. Gang derefter nævneren med sig selv.

4.Forenkle brøkdelen for at afslutte dette. Når man beskæftiger sig med brøker, er det sidste trin altid at forenkle brøken til dens simpleste form eller konvertere en uægte brøk til et blandet tal. Vores eksempel, /4 er en uægte brøk, fordi tælleren er større end nævneren.
Del 2 af 3: Kvadring af brøker med negative tal

1. Se efter et minustegn foran brøken. Hvis du har med en negativ brøk at gøre, er der et minustegn foran den. Det er klogt altid at sætte parentes omkring et negativt tal, så du ved, at minustegnet refererer til tallet og ikke er ment som en minussum.
- For eksempel: (-/4)

2. Gang brøken med sig selv. Kvaddre brøken, som du normalt ville, ved at gange tælleren med sig selv og derefter gange nævneren med sig selv. Du kan også bare gange brøken med sig selv.

3. Forstå, at gange to negative tal sammen giver et positivt tal. Når et minustegn er til stede, bliver hele brøken negativ. Når du kvadrerer brøken, gange du to negative tal. Når to negative tal ganges sammen, er produktet altid positivt.

4. Fjern minustegnet efter firkantering. Hvis du har kvadreret brøken, har du ganget to negative tal. Det betyder, at den kvadratiske brøk er positiv. Glem ikke at udelade minustegnet i det endelige svar.

5. Forenkle brøken så vidt muligt. Det sidste trin i at lave brøkberegninger er at forenkle. Uægte brøker skal først simplificeres til blandede tal og derefter yderligere simplificeres.
Del 3 af 3: Brug af forenklinger og hurtige løsninger

1. Tjek om du kan lave brøkenforenkle før du firer det. Det er normalt nemmere at forenkle brøker før kvadrering. Husk, at forenkling af en brøk involverer at dividere den med en fælles faktor, indtil 1 er det eneste tal tilbage, der kan divideres med både tælleren og nævneren. At forenkle en brøk først betyder, at du ikke behøver at forenkle den igen til sidst, når tallene er større.
- For eksempel: (/16)
- 12 og 16 kan begge divideres med 4. 12/4 = 3 og 16/4 = 4; så du kan/16 forenkle til /4.
- Nu kan du lave brøken /4 til kvadrat.
- (/4) = /16, som du ikke kan forenkle længere.
- For at bevise dette kvadrerer vi den oprindelige brøk uden at forenkle:
- (/16) = (/16x16) = (/256)
- (/256) har en fælles faktor på 16. At dividere både tælleren og nævneren med 16 forenkler brøken til (/16), den samme brøk, som vi fik ved at forenkle først.

2. Lær, hvornår du skal vente med at forenkle en brøkdel. Har du at gøre med mere komplekse ligninger, så kan det være muligt at eliminere en af faktorerne. I et sådant tilfælde er det derfor mere bekvemt at vente med at forenkle fraktionen. Tilføjelse af en ekstra faktor til ovenstående eksempel gør dette klarere.

3. Forstå, hvordan du gør dette hurtigt medeksponent. En anden måde at løse det samme problem på er først at forenkle eksponenten. Resultatet vil være det samme, kun opnået gennem en anden rute.
Fornødenheder
- Papir eller en computer
- Blyant/pen (hvis du bruger papir)
Artikler om emnet "Kvadreringsbrøker"
Оцените, пожалуйста статью
Populær