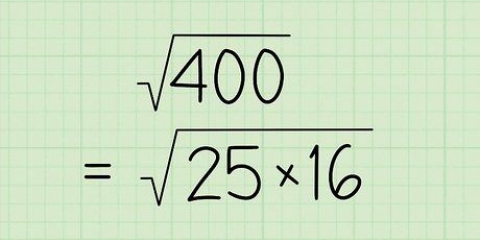Sådan beregnes afstanden mellem to punkter: 6 trin (med billeder)

Indhold

Trin
Tips

Tænk på afstanden mellem to punkter som en linje. Længden af denne linje kan findes ved hjælp af afstandsformlen: $\sqrt{(} (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2})$ ${sqrt(}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})$ .

Trin

1. Tag koordinaterne for to punkter, som du vil finde afstanden imellem. Kald det ene punkt 1 (x1,y1) og det andet punkt 2 (x2,y2). Det er lige meget, hvilket punkt du starter fra, så længe du anvender etiketterne (1 og 2) konsekvent gennem hele problemet.

x1 er den vandrette koordinat (langs x-aksen) for punkt 1, og x2 er den vandrette koordinat for punkt 2. y1 er den lodrette koordinat (langs y-aksen) for punkt 1, og y2 er den lodrette koordinat af punkt 2.
Nej, for eksempel punkterne (3.2) og (7.8). Hvis (3.2) er lig med (x1,y1), så er (7.8) lig med (x2,y2).

Billede med titlen Find afstanden mellem to punkter Trin 1

2. Brug afstandsformlen. Denne formel bestemmer længden af en ret linje mellem to punkter: punkt 1 og punkt 2. Den lineære afstand er kvadratroden af kvadratet af den vandrette afstand, plus kvadratet af den lodrette afstand mellem to punkter. Kort sagt er det kvadratroden af:

(x 2 - x_{1})^{2} + (y_{2} - y_{1})^{2}

$(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Billede med titlen Find afstanden mellem to punkter Trin 3

3. Bestem den vandrette og lodrette afstand mellem punkterne. Beregn først y2 - y1 for at finde den lodrette afstand. Beregn derefter x2 - x1 for at finde den vandrette afstand. Bare rolig, hvis subtraktionen giver negative tal. Det næste trin er at kvadrere disse værdier (hvilket altid resulterer i et positivt heltal).

Bestem afstanden langs y-aksen. For eksemplet punkt (3.2) og (7.8), hvor punkt 1 er (3.2) og punkt 2 (7.8), bliver dette: (y2 - y1) = 8 - 2 = 6. Det betyder, at afstanden på y-aksen mellem disse to punkter er seks længdeenheder.

Bestem afstanden langs x-aksen. For de samme prøvepunkter (3.2) og (7.8): (x2 - x1) = 7 - 3 = 4. Det betyder, at der er fire længdeenheder, der adskiller de to punkter på x-aksen.

Billede med titlen Find afstanden mellem to punkter Trin 4

4. Kvadret begge værdier. Det betyder, at du kvadrerer x-aksens afstand (x2 - x1), og du kvadrerer y-aksens afstand (y2 - y1).

62 = 36

$6^{2}=36$

42 = 16

$4^{2}=16$

Billede med titlen Find afstanden mellem to punkter Trin 5

5. Læg firkanterne sammen. Dette vil give dig kvadratet af den diagonale, lineære afstand mellem dine to punkter. I eksemplet med punkt (3.2) og (7.8) er kvadratet af (7 - 3) 16, og kvadratet af (8 - 2) er 36. 36 + 16 = 52.

Billede med titlen Find afstanden mellem to punkter Trin 6

6. Tag kvadratroden af ligningen. Dette er det sidste trin i ligningen. Den lineære afstand mellem de to punkter er kvadratroden af summen af kvadraterne af afstanden på x-aksen og afstanden på y-aksen.

Hvis vi fortsætter med eksemplet, er afstanden mellem (3.2) og (7.8) kvadratroden af 52 eller cirka 7.21.

Tips

Det er lige meget, om du får et negativt tal efter at have trukket y2 - y1 eller x2 - x1 fra. Fordi forskellen er kvadratisk får du altid en positiv afstand i dit svar.