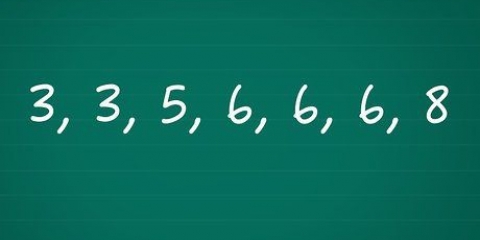Beregning af kovarians

Indhold

Trin
Advarsler

Kovarians er en statistisk beregning for at gøre forholdet mellem to sæt data mere gennemsigtigt. Antag for eksempel, at antropologer studerer højden og vægten af en befolkning inden for en bestemt kultur. For hver person i undersøgelsen kan højde og vægt repræsenteres med et datapar (x, y). Disse værdier kan bruges i en standardformel til beregning af kovariansrelationen. Denne artikel forklarer først beregningerne til at bestemme kovariansen af et datasæt. Dernæst vil to andre automatiserede måder at bestemme resultatet på blive diskuteret.

Trin

Metode 1 af 4: Beregning af kovariansen i hånden ved hjælp af standardformlen

1. Lær standard kovariansformlen og dens dele. Standardformlen til beregning af kovariansen er

Σ (x jeg - x_{gns}) (y_{jeg} - y_{gns}) / (n - 1)

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})/(n-1)$ . For at bruge denne formel skal du kende betydningen af variablerne og symbolerne:

$Σ$ $Sigma$ - Dette symbol er det græske bogstav `sigma`. I matematiske funktioner betyder det at tilføje en række af det, der følger. I denne formel betyder Σ-tegnet, at du beregner værdierne i brøkens tæller, lægger dem alle sammen, og dividerer derefter totalen med nævneren.
$x jeg$ $x_{i}$ - Du kan læse denne variabel som `x sub i`. Sænkningen i repræsenterer en tæller. Det betyder, at du skal lave en beregning for hver værdi af x i dit datasæt.
$x -en v g$ $x_{{gennemsnit}}$ - `avg` angiver, at x(avg) er middelværdien af alle x datapunkter. Middelværdien skrives nogle gange som et x med en kort vandret linje over sig. I den stil læser du variablen som `x-bar`, men det betyder stadig gennemsnittet af datasættet.
$y jeg$ $y_{i}$ - Du kan læse denne variabel som `y sub i`. Underskriften i er tælleren. Det betyder, at du skal lave en beregning for hver værdi af y i dit datasæt.
$y -en v g$ $y_{{gennemsnit}}$ - `avg` angiver, at y(avg) er middelværdien af alle x datapunkter. Middelværdien skrives nogle gange som et y med en kort vandret linje over sig. I den stil læser du variablen som `y-bar`, men det betyder stadig gennemsnittet af datasættet.
$n$ $n$ - Denne variabel er antallet af elementer i dit datasæt. Husk, at i et kovariansproblem er et enkelt `element` sammensat af både en x-værdi og en y-værdi. Værdien `n` er antallet af par af datapunkter, ikke individuelle tal.

Billede med titlen Beregn kovarians Trin 2

2. Konstruer din datatabel. Før du går i gang, er det nyttigt at indsamle dine data. Opret en tabel med fem kolonner. Du skal deklarere hver kolonne som følger:

x

$x$ - Udfyld denne kolonne med værdierne af punkterne i x-dataene.

y

$y$ - Udfyld denne kolonne med værdierne af y-dataene. Sørg for, at y-værdierne er justeret med de tilsvarende x-værdier. I et kovariansproblem er rækkefølgen af datapunkterne og koblingen af x og y vigtig.

(x jeg - x_{gns})

$(x_{i}-x_{{text{avg}}})$ - Lad denne kolonne være tom i begyndelsen. Du kommer til at fylde det med data, efter du har beregnet gennemsnittet af x-dataene.

(y jeg - y_{gns})

$(y_{i}-y_{{text{avg}}})$ - Lad denne kolonne være tom i begyndelsen. Du kommer til at udfylde den med data, efter du har beregnet gennemsnittet af y-dataene.

Produkt

${text{Produkt}}$ - Lad også den sidste kolonne være tom. Dette vil blive udfyldt under behandlingen af opgaven.

Billede med titlen Beregn kovarians Trin 3

3. Beregn middelværdien af x datapunkter. Denne prøvedataindsamling indeholder 9 numre. For at finde gennemsnittet skal du lægge dem sammen og dividere summen med 9. Dette giver resultatet 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. Når du dividerer dette med 9, får du gennemsnittet 4,89. Dette er den værdi, du vil bruge som x(avg) til de kommende beregninger.

Billede med titlen Beregn kovarians Trin 4

4. Beregn middelværdien af y-datapunkterne. Denne y-kolonne skal også bestå af 9 datapunkter, der falder sammen med de x datapunkter. Bestem gennemsnittet af dette. For dette eksempeldatasæt bliver det 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Divider denne total med 9 for at få et gennemsnit på 5,44. Du vil bruge 5,44 som værdien af y(avg) til de kommende beregninger.

Billede med titlen Beregn kovarians Trin 5

5. Beregn værdierne (xjeg-xgns){displaystyle (x_{i}-x_{text{avg}})} $(x_{i}-x_{{text{avg}}})$ . For hvert element i x-kolonnen skal du beregne forskellen mellem dette tal og middelværdien. For dette eksempelproblem betyder det at trække 4,89 fra hver x-værdi. Hvis det oprindelige datapunkt er mindre end gennemsnittet, vil dit resultat være negativt. Hvis det oprindelige datapunkt er større end middelværdien, vil resultatet være positivt. Sørg for at holde styr på, hvilke værdier der er negative.

For eksempel er det første datapunkt i x-kolonnen 1. Værdien, der skal indtastes på den første linje i kolonnen

(x jeg - x_{gns})

$(x_{i}-x_{{text{avg}}})$ er: 1 – 4,89 = -3,89.

Gentag denne proces for hvert datapunkt. Så den anden linje bliver: 3 - 4,89 = -1.89. Den tredje linje bliver: 2 - 4,89 = -2,89. Fortsæt denne proces for alle datapunkter. De ni tal i denne kolonne bliver: -3,89, -1,89, -2,89, 0,11, 3,11, 2,11, 7,11, -2,89, -0,89.

Billede med titlen Beregn kovarians Trin 6

6. Beregn værdierne (yjeg-ygns){displaystyle (y_{i}-y_{text{avg}})} $(y_{i}-y_{{text{avg}}})$ . I denne kolonne skal du foretage lignende subtraktioner ved at bruge y-datapunkterne og y-middelværdien. Hvis det oprindelige datapunkt er mindre end middelværdien, vil resultatet være negativt. Hvis det oprindelige datapunkt er større end gennemsnittet, vil dit resultat være positivt. Sørg for at holde styr på, hvilke værdier der er negative.

Så for den første linje vil din beregning være: 8 -5,44, = 2,56.

Den anden linje bliver: 6 – 5,44 = 0,56.

Fortsæt med at trække værdierne fra indtil slutningen af datalisten. Når du er færdig, skal du have følgende ni værdier i denne kolonne: 2,56, 0,56, 3,56, -1,44, -2,44, -2,44, -3,44 , 1,56, 1,56.

Billede med titlen Beregn kovarians Trin 7

7. Beregn produkterne for hver datarække. Du udfylder rækkerne i den sidste kolonne ved at gange de tal, du beregnede i de to foregående kolonner af

(x jeg - x_{gns})

$(x_{i}-x_{{text{avg}}})$ og

(y jeg - y_{gns})

$(y_{i}-y_{{text{avg}}})$ . Arbejd dig vej række for række, og gange de to tal med deres tilsvarende datapunkter. Pas på eventuelle negative værdier undervejs.

I den første række af disse eksempeldata er

(x jeg - x_{gns})

$(x_{i}-x_{{text{avg}}})$ du beregnede -3,89, og den

(y jeg - y_{gns})

$(y_{i}-y_{{text{avg}}})$ værdi 2,56. Produktet af disse to tal er: -3,89 x 2,56 = -9,96.

For den anden række skal du gange de to tal: -1,88 x 0,56 = -1,06.

Fortsæt med at gange række for række indtil slutningen af datasættet. Når du er færdig, skal de ni værdier i denne kolonne være: -9.96, -1.06, -10.29, -0.16, -7.59, -5.15, -24.46 , -4.51, -1.39.

Billede med titlen Beregn kovarians Trin 8

8. Find summen af værdierne i den sidste kolonne. Det er her Σ-symbolet kommer ind. Efter at have udført alle beregningerne indtil videre, læg resultaterne sammen. For dette eksempeldatasæt skal du nu have ni værdier i den sidste kolonne. Læg de ni tal sammen. Vær meget opmærksom på, om et tal er positivt eller negativt.

Summen af dette eksempeldatasæt skulle summere til -64,57. Skriv denne total i feltet nederst i kolonnen. Dette er værdien af tælleren for standardkovariansformlen.

Billede med titlen Beregn kovarians Trin 9

9. Beregn nævneren for kovariansformlen. Tælleren for standardkovariansformlen er den værdi, du lige har beregnet. Nævneren er repræsenteret af (n-1) og er én mindre end antallet af datapar i dit datasæt.

I dette eksempelproblem er der ni par data, så n er 9. Derfor er værdien af (n-1) lig med 8.

Billede med titlen Beregn kovarians Trin 10

10. Divider tælleren med nævneren. Det sidste trin i beregningen af kovariansen er at dividere tælleren,

Σ (x jeg - x_{gns}) (y_{jeg} - y_{gns})

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})$ ved nævneren,

(n - 1)

$(n-1)$ . Kvoten er kovariansen af dine data.

For dette eksempeldatasæt er denne beregning: -64,57/8 = -8,07.

Metode 2 af 4: Beregn kovarians ved hjælp af et Excel-regneark

Billede med titlen Beregn kovarians Trin 11

1. Læg mærke til, hvad de gentagne beregninger er. Kovarians er en beregning, som du skal lave i hånden et par gange, så du forstår meningen med resultatet. Men hvis du rutinemæssigt skal bruge kovarians til at fortolke data, så har du brug for en hurtigere og automatiseret måde at få resultaterne. Du har måske nu bemærket, at med vores relativt lille datasæt på kun ni par data, bestod beregningerne af to gennemsnit, atten separate subtraktioner, ni multiplikationer, en addition og til sidst endnu en division. Det er 31 relativt små beregninger for at finde løsningen. Undervejs risikerer du at gå glip af negative tegn eller at kopiere resultaterne forkert, så svaret bliver forkert.

Billede med titlen Beregn kovarians Trin 12

2. Opret et regneark til beregning af kovariansen. Hvis du er fortrolig med Excel (eller ethvert andet beregningsprogram), kan du nemt oprette en tabel til bestemmelse af kovariansen. Mærk overskrifterne i de fem kolonner som i de manuelle beregninger: x, y, (x(i)-x(avg)), (y(i)-y(avg)) og produkt.

For at forenkle navngivningen skal du navngive den tredje kolonne noget som "x forskel" og den fjerde kolonne "y forskel", så længe du husker betydningen af dataene.

Hvis tabellen starter i øverste venstre hjørne af regnearket, vil celle A1 blive mærket x, mens de andre etiketter fortsætter til celle E1.

Billede med titlen Beregn kovarians Trin 13

3. Udfyld datapunkterne. Indtast dataværdierne i de to kolonner x og y. Husk, at rækkefølgen af datapunkterne har betydning, så du skal matche hver y med den tilsvarende værdi af x.

X-værdierne starter i celle A2 og fortsætter op til det antal datapunkter, du har brug for.

Y-værdierne starter i celle B2 og fortsætter op til det antal datapunkter, du har brug for.

Billede med titlen Beregn kovarians Trin 14

4. Bestem middelværdierne for x- og y-værdierne. Excel beregner gennemsnittet for dig meget hurtigt. I den første tomme celle under hver kolonne med data skal du skrive formlen =AVERAGE(A2:A___). Udfyld det tomme felt med nummeret på den celle, der svarer til dit sidste datapunkt.

For eksempel, hvis du har 100 datapunkter, vil cellerne A2 til A101 blive udfyldt, så i cellen skal du skrive: = AVERAGE(A2:A101).

For y-dataene skal du indtaste formlen = AVERAGE(B2:B101).

Husk, at en formel i Excel starter med et `=`-tegn.

Billede med titlen Beregn kovarians Trin 15

5. Indtast formlen for kolonnen (x(i)-x(gennemsnit)). Indtast formlen til beregning af den første subtraktion i celle C2. Denne formel bliver: =A2-___. Udfyld den tomme plads med celleadressen, som indeholder gennemsnittet af x-dataene.

For eksempel beregnes gennemsnittet af de 100 datapunkter i celle A103, så din formel bliver: =A2-A103.

Billede med titlen Beregn kovarians Trin 16

6. Gentag formlen for datapunkterne (y(i)-y(gennemsnit)). Efter samme eksempel vil det være i celle D2. Formlen bliver: =B2-B103.

Billede med titlen Beregn kovarians Trin 17

7. Indtast formlen for kolonnen `Produkt`. I den femte kolonne skal du i celle E2 indtaste formlen for at beregne produktet af de to foregående celler. Dette bliver så: =C2*D2.

Billede med titlen Beregn kovarians Trin 18

8. Kopier formlerne for at udfylde tabellen. Indtil videre har du kun programmeret de første par datapunkter i række 2. Brug din mus til at fremhæve cellerne C2, D2 og E2. Placer din markør på den lille boks i nederste højre hjørne, indtil et plustegn vises. Klik og hold museknappen nede, og træk musen ned for at udvide markeringen og udfylde hele datatabellen. Dette trin kopierer automatisk de tre formler fra cellerne C2, D2 og E2 til hele tabellen. Tabellen skal automatisk udfyldes med alle beregningerne.

Billede med titlen Beregn kovarians Trin 19

9. Programmer summen af den sidste kolonne. Du skal bruge summen af varerne i kolonnen `Produkt`. Indtast formlen i den tomme celle umiddelbart under det sidste datapunkt i den kolonne: =SUM(E2:E___). Udfyld det tomme felt med celleadressen på det sidste datapunkt.

I eksemplet med 100 datapunkter går denne formel ind i celle E103. Type: =SUM(E2:E102).

Billede med titlen Calculate Covariance Step 20

10. Bestem kovariansen. Du kan også lade Excel lave den endelige beregning for dig. Den sidste beregning i celle E103 i vores eksempel repræsenterer tælleren for kovariansformlen. Indtast formlen umiddelbart under den celle: =E103/___. Udfyld det tomme felt med det antal datapunkter, du har. I vores eksempel er dette 100. Resultatet er kovariansen af dine data.

Metode 3 af 4: Brug af online kovariansberegnere

Billede med titlen Calculate Covariance Step 21

1. Søg online efter kovariansberegnere. Forskellige skoler, virksomheder eller andre kilder har hjemmesider, der meget nemt beregner kovariansværdierne for dig. Brug søgeordet `kovariansberegner` i en søgemaskine.

Billede med titlen Beregn kovarians trin 22

2. Indtast dine oplysninger. Læs venligst instruktionerne på hjemmesiden omhyggeligt for at sikre, at du indtaster oplysningerne korrekt. Det er vigtigt, at dine datapar holdes i orden, ellers vil det genererede resultat være en forkert kovarians. Websteder har forskellige dataindtastningsstile.

På hjemmesiden http://ncalculators.com/statistics/covariance-calculator.htm, for eksempel er der en vandret boks til at indtaste x-værdierne og en anden vandret boks til at indtaste y-værdierne. Du skal indtaste dine data adskilt med kommaer. Så x-datasættet beregnet tidligere i denne artikel skal derefter indtastes som 1,3,2,5,8,7,12,2,4. Y-dataene er 8,6,9,4,3,3,2,7,7.

På en anden side, https://www.lommeregneren.co/math/Covariance-Calculator-705.html, du bliver bedt om at indtaste x-dataene i den første boks. Data indtastes lodret med ét element pr. linje. Derfor ser indlægget på denne side således ud:

Billede med titlen Beregn kovarians Trin 23

3. Beregn dine resultater. Det attraktive ved disse online beregninger er, at du efter indtastning af data normalt kun skal klikke på `Beregn`-knappen, hvorefter resultaterne vises automatisk. De fleste websteder vil give dig de mellemliggende beregninger af x(avg), y(avg) og n.

Metode 4 af 4: Fortolkning af resultaterne af kovariansen

Billede med titlen Beregn kovarians Trin 24

1. Se efter et positivt eller negativt forhold. Kovariansen er et enkelt statistisk tal, der angiver forholdet mellem et datasæt og et andet. I eksemplet nævnt i indledningen er højden og vægten målt. Du ville forvente, at når folk vokser, vil deres vægt også stige, hvilket fører til et positivt kovarianssyn. Et andet eksempel: Antag, at der indsamles data, der angiver det antal timer, en person har øvet golf, og den score, han eller hun opnår. I dette tilfælde forventer du en negativ kovarians, hvilket betyder, at når antallet af træningstimer stiger, vil golfresultatet falde. (I golf er en lavere score bedre).

Overvej prøvedatasættet beregnet ovenfor. Den resulterende kovarians er -8,07. Minustegnet betyder, at når x-værdierne stiger, har y-værdierne en tendens til at falde. Du kan se, at dette er sandt ved at se på nogle af værdierne. For eksempel svarer x-værdierne på 1 og 2 til y-værdierne på 7, 8 og 9. X-værdierne på 8 og 12 er knyttet til y-værdierne på henholdsvis 3 og 2 .

Billede med titlen Beregn kovarians trin 25

2. Fortolk størrelsen af kovariansen. Hvis antallet af kovariansscore er stort, enten et stort positivt tal eller et stort negativt tal, så kan du tolke dette som to dataelementer, der er stærkt forbundet, enten på en positiv eller negativ måde.

Kovariansen -8,07 af stikprøvedatasættet er ret stor. Bemærk, at dataene går fra 1 til 12. Så 8 er et ret stort tal. Dette indikerer et ret stærkt forhold mellem datasættene x og y.

Billede med titlen Beregn kovarians Trin 26

3. Forstå manglen på et forhold. Hvis dit resultat er en kovarians lig med eller meget tæt på 0, kan du konkludere, at datapunkterne ikke har nogen sammenhæng. Det vil sige, at en stigning i den ene værdi kan, men behøver ikke at føre til en stigning i den anden. De to udtryk er næsten vilkårligt forbundet.

Antag, at du relaterer skostørrelser til eksamenskarakterer. Fordi der er så mange faktorer, der påvirker en studerendes eksamenskarakterer, kan man forvente en kovariansscore tæt på 0. Dette indikerer, at der næsten ikke er nogen sammenhæng mellem de to værdier.

Billede med titlen Beregn kovarians Trin 27

4. Se forholdet grafisk. For at forstå kovarians visuelt kan du plotte dine datapunkter i en x,y-graf. Når du gør det, bør du ret nemt se, at punkterne, selvom de ikke lige er i en lige linje, har en tendens til at nærme sig en klynge i en diagonal linje fra øverst til venstre til nederst til højre. Dette er beskrivelsen af en negativ kovarians. Du ser også, at værdien af kovariansen er -8,07. Dette er et ret stort antal i forhold til datapunkterne. Det høje tal tyder på, at kovariansen er ret stærk, hvilket kan udledes af datapunkternes lineære form.

For at gennemgå dette igen, læs wikiHow-artikler om tegning af punkter i et koordinatsystem.

Advarsler

Kovarians har begrænset anvendelse i statistik. Det er ofte et skridt i retning af at beregne korrelationskoefficienter eller andre begreber. Vær forsigtig med alt for dristige fortolkninger baseret på en kovariansscore.

Artikler om emnet "Beregn kovarians"

Beregn spearmans rangkorrelationskoefficient

Beregn en rabatprocent

Beregn joule

Beregn volumen og densitet

Оцените, пожалуйста статью