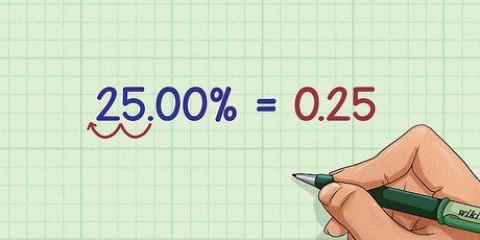Hvis det eksperimentelle mål er 60 cm, så skal beregningen af unøjagtigheden også afrundes til et helt tal. For eksempel kan unøjagtigheden af denne måling være 60 cm ± 2 cm, men ikke 60 cm ± 2.2 cm. Hvis din eksperimentelle læsning er lig med 3.4 cm, så skal unøjagtigheden også afrundes til 0,1 cm. For eksempel kan unøjagtigheden af denne måling være 3.4 cm ± .være 1 cm, men ikke 3.4 cm ± 1 cm. 
Se nøje på kanten af bolden og linealen for at få en idé om, hvor pålidelig din måling kan være. I en standardlineal er 0,5 cm-mærkerne tydeligt markeret - men antag, at du kan komme lidt tættere på end det. Hvis det ser ud til, at du kan komme inden for 0,3 cm med din måling, så er unøjagtigheden 0,3 cm. Nu skal vi måle kuglens diameter. Antag at du får 7,6 cm som svar. Skriv nu den estimerede måling ned med unøjagtigheden. Kuglens diameter er 7,6 cm ± 0,3 cm. 
Antag, at du ikke kan komme meget tættere på end 0,2 cm med en almindelig lineal. Så unøjagtigheden er ± 0,2 cm. Antag, at du målte, at stakken af kasser sammen er 22 cm. Nu skal du bare dividere denne måleværdi og unøjagtigheden med 10 (antallet af felter). 22 cm/10 = 2,2 cm og 0,2 cm/10 = 0,02 cm. Det betyder, at tykkelsen af 1 kasse er lig med 2,20 cm ± 0,02 cm. 



0,43 s – 0,42 s = 0,01 s 0,52s - 0,42s = 0,1s 0,35 s - 0,42 s = -0,07 s 0,29 s - 0,42 s = -0,13 s 0,49 s - 0,42 s = 0,07 s Tilføj nu kvadraterne af forskellene: (0,01 s) + (0,1 s) + (-0,07 s) + (-0,13 s) +(0,07 s)= 0,037 s. Find gennemsnittet af disse tilføjede kvadrater ved at dividere resultatet med 5. 0,037 s/5 = 0,0074 s. 



(10 cm ± .4 cm) - (3 cm ± .2 cm) = (10 cm - 3 cm) ± (.4 cm +. 2 cm) = 7 cm ± 0,6 cm (6 cm ± 0,2 cm) = (0,2 / 6) x 100 og tilføj et %-tegn til det. Det er 3,3 %
Dermed:
(6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3 %) x (4 cm ± 7,5 %) (6 cm x 4 cm) ± (3.3 + 7,5) = 24 cm ± 10,8 % = 24 cm ± 2,6 cm (10 cm ± 0,6 cm) ÷ (5 cm ± 0,2 cm) = (10 cm ± 6%) ÷ (5 cm ± 4%) (10 cm ÷ 5 cm) ± (6 % + 4 %) = 2 cm ± 10 % = 2 cm ± 0,2 cm 
(2,0 cm ± 1.0 cm) = (2,0 cm) ± (1,0 cm) x 3 = 8,0 cm ± 3 cm
Beregn unøjagtighed
Indhold
Når du foretager en måling, mens du indsamler data, kan du antage, at der er en "reel værdi" er inden for rækkevidden af de målinger, du har foretaget. Hvis du vil beregne unøjagtigheden af dine aflæsninger, skal du finde det bedste skøn over din aflæsning og tage højde for det, når du trækker eller adderer unøjagtigheden af aflæsningen.
Trin
Metode 1 af 3: At lære det grundlæggende

1. Bestem den korrekte form for unøjagtighed. Antag, at du måler længden af en pind på omkring 4,2 cm, med en margen på 1 millimeter. Det betyder, at pinden næsten helt sikkert er 4,2 cm, men kan være lidt større eller mindre end denne længde, med en fejlmargin på 1 millimeter.
- Registrer dette som følger: 4,2 cm ± 0,1 cm. Du kan omskrive dette som: 4,2 cm ± 1 mm, fordi 0,1 cm = 1 mm.

2. Afrund den eksperimentelle aflæsning til det samme antal decimaler som unøjagtigheden. Målinger, der involverer unøjagtighed, afrundes normalt til 1 eller 2 signifikante cifre. Nøglepunktet er, at du afrunder eksperimentets målinger til det samme antal decimaler som unøjagtigheden, for at holde målingerne konsistente.

3. Beregn unøjagtigheden af en enkelt måling. Antag, at du måler diameteren på en rund kugle med en lineal. Dette er vanskeligt, fordi det er svært at præcisere, hvor den ydre kant af bolden er, og hvordan man måler den med linealen. Antag, at linealen kan finde diameteren med en nøjagtighed på 0,1 cm - det betyder ikke, at du kan måle kuglens diameter til det præcisionsniveau.

4. Beregn unøjagtigheden af en enkelt måling af flere objekter. Antag, at du måler højden på en stak med 10 cd-hylstre, der alle har dimensioner. Antag, at du vil vide, hvad tykkelsen af 1 kasse er. Denne aflæsning er så lille, at procentdelen af unøjagtighed vil være i overkanten. Men hvis du måler 10 kasser, kan du dividere resultatet og bare dividere dets unøjagtighed med antallet af kasser i stakken for at finde tykkelsen af 1 kasse.

5. Udfør denne måling flere gange. For at øge nøjagtigheden af din måling, uanset om du måler længden af et objekt, eller hvor lang tid det tog at tilbagelægge en bestemt afstand, vil du øge chancerne for en nøjagtig aflæsning, hvis du tager flere målinger. Bestemmelse af gennemsnittet af alle målinger vil i sidste ende resultere i en bedre bestemmelse af unøjagtigheden af en måling.
Metode 2 af 3: Beregning af unøjagtigheden af flere målinger

1. Tag flere målinger. Antag, at du vil beregne, hvor lang tid det tager for en bold at falde fra bordet og ned på runden. For de bedste resultater skal du udføre den samme måling mindst et par gange – lad os sige, at vi gør dette fem gange. Så bliver du nødt til at beregne middelværdien af disse 5 målinger og derefter addere eller trække standardafvigelsen fra denne for det bedste resultat.
- Antag, at du har følgende aflæsninger: 0,43 s, 0,52 s, 0,35 s, 0,29 s og 0,49 s.

2. Bestem gennemsnittet af målingerne. Det gør du ved at lægge dem alle fem sammen og dividere summen med 5, antallet af målte værdier. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2.08 s. Del nu 2.08 gange 5. 2.08/5 = 0,42 sek. Middelværdien er 0,42 s.

3. Bestem variansen af disse målinger. Det gør du ved at bestemme forskellen mellem hver af de 5 målinger og gennemsnittet. Træk aflæsningerne fra 0,42 s. Her er de 5 forskelle:

4. Bestem standardafvigelsen. Dette kan findes ved at beregne kvadratroden af variansen. Kvadratet på 0,0074 s = 0,09 s, så standardafvigelsen er 0,09 s.

5. Angiv den endelige målte værdi. Det gør du ved at notere middelværdien af de målte værdier sammen med den adderede og subtraherede standardafvigelse. Da middelværdien af aflæsningerne er 0,42 s, og standardafvigelsen er 0,09 s, er den endelige aflæsning 0,42 s ± 0,09 s.
Metode 3 af 3: Aritmetiske operationer med unøjagtighed

1. Tilføjelse af unøjagtighed. Du gør dette ved at lægge aflæsningerne sammen og tilføje deres unøjagtigheder:
- (5 cm ± .2 cm) + (3 cm ± .1 cm) =
- (5 cm + 3 cm) ± (.2 cm +. 1 cm) =
- 8 cm ± .3 cm

2. Fratræk unøjagtighed. Det gør du ved at trække de målte værdier fra og tilføje unøjagtighederne:
3. Multiplicer unøjagtighed.
For at gange unøjagtigheden skal du gange målingerne og tilføje den RELATIVE unøjagtighed (som en procentdel):
Beregning af unøjagtigheder gennem multiplikation virker ikke med absolutte værdier (som med addition og subtraktion), men det gør det med relative værdier. Du får den relative unøjagtighed ved at dividere den absolutte unøjagtighed med den målte værdi og derefter gange den med 100.
For eksempel:
For at gange unøjagtigheden skal du gange målingerne og tilføje den RELATIVE unøjagtighed (som en procentdel):
Beregning af unøjagtigheder gennem multiplikation virker ikke med absolutte værdier (som med addition og subtraktion), men det gør det med relative værdier. Du får den relative unøjagtighed ved at dividere den absolutte unøjagtighed med den målte værdi og derefter gange den med 100.
For eksempel:
Dermed:
4. Deler unøjagtighed.
For at opdele unøjagtighed skal du dividere målingerne og tilføje den RELATIVE unøjagtighed:
Denne procedure svarer til en multiplikation!
For at opdele unøjagtighed skal du dividere målingerne og tilføje den RELATIVE unøjagtighed:
Denne procedure svarer til en multiplikation!

5. Øger en unøjagtig læsning eksponentielt. For eksponentielt at øge en unøjagtig måling skal du øge målingen med en bestemt potens og derefter gange unøjagtigheden med denne potens:
Tips
- Du kan se resultater og standardunøjagtigheden som helhed eller for hvert resultat inden for et sæt data. En generel regel er, at data opnået fra flere målinger er mindre nøjagtige end direkte opnået fra en individuel måling.
Advarsler
- Unøjagtighed som beskrevet her gælder kun i de tilfælde, hvor der anvendes normal (gaussisk, klokkeformet) statistik. Andre opslag kræver en anden metode til at beskrive unøjagtighed.
- God forskning slutter aldrig "fakta" eller hvad "rigtigt" er. Selvom en måling med stor sandsynlighed falder inden for et vist område af unøjagtighed, er der ingen garanti for, at den vil. Det er iboende i videnskabelige måleværdier, at der er en mulighed for, at målte værdier er forkerte.
Artikler om emnet "Beregn unøjagtighed"
Оцените, пожалуйста статью
Populær