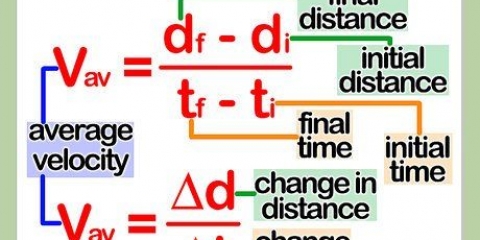
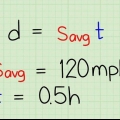Vippens midte=4 meter fra nulpunktet. Barn 1=1 meter væk fra nulpunktet Barn 2=5 meter væk fra nulpunktet 



430 m*kg ÷ 130 kilo=3,31 m Tyngdepunktet er 3,31 meter fra nulpunktet, eller målt fra nulpunktet er det 3,31 meter fra enden af venstre side af vippen, hvor nulpunktet blev placeret. 



Som vi løste det, er nullet på venstre side af vippen. Vores svar er 3,31 m, så vores massecentrum er 3,31 m fra nulpunktet til venstre. Vælger du et nyt nulpunkt, 1 m fra venstre, får du som svar 2,31 m fra massemidtpunktet. Massecentrum er 2,31 m fra det nye nulpunkt, altså 1 m fra venstre. Massecentrum er 2,31 + 1=3,31 m fra venstre, og derfor samme svar som vi beregnede før. (Bemærk: Når du måler afstand, så husk at afstande venstre fra nulpunktet er negative, og afstande ret af det positivt.) 
I vippeproblemer er det eneste, der betyder noget, hvor tyngdepunktet er fra venstre mod højre langs vippens linje. Senere kan du lære mere avancerede måder at beregne tyngdepunktet i to dimensioner på.
Beregn tyngdepunktet
Indhold
Tyngdepunktet (massecentret) er centrum for et objekts vægtfordeling - det punkt, hvor tyngdekraften virker på det objekt. Dette er det punkt, hvor objektet er i perfekt balance, uanset hvordan objektet er snoet eller roteret omkring det punkt. Hvis du vil vide, hvordan man beregner et objekts tyngdepunkt, har du brug for vægten af objektet og af alle objekterne på det. Derefter bestemmer du et nul, og du behandler de kendte størrelser i ligningen for at beregne tyngdepunktet for et objekt eller system. Hvis du vil vide, hvordan du beregner tyngdepunktet, skal du følge nedenstående trin.
Trin
Metode 1 af 4: Bestem vægten

1. Beregn vægten af objektet. Når du beregner tyngdepunktet, skal du først finde ud af objektets vægt. Lad os sige, at du vil beregne vægten af en vippe med en masse på 30 kilo. Da det er et symmetrisk objekt, vil dets tyngdepunkt være nøjagtigt i midten (hvis ingen sidder på det). Men hvis der er folk med forskellig masse på vippen, så bliver problemet lidt mere kompliceret.

2. Beregn de ekstra vægte. For at bestemme tyngdepunktet for vippen med to børn på, skal du bestemme den individuelle vægt af hvert barn. Det første barn vejer 40 kilo og det andet barn vejer 60 kilo.
Metode 2 af 4: Bestem nulpunktet

1. Vælg et nulpunkt. Nulpunktet er ethvert startpunkt på den ene side af vippen. Du kan placere nullet på den ene side af vippen eller på den anden side. Lad os sige, at vippen er 6 meter lang. Lad os sætte nullet på venstre side af vippen, tæt på det første barn.

2. Mål afstanden fra nulpunktet til midten af hovedobjektet samt til de to ekstra vægte. Lad os sige, at børnene er hver 1 meter fra hver ende af vippen. Vippens centrum er midten af vippen, eller 3 meter, fordi 6 meter divideret med 2 er lig med 3. Her er afstandene fra midten af det største objekt, og de to ekstra vægte danner nulpunktet:
Metode 3 af 4: Bestem tyngdepunktet

1. Multiplicer afstanden af hvert objekt til nulpunktet med dets vægt for at finde øjeblikket. Dette giver dig tidspunktet for hvert objekt. Sådan ganges afstanden mellem hvert objekt fra nulpunktet med dets vægt:
- Vippen: 30 kilo x 3 m=90 m*kg.
- Barn 1=40 kilo x 1 m=40 m*kg.
- Barn 2=60 kilo x 5 m=300 m*kg.

2. Læg de tre øjeblikke sammen. Beregn blot følgende: 90 m*kg + 40 m*kg + 300 m*kg=430 m*kg. Det samlede moment er 430 m*kg.

3. Læg vægten af alle genstande sammen. Find summen af vippens vægt og de to børn. Gør dette på følgende måde: 30 kilo + 40 kilo + 60 kilo = 130 kilo.

4. Divider det samlede moment med den samlede vægt. Henter afstanden fra nulpunktet til objektets tyngdepunkt. Dette ved at dividere 430 m * kg med 130 kilo.
Metode 4 af 4: Tjek dit svar

1. Find tyngdepunktet i diagrammet. Hvis det tyngdepunkt, du har fundet, er uden for objektsystemet, så har du fundet det forkerte svar. Måske har du beregnet afstanden fra mere end ét punkt. Prøv igen med kun ét nulpunkt.
- For personer, der f.eks. sidder på vippen, skal tyngdepunktet være et sted på vippen, ikke til venstre eller højre for vippen. Det behøver ikke at være på en person.
- Det gælder også problemer i to dimensioner. Tegn en firkant lige stor nok til at passe til alle objekterne i dit problem. Tyngdepunktet skal være inden for denne firkant.

2. Tjek dine beregninger, hvis dit svar er for lille. Hvis du vælger den ene ende af systemet som dit nul, så placerer et lille svar tyngdepunktet lige ved siden af den ene ende. Dette kan være det rigtige svar, men det er ofte en indikation af, at noget er gået galt. Har I vægten og afstanden med hinanden i regnestykket ganget? Det er den rigtige måde at finde dette øjeblik på. Hvis du ved et uheld lagt sammen, så får du nok et meget mindre svar.

3. Tjek din udregning, hvis du har fundet mere end ét tyngdepunkt. Hvert system har kun et enkelt tyngdepunkt. Hvis der er flere, har du måske sprunget over det trin, hvor du skulle lægge alle øjeblikke sammen. Tyngdepunktet er det i alt moment divideret med i alt vægt. Du behøver ikke at hver øjeblik at dele med hver vægt, som kun giver dig placeringen af hvert objekt.

4. Markér nul, hvis dit svar er et heltal fra. Svaret i vores eksempel er 3,31 m Antag, at du fik 2,31 m, 4,31 m eller et andet tal, der ender på `.31.Dette skyldes sandsynligvis, at vi valgte den venstre ende af vippen som nul, mens du valgte den højre ende eller et andet punkt en heltal afstand fra vores nul. Dit svar er korrekt, uanset hvilket nul du vælger! Det skal du bare huske nullet står altid for x=0. Her er et eksempel:

5. Sørg for, at alle dine mål er lige linjer. Antag at du ser et andet eksempel med "børn på vippen", men det ene barn er meget større end det andet, eller en dreng hænger under vippen i stedet for at sidde på den. Ignorer forskellen og tag alle dine mål langs vippens lige linje. Måling af afstande i en vinkel vil give svar, der er tæt på, men lidt anderledes.
Tips
- For at bestemme afstanden en person skal bevæge sig for at balancere vippen på støtten, skal du bruge denne formel: (flytter vægten) / (totalvægt)=(afstand som tyngdepunktet har bevæget sig over) / (afstand, som vægten er blevet flyttet over). Denne formel kan omskrives for at vise, at afstanden, som vægten (personen) skal flyttes, er lig med afstanden mellem tyngdepunktet og omdrejningspunktet, gange personens vægt divideret med den samlede vægt. Det skal det første barn også -1,31 m *40 kilo / 130 kilo=-0.flyt 40 m (til enden af vippen). Eller skal det andet barn -1.08 m *130 kilo / 60 kilo=-2.bevæge sig 84 m. (til midten af vippen).
- For at finde tyngdepunktet for et todimensionelt objekt skal du bruge formlen Xcg=∑xW/∑W til at finde tyngdepunktet langs x-aksen, og Ycg=∑yW/∑W for at finde tyngdepunktet langs y-aksen. Det punkt, hvor de skærer hinanden, er tyngdepunktet.
- Definitionen af tyngdepunktet for en generel massefordeling er (∫ r dW/∫ dW), hvor dW er lig med den afledede af vægten, r er positionsvektoren, og hvor integralerne skal fortolkes som Stieltjes-integraler over helheden legeme. De kan dog udtrykkes som mere konventionelle Riemann- eller Lebesgue-volumenintegraler for fordelinger med en sandsynlighedstæthedsfunktion. Startende med denne definition kan alle egenskaber af tyngdepunktet, inklusive dem, der bruges i denne artikel, udledes af egenskaberne for Stieltjes-integraler.
Advarsler
- Forsøg ikke blindt at anvende disse mekanikker uden at forstå teorien, hvilket kan føre til fejl. Prøv først at forstå de underliggende love/teorier.
Artikler om emnet "Beregn tyngdepunktet"
Оцените, пожалуйста статью
Populær