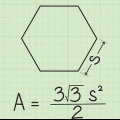
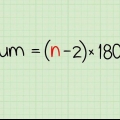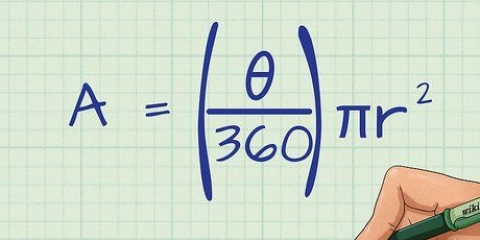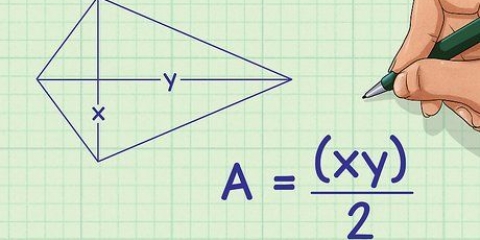Vinklerne i en trekant (en 3-sidet polygon) er i alt 180 grader. Vinklerne i en firkant (en 4-sidet polygon) er i alt 360 grader. Vinklerne i en femkant (en 5-sidet polygon) er i alt 540 grader. Vinklerne i en sekskant (en 6-sidet polygon) er i alt 720 grader. Vinklerne i en ottekant (en 8-sidet polygon) er i alt 1080 grader. 
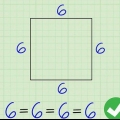
Hvis polygonen er en regulær polygon, skal du bare dividere summen af alle vinkler med antallet af vinkler. Enhver vinkel i en ligesidet trekant er således 180/3=60 grader, og enhver vinkel på et kvadrat er 360/4=90 grader. (Selvom et rektangel per definition ikke er en regulær polygon, er alle vinkler også rette vinkler og derfor 90 grader). Hvis en polygon ikke er en regulær polygon, skal du kende størrelsen af de andre vinkler for at beregne størrelsen af den ukendte vinkel. gå til næste trin. 
Hvis to af vinklerne i en trekant er 60 og 80 grader, skal du lægge disse vinkler sammen (60 + 80=140). Træk derefter denne sum fra summen af vinklerne i en trekant, 180 grader: 180-140=40 grader. (En sådan trekant, hvor alle vinkler er forskellige, kaldes en skala-trekant). Du kan skrive ovenstående metode som en formel: -en=180 – (b + c), hvorved -en er den vinkel du vil bestemme, og b og c de vinkler, der er kendt. For polygoner med mere end 3 sider skal du erstatte `180` med summen af vinklerne som specifikke for den polygon og tilføje et andet udtryk for hver yderligere kendt vinkel. For nogle polygoner er en `hurtigere løsning` mulig til at bestemme den ukendte vinkel. En ligebenet trekant er en trekant med to lige lange sider og to vinkler af samme størrelse. Et parallelogram er en firkant med modsatte sider af samme længde og diagonalt modsatte vinkler af samme størrelse. 

Hvis du kender længden af den modsatte side (i forhold til vinklen) og længden af hypotenusen (siden modsat den rette vinkel), skal du bruge sinusfunktionen (længden af den modsatte side divideret med længden af hypotenusen). silke). Hvis du kender længden af den tilstødende rektangulære side og længden af hypotenusen, kan du bruge cosinusfunktionen (længden af den tilstødende side divideret med længden af hypotenusen). Hvis du kender længderne af de modstående sider og tilstødende sider, kan du bruge tangentfunktionen (længden af den modsatte side divideret med længden af den tilstødende side). 
At dividere den modsatte værdi 5 med hypotenusen (hypotenusen) 10 giver brøken 5 / 10=0,5. 
I dagene før lommeregnere bør du konsultere en trykt tabel med værdier for sinus, cosinus og tangens af vinkler fra 0 til 90 grader. Følg sinuskolonnen, indtil du finder værdien `0,5` og find derefter den vinkel, der svarer til denne sinusværdi. Hvis du har en lommeregner med trigonometriske funktioner, kan du indtaste sinus som værdien (hvis du ikke allerede har brugt lommeregneren til at dividere den modsatte side med hypotenusen for at finde denne værdi) og derefter trykke på den eller de relevante taster. Afhængigt af lommeregnerens mærke skal du trykke på en enkelt tast mærket `sin` eller en tast mærket `Inv`, `2ndF` eller `Shift`, før du trykker på `sin`-tasten. Uanset hvilken metode du bruger til at løse dette eksempel, skal du i alle tilfælde finde en vinkel på 30 grader.
Beregn vinkler
Indhold
I geometri er en vinkel rummet mellem to stråler eller linjestykker, der har samme endepunkt eller toppunkt. Den mest almindelige måde at måle vinkler på er i grader, hvor en fuld cirkel er 360 grader. Du kan beregne vinklen i en polygon, hvis du kender formen på polygonen og størrelsen af de andre vinkler, eller i tilfælde af en retvinklet trekant, hvis du kender størrelsen af de to sider.
Trin
Metode 1 af 2: Beregning af vinklen i en polygon

1. Tæl antallet af sider af polygonen.

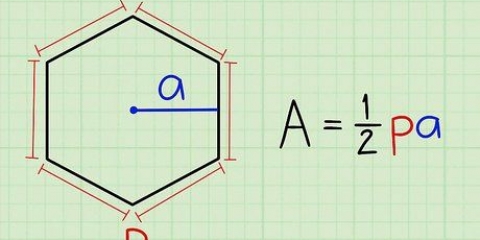
2. Find summen af alle vinkler i polygonen. Formlen til at finde det samlede mål for alle indvendige vinkler i en polygon er (n – 2) x 180, hvor n er antallet af sider, samt antallet af vinkler af polygonen. Nogle almindelige totaler af vinklerne i en polygon er:

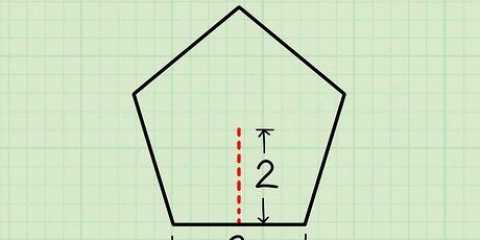
3. Bestem om polygonen er en regulær polygon. En regulær polygon er en polygon med alle sider lige lange og alle vinkler lige store. Ligesidede trekanter og firkanter er eksempler på regulære polygoner, mens Pentagon i Washington DC er et eksempel på en regulær femkant, og et stopskilt er et eksempel på en regulær ottekant.

4. Læg polygonens kendte vinkler sammen, og subtraher summen fra summen af alle vinkelmål for polygonen. De fleste lignende geometriproblemer fungerer med trekanter eller firkanter, fordi der er færre tal at behandle, og så vil vi.
Metode 2 af 2: Beregn vinklen i en retvinklet trekant

1. Find ud af, hvad du allerede ved. En retvinklet trekant kaldes så, fordi en af dens vinkler er en ret vinkel. Du kan bestemme de andre vinkler, hvis du kender nogen af følgende:
- Størrelsen af den tredje vinkel. I dette tilfælde kan du lægge størrelsen af vinklen til 90, antallet af grader af den rette vinkel, og derefter trække totalen fra 180.
- Størrelsen af to sider af trekanten. I dette tilfælde kan du bestemme størrelsen af vinklen ved hjælp af trigonometri.

2. Bestem hvilken trigonometrisk funktion der skal bruges. Trigonometriske funktioner er forhold mellem to af de tre sider af en trekant. Selvom der er seks trigonometriske funktioner, er følgende tre oftest brugt:

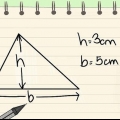
3. Find forholdet mellem de to kendte sider. Antag i dette eksempel, at siden modsat vinklen har en længde på 5 og hypotenusen har en længde på 10. Da modsætningen og hypotenusen således er givet, er forholdet, vi her har at gøre med, det for sinus.

4. Find den vinkel, der svarer til forholdet mellem den trigonometriske funktion. Da vi bruger sinus til at finde vinklen, kaldes den vinkel, vi leder efter, arcsinus eller invers sinus. Der er to måder at finde det på:
Tips
- Vinkler refereres til ved antallet af grader, de måler. Som nævnt ovenfor har en ret vinkel 90 grader. En vinkel større end 0 men mindre end 90 grader er en spids vinkel. En vinkel større end 90 men mindre end 180 grader er en stump vinkel. En vinkel på 180 grader er en ret vinkel, mens en vinkel større end 180 grader er en tilbagevendende vinkel.
- To vinkler med i alt 90 grader kaldes komplementære vinkler (de to andre vinkler end den rette vinkel i en retvinklet trekant er komplementære vinkler). To vinkler, hvis vinkler summeres til 180 grader, kaldes supplerende vinkler.
Fornødenheder
- Trigonometriske tabeller eller en lommeregner med trigonometriske funktioner
Artikler om emnet "Beregn vinkler"
Оцените, пожалуйста статью
Populær