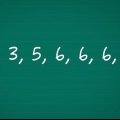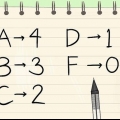Sådan beregnes Spearmans rangkorrelationskoefficient

Indhold

Trin
Tips
Advarsler

Med Spearmans rangkorrelationskoefficient kan du se, om to variable er relateret af en monoton funktion (d.w.z. at hvis et tal stiger, stiger det andet tal også eller omvendt). For at beregne Spearmans rangkorrelationskoefficient skal du bestille og sammenligne datasæt for at finde Σd og derefter indtaste denne værdi i standard- eller forenklet version af Spearmans rangkorrelationskoefficientformel. Du kan også beregne denne koefficient med Excel-formler eller R-kommandoer.

Trin

Metode 1 af 3: Manuelt

1. Tegn din datatabel. Organiserer den information, du har brug for til at beregne Spearmans rangkorrelationskoefficient. Du mangler:

6 kolonner med overskrifter, som vist ovenfor.
Så mange rækker, som du har datapar.

2. Udfyld de to første kolonner med dine datapar.

3. Arranger datapunkterne i den første kolonne i den tredje kolonne, fra 1 til n (det samlede antal datapunkter, du har). Giv det laveste nummer position 1, det næste nummer position 2, og så videre.

4. Gør det samme med den fjerde kolonne som i trin 3, men arranger nu den anden kolonne.

Hvis du har to (eller flere) datapunkter med samme værdi i en kolonne, skal du tage gennemsnittet af de positioner, som disse datapunkter normalt ville have, og give datapunkterne dette gennemsnit som deres nye position.
I eksemplet til højre er der to femmere, der normalt ville være i position 2 og 3. Det er to ens sange, altså tage gennemsnittet af deres stillinger. Middelværdien af 2 og 3 er 2,5, så giv begge femmere position 2,5.

5. I kolonnen `d` beregnes forskellen mellem de to positioner i hvert datapar. Med andre ord, hvis den ene har position 1 og den anden har position 3, er forskellen 2. (Positivt eller negativt er ligegyldigt, da vi vil udligne denne forskel i næste trin.)

6. Kvadret værdierne i d-kolonnen, og skriv disse værdier i d-kolonnen.

7. Læg alle datapunkter i d-kolonnen sammen. Denne værdi er Σd.

8. Vælg en af formlerne nedenfor:

Hvis der ikke forekom ens datapunkter i de foregående trin, indtast Σd i den simple formel for Spearmans rangkorrelationskoefficient

og indtast antallet af datapar for `n` for at finde dit svar.

Hvis lignende datapunkter fandt sted i de foregående trin, skal du bruge standardformlen for Spearmans rangkorrelationskoefficient:

9. Fortolk resultatet. Dette kan variere mellem -1 og 1.

Tæt på -1 – Negativ korrelation.

Tæt på 0 – Ingen lineær korrelation.

Tæt på 1 – Positiv korrelation.

Metode 2 af 3: I Excel

1. Opret nye kolonner med positionerne for de eksisterende kolonner. For eksempel, hvis du har dine data i kolonne A2:A11, vil du bruge formlen `=RANK(A2,A$2:A$11)` og udvide intervallet på tværs af alle dine rækker og kolonner.

2. Behandl lige datapunkter som beskrevet i trin 3 og 4 i metode 1.

3. I en ny celle skal du lave en korrelationsberegning mellem de to kolonner med en formel som `=CORREL(C2:C11,D2:D11)`. I dette tilfælde er C og D positionskolonnerne. Spearmans rangkorrelationskoefficient vises i korrelationscellen.

Metode 3 af 3: Med R

1. Installer R, hvis du ikke allerede har det. (Se https://www.r-projekt.org/.)

2. Gem dine data som en CSV-fil med de data, du ønsker at korrelere i de første to kolonner. Du kan gøre dette med menuen `Gem som`.

3. Åbn R-editoren. Hvis du arbejder i terminalen, skal du blot køre R. Når du er på dit skrivebord, skal du klikke på R-logoet.

4. Indtast følgende kommandoer:

d <- Læs.csv("NAME_OF_YOU_CSV.csv") og tryk på enter

cor(rang(d[,1]),rang(d[,2]))

Tips

For de fleste datasæt har du brug for mindst fem datapar for at etablere en tendens (kun tre par blev brugt i eksemplet for at gøre eksemplet lettere).

Advarsler

Spearmans rangkorrelationskoefficient viser kun korrelationsstyrke, hvis datapunkterne konstant stiger eller falder. Hvis spredningsdiagrammet af datapunkterne viser en anden tendens, vil Spearmans rangkorrelationskoefficient øge korrelationen ikke vises korrekt.
Denne formel er baseret på den antagelse, at der ikke er ens datapunkter. Hvis der er ens datapunkter, som i eksemplet ovenfor, skal du bruge følgende definition: produkt-moment-korrelationskoefficienten for rækkerne.