Sådan beregnes standardafvigelse

Indhold

Trin

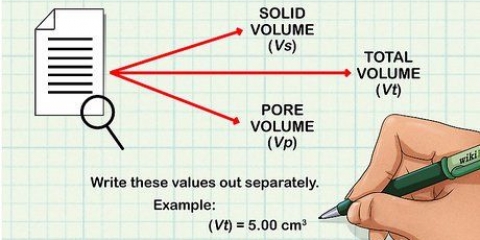
Standardafvigelsen fortæller dig, hvad spredningen af tallene i din prøve er. For at finde standardafvigelsen for dit stikprøve eller datasæt, skal du først lave nogle beregninger. Du skal bestemme gennemsnittet og variansen af dine data, før du kan beregne standardafvigelsen. Variansen er et mål for spredningen af dine værdier omkring middelværdien. Standardafvigelsen bestemmes ved at beregne kvadratroden af variansen.Denne artikel fortæller dig, hvordan du beregner middelværdi, varians og standardafvigelse.

Trin

Metode 1 af 3: Beregn gennemsnittet

1. Se på din dataindsamling. Dette er et vigtigt trin i enhver statistisk beregning, selv en simpel værdi såsom middelværdi eller median.

Ved, hvor mange tal din prøve indeholder.
Ligger tallene langt fra hinanden?? Eller er forskellene mellem tallene små, for eksempel kun få decimaler?
Ved, hvilken type data du kigger på. Hvad betyder tallene i din prøve? Det kan for eksempel være testkarakterer, pulsværdier, højde, vægt og så videre.
For eksempel består et testkarakterdatasæt af tallene 10, 8, 10, 8, 8 og 4.

Billede med titlen Beregn standardafvigelse Trin 2

2. Saml alle dine data. Du skal bruge hvert tal i din prøve for at beregne middelværdien.

Middelværdien er middelværdien af alle tal.

Du beregner middelværdien ved at lægge alle tallene i din prøve sammen og derefter dividere denne værdi med antallet af tal i din prøve (n).

Testkarakterdatasættet (10, 8, 10, 8, 8 og 4) består af 6 numre. Derfor gælder: n = 6.

Billede med titlen Beregn standardafvigelse Trin 3

3. Læg tallene i din prøve sammen. Dette er det første trin i beregningen af det aritmetiske middel eller middelværdi.

Brug f.eks. testkarakterdatasættet: 10, 8, 10, 8, 8 og 4.

10 + 8 + 10 + 8 + 8 + 4 = 48. Dette er summen af alle tal i datasættet eller stikprøven.

Tilføj tallene endnu en gang for at kontrollere svaret.

Billede med titlen Beregn standardafvigelse Trin 4

4. Divider summen med antallet af tal i din prøve (n). Beregner gennemsnittet af alle data.

Testkarakterdatasættet (10, 8, 10, 8, 8 og 4) består af seks tal. Derfor gælder: n = 6.

Summen af alle prøvekaraktererne i eksemplet var 48. Så du skal dividere 48 med n for at beregne middelværdien.

48/6 = 8

Den gennemsnitlige prøvekarakter i stikprøven er 8.

Metode 2 af 3: Find variansen i din prøve

Billede med titlen Beregn standardafvigelse Trin 5

1. Bestem variansen. Variansen er et tal, der angiver spredningen af dine værdier omkring middelværdien.

Dette tal vil give dig en idé om, hvor meget værdierne adskiller sig fra hinanden.
Prøver med lav varians indeholder værdier, der afviger lidt fra gennemsnittet.
Prøver med høj varians indeholder værdier, der afviger meget fra middelværdien.
Variansen bruges ofte til at sammenligne spredningen af værdier i to datasæt.

Billede med titlen Beregn standardafvigelse Trin 6

2. Træk gennemsnittet af hvert af tallene i din prøve fra. Du får nu en række værdier, der angiver, hvor meget hvert tal i prøven afviger fra gennemsnittet.

I vores stikprøve af testkarakterer (10, 8, 10, 8, 8 og 4) var gennemsnittet eller det aritmetiske gennemsnit 8.

10-8 = 2; 8 - 8 = 0,10 - 8 = 2,8 - 8 = 0,8 - 8 = 0 og 4 - 8 = -4.

Gentag beregningerne igen for at kontrollere hvert svar. Det er meget vigtigt, at alle tal er korrekte, fordi du skal bruge dem til næste trin.

Billede med titlen Beregn standardafvigelse Trin 7

3. Kvadret alle de tal, du beregnede i det foregående trin. Du har brug for alle disse værdier for at bestemme variansen af din prøve.

Husk, hvordan vi i vores prøve trak middelværdien (8) fra hvert af tallene i prøven (10, 8, 10, 8, 8 og 4), og vi fik følgende resultater: 2, 0, 2, 0 , 0 og -4.

I den følgende beregning for at bestemme variansen skal du gøre følgende: 2, 0, 2, 0, 0 og (-4) = 4, 0, 4, 0, 0 og 16.

Tjek venligst dine svar, før du går videre til næste trin.

Billede med titlen Beregn standardafvigelse Trin 8

4. Læg de kvadrerede tal sammen. Dette er summen af kvadraterne.

I vores prøvekaraktereksempel beregnede vi følgende kvadrater: 4, 0, 4, 0, 0 og 16.

Husk, at vi i eksemplet startede med testkarakterer ved at trække gennemsnittet af hvert af tallene fra og derefter kvadrere resultaterne: (10-8) + (8-8) + (10-2) + (8- 8) + ( 8-8) + (4-8)

4 + 0 + 4 + 0 + 0 + 16 = 24.

Summen af kvadraterne er 24.

Billede med titlen Beregn standardafvigelse Trin 9

5. Divider summen af kvadrater med (n-1). Husk, at n repræsenterer antallet af tal i prøven. Ved at udføre dette trin bestemmer du variansen.

Vores prøve af testkarakterer (10, 8, 10, 8, 8 og 4) består af 6 cifre. Derfor gælder: n = 6.

n - 1 = 5.

Summen af kvadrater for denne prøve var 24.

24/5 = 4,8.

Så variansen af denne prøve er 4,8.

Metode 3 af 3: Beregning af standardafvigelsen

Billede med titlen Beregn standardafvigelse Trin 10

1. Bemærk afvigelsen. Du skal bruge denne værdi for at beregne standardafvigelsen for din prøve.

Husk, at variansen er, hvor meget værdierne afviger fra middelværdien.
Standardafvigelsen er en lignende værdi, der angiver spredningen af tallene i din prøve.
I vores testkaraktereksempel var variansen 4,8.