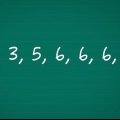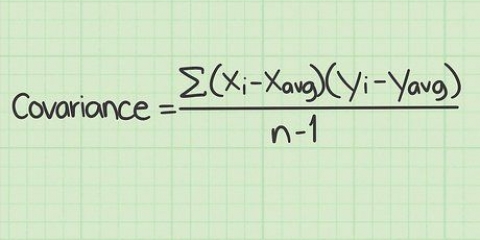Beregning af varians: 8 trin (med billeder)

Indhold

Trin
Tips

Ved at beregne variansen kan du måle spredningen af et sæt værdier - i hvilken grad et antal værdier adskiller sig fra hinanden. Varians er en af komponenterne i sandsynlighedsfordelingen og angiver i hvilket omfang værdier afviger fra middelværdien. Varians bruges ofte sammen med standardafvigelsen (kvadratroden af variansen). Hvis du vil vide, hvordan man beregner variansen af et sæt værdier, skal du følge nedenstående trin.

Trin

1. Skriv formlen til beregning af variansen. Estimatet til beregning af et tilfældigt estimat af populationsvariansen fra en fast stikprøve af n observationer er følgende definition:(s) = Σ [(x_jeg - x̅)]/n - 1. Formlen til beregning af variansen i en hel population er den samme som den foregående, bortset fra at nævneren ikke er lig med n – 1, men med n. Så længe du har at gøre med et begrænset sæt observationer, er det bedre at bruge den første formel. Her er en forklaring af formlens variabler:

s = Varians
Σ = Summation, summen af alle led i ligningen efter summeringstegnet.
x_jeg = Prøveværdierne.
x̅ = Middelværdien af værdierne i serien.
n = Prøvestørrelsen. Antallet af værdier i serien.

2. Beregn summen af værdierne i serien. Opret først en tabel med en kolonne for værdierne, værdien minus middelværdien (x_jeg - x̅) og derefter kvadratet af disse led [(x_jeg - X))]. Når du er færdig med tabellen og udfyldt den første kolonne, skal du sammenlægge alle værdierne i serien. Antag, at du har at gøre med følgende talrække: 17, 15, 23, 7, 9, 13. Dette er lagt sammen: 17 + 15 + 23 + 7 + 9 + 13 = 84.

3. Beregn gennemsnittet. Divider summen af tallene i serien med antallet af elementer i serien for at beregne middelværdien. Så i dette tilfælde summen 84 divideret med antallet af tal, 6. 84/6 = 14. skrive "14" helt nederst i kolonnen som gennemsnit.

4. Træk middelværdien af hver værdi af serien fra. Træk 14 fra hver værdi i serien og udfyld den tredje kolonne (prøvegennemsnittet). Du kan tjekke dit arbejde ved at kontrollere, om summen af alle resultater er nul. Sådan beregnes afvigelsen fra middelværdien for hver værdi i serien:

17 - 14 = 3

15 - 14 = 1

23 - 14 = 9

7 - 14 = -7

9 - 14 = -5

13 - 14 = -1

5. Kvadret hvert resultat. Efter at have beregnet afvigelsen fra middelværdien skal du kvadrere den og skrive svaret i fjerde kolonne. Så alle svar er positive. Sådan fungerede det:

3 = 9

1 = 1

9 = 81

(-7)= 49

(-5) = 25

(-1)= 1

6. Beregn summen af kvadrater. Læg resultaterne sammen. 9 + 1 + 81 + 49 + 25 + 1 = 166

7. Erstat værdierne i ligningen. Udfyld værdierne i ligningen. Huske på, at "n" repræsenterer antallet af elementer i sekvensen.

s = 166/(6-1)

8. Løse. Divider nu 166 med 5. Resultatet er 33,2. Hvis du også vil kende standardafvigelsen, så find kvadratroden af 33,2. √33,2 = 5,76. Nu kan du begynde at fortolke disse data i forhold til det store billede. Normalt sammenlignes variansen af to serier. Den laveste værdi betyder, at variansen i den serie er mindre stor.