Beregning af volumen og tæthed: 11 trin (med billeder)

Indhold

Trin
Tips
Advarsler

Volumen er mængden af plads et objekt optager, mens tæthed er objektets masse pr. volumenenhed. Du skal først kende rumfanget af et objekt, før du kan beregne dens massefylde. Du kan beregne volumen for almindelige objekter med en simpel formel, bestemt af objektets form. Almindeligt anvendte enheder for volumen er kubikcentimeter (cm) og kubikmeter (m). Når du har beregnet volumen, så bestemmes massefylden med en simpel udregning. Almindeligt anvendte enheder for massefylde er gram per kubikcentimeter (g/cm) eller gram per milliliter (g/mL).

Trin

Del 1 af 3: Beregning af volumen af et regulært objekt

Billede med titlen Calculate Volume and Density Step 1.jpg

1. Bestem formen på objektet. Ved at kende formen på et objekt kan du bestemme den korrekte formel og lave de nødvendige beregninger for volumenet.

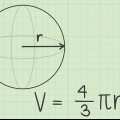
EN kugle er et perfekt rundt tredimensionelt objekt, hvor hvert punkt på dets overflade er lige langt fra midten. Med andre ord er en kugle et sfærisk objekt.
EN kegle er et tredimensionelt objekt med en cirkulær base og et punkt. En anden måde at tænke på dette er, at en kegle er en speciel slags pyramide med en cirkulær base.
EN terning er en tredimensionel form med seks identiske firkantede flader.
EN parallelepipedum, også kaldet et rektangulært prisme, ligner en terning, da det er en tredimensionel form med seks sider, men i dette tilfælde er siderne rektangulære i stedet for kvadratiske.
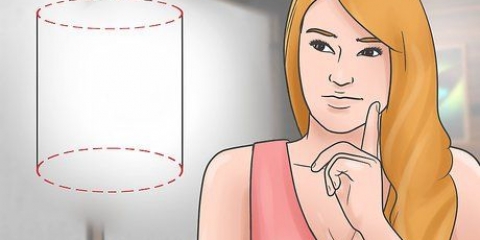
EN cylinder er en tredimensionel form med to identiske flade cirkler og en enkelt buet flad overflade, der forbinder begge cirkler.
EN pyramide er en tredimensionel form med en polygon som sin base og skrå sider, der mødes i et punkt (pyramidens spids).En regulær pyramide er en pyramide med en regulær polygon som bunden af pyramiden, hvilket betyder, at alle sider af polygonen er lige lange, og alle vinkler er lige store.
Hvis dit objekt har en uregelmæssig form, kan du bruge forskydningsmetoden til at bestemme dets volumen.

Billede med titlen Calculate Volume and Density Step 2b.jpg

2. Vælg den korrekte ligning til beregning af volumen. Hver form har sin egen formel til at beregne, hvor meget tredimensionel plads den fylder. Nedenfor finder du formlerne for de tidligere nævnte objekter. Læs mere om det beregne volumen for mere detaljerede eksempler og billeder af disse formler.

bol:

V = \frac{4}{3} π r^{3},

$V={frac{4}{3}}pi r^{{3}},$ hvor r er kuglens radius.

Kegle:

V = \frac{1}{3} π r^{2} h,

$V={frac{1}{3}}pi r^{{2}}h,$ hvor r er radius af den cirkulære base og h er højden af keglen.

terning:

V = s 3,

$V=s^{{3}},$ hvor s er længden af en side.

Rektangulær prisme:

V = l w h,

$V=lwh,$ hvor l er længden af en side af en rektangulær flade, w er bredden af en rektangulær flade og h er højden af prismet.

Cylinder:

π r 2 h,

$pi r^{{2}}h,$ hvor r er radius af den cirkulære base og h er højden af keglen.

Pyramide:

V = \frac{1}{3} B h,

$V={frac{1}{3}}Bra,$ hvor B er arealet af bunden af pyramiden og h er højden af pyramiden.

Billede med titlen Calculate Volume and Density Step 3.jpg

3. Foretag de nødvendige målinger. De mål, du skal bruge, bestemmes af genstandens form. For de fleste objekter har du brug for højden, men radius er nok, hvis formen er cirkulær, eller længden og bredden af objekter med rektangulære flader.

Radius af en cirkel er halvdelen af dens diameter. Mål diameteren med en lineal gennem midten af cirklen og aflæs aflæsningen. Beregn radius ved at dividere diameteren med to.

At bestemme radius af en kugle kræver lidt mere indsats, men kan gøres på flere måder, som vist i denne artikel.

Længden, bredden og højden af objekter kan måles med en lineal, der måler fra den ene ende af et objekt til den anden.

Billede med titlen Calculate Volume and Density Step 4b.jpg

4. Beregn volumen. Nu hvor du har bestemt formen, ved hvilken formel du skal bruge og har taget de nødvendige mål, kan du beregne volumen. Indtast dine aflæsninger og udfør de nødvendige beregninger. Det endelige produkt er volumen af dit objekt.

Glem ikke at give dit svar i kubikenheder. Uanset om du bruger metrikker eller SI`er, er volumenenheden altid kubisk. Tilføj altid enheder i slutningen af din beregning.

Del 2 af 3: Beregn rumfanget af et uregelmæssigt objekt

Billede med titlen Calculate Volume and Density Step 5.jpg

1. Beregn volumen af objektet ved hjælp af forskydning. Det kan være svært at bestemme dimensionerne af uregelmæssigt formede genstande, hvilket efterfølgende vil føre til forkerte mål og volumenberegninger. Ved at måle, hvor meget vand der fortrænges af et objekt, kan du beregne dets volumen uden komplekse formler.

Denne metode kan også bruges til at beregne volumenet af en regulær form.

Billede med titlen Calculate Volume and Density Step 6.jpg

2. Fyld en målecylinder med vand. En gradueret cylinder er et laboratorieinstrument med markeringer på ydersiden og giver dig mulighed for at måle volumen af en vis mængde væske. Sørg for, at den graduerede cylinder er stor nok til at holde genstanden. Fyld den med nok vand, så genstanden er helt nedsænket, men vandet løber ikke ud over kanten. Bemærk det oprindelige niveau af vandet.

Når du måler den oprindelige mængde vand, skal du se på væskeniveauet i øjenhøjde og notere aflæsningen på undersiden af menisken. Menisken er den kurve, som vand laver, når det kommer i kontakt med en overflade.

Billede med titlen Calculate Volume and Density Step 7.jpg

3. Læg genstanden roligt i koppen. Pas på ikke at tabe genstanden i vandet, da der ellers kan strømme vand ud over kanten, og aflæsningen bliver forkert. Sørg for, at genstanden er helt nedsænket i vand. Bemærk den nye vandstand i koppen, igen i øjenhøjde, og vær meget opmærksom på menisken.

Hvis du spildte vand, mens du placerede genstanden i koppen, prøv igen med en større målekop, eller brug mindre vand.

Billede med titlen Calculate Volume and Density Step 8.jpg

4. Træk det nye vandniveau fra det oprindelige niveau. Mængden af vand, der fortrænges af objektet, er lig med objektets volumen målt i kubikcentimeter. Væsker måles normalt i milliliter, og en milliliter er lig med en kubikcentimeter.

Antag for eksempel, at du startede med 35 ml vand og sluttede med 65 ml vand; volumen af dit objekt er så 65 – 35 = 30 ml eller 30 cm

Del 3 af 3: Beregning af tæthed

Billede med titlen Calculate Volume and Density Step 9.jpg

1. Bestem massen af objektet. Mængden af stof i et objekt er massen af det objekt. Dette kan måles direkte ved at placere objektet på en skala med enheden i gram.

Hav en nøjagtig skala ved hånden, og placer genstanden på den. Notér dens masse i din notesbog.
Du kan også måle masse med en vægt. Med genstanden på den ene side placeres vægte med kendt masse på den anden side af vægten, indtil de er i ligevægt med genstanden. Massen af dit objekt er lig med vægtens samlede masse.
Det er vigtigt at sikre, at dit emne er tørt, før du vejer det. På den måde er du sikret, at måleresultatet ikke er mindre præcist på grund af det optagne vand.

Billede med titlen Calculate Volume and Density Step 10.jpg

2. Beregn volumen af dit objekt. Hvis dit objekt har en regulær form, skal du beregne volumen ved hjælp af en af de tidligere angivne metoder. Hvis formen er uregelmæssig, beregnes volumenet ved hjælp af forskydningsmetoden som forklaret ovenfor.

Billede med titlen Calculate Volume and Density Step 11.jpg

3. Beregn massefylden. Massefylde er defineret som massen divideret med volumen. Til sidst, for at bestemme massefylden, divideres den vægtede masse med det målte volumen. Resultatet er densiteten af metallet udtrykt i g/cm.

Beregn f.eks. tætheden

ρ

$rho$ af et stof med et volumen på 8 cm og en masse på 24 g.

\begin{matrix} ρ & = \end{matrix} \frac{m}{V} = 24 g 8 c m 3 = 3 g c m - 3

${begin{aligned}rho &={frac{M}{V}}\&={frac{24{{rm { g}}}}{8{{rm { cm^{{3}}}}}}}\&=3{{rm { g cm^{{-3}}}}}end{aligned}}$

Tips

Du kan teste dine volumenberegninger ved at sammenligne resultatet af forskydningsmetoden og beregningerne.
Objekter er ofte en samling af flere geometriske objekter, så du kan opdele dem i mindre grundlæggende grupper for at bestemme volumen af hver og derefter lægge dem alle sammen for at bestemme objektets volumen.