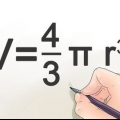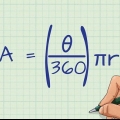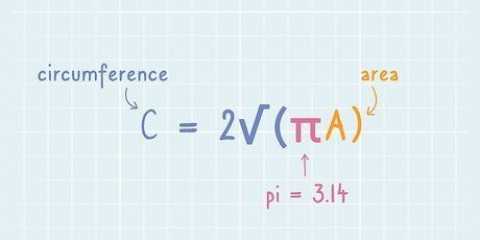Antag, at du får at vide, at der er en kugle med en radius på 10 cm. Find lydstyrken på følgende måde: 





Som et eksempel på denne beregning skal du bestemme volumenet af en kugle med en diameter på 10 cm. 















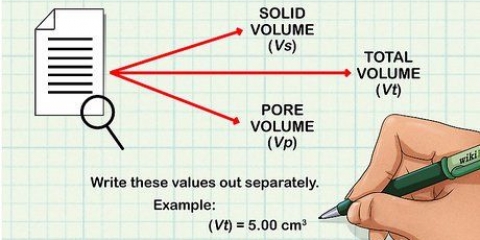
Hæld nok vand i koppen til at dække pæren. Bemærk lydstyrken. Hæld pæren i vandet. Bemærk at vandstanden stiger. Bemærk den nye lydstyrke. Træk det første bind fra det andet. Resultatet er kuglens rumfang. Antag, at din vandstand stiger fra 100 ml til 625 ml, når du sænker pæren. Så volumen er 525 ml. Bemærk at 1 ml=1 cm. 

Alle eksempler i det foregående afsnit resulterede i volumener målt i kubikcentimeter. Den angivne tæthedstabel giver dog tætheder baseret på kubikmeter. Fordi der er 100 centimeter i en meter, er der 10 kubikcentimeter i en kubikmeter. Divider de givne tætheder med 10 for at få densiteten i enheder af kg/cm (det gøres nemt ved at flytte decimaltegnet seks mellemrum til venstre). For de fire tidligere nævnte materialer er de konverterede tætheder som følger: Aluminium = 2700 kg/m = 0,0027 kg/cm Smør = 870 kg/m3 = 0,00087 kg/cm bly = 11.350 kg/m = 0,01135 kg/cm Presset træ = 190 kg/m = 0,00019 kg/cm 
Ved hjælp af de fire tidligere nævnte materialer, aluminium, smør, bly og presset træ, bestemmer man massen af en kugle med et rumfang på 500 cm. 






Du læser også, at kuglen er lavet af messing. Du skal slå tætheden af messing op i din Binas eller fra en anden kilde. På hjemmesiden EngineeringToolbox.com, kan du slå op, at massefylden af messing er 8480 kg/m. Da kuglens diameter er angivet i meter, er dens volumen beregnet i kubikmeter, så du ikke behøver at omregne tætheden. 









Beregn massen af en kugle
Indhold
Kort sagt er en kugle en solid rund bold. For at beregne massen af en kugle skal du kende kuglens størrelse (volumen) og dens tæthed. Du kan beregne volumenet ved at bruge kuglens radius, omkreds eller diameter. Du kan også nedsænke kuglen i vand for at finde volumen ved vandforskydning. Hvis du kender rumfanget, kan du gange det med massefylden for at finde massen.
Trin
Del 1 af 3: Bestemmelse af rumfanget af en kugle

1. Brug formlen for rumfanget af en kugle. En kugle er et cirkulært fast stof i tre dimensioner. Den primære formel for rumfanget af en kugle er:

2. Find rumfanget af en kugle, hvis du kender dens radius. Radius af en kugle er målet fra midten af kuglen til den ydre kant. Hvis du får et problem med at beregne volumen, så er radius sandsynligvis givet. Ellers kan radius være svær at måle, fordi man ikke præcist kan bestemme midten af en fast genstand.





3. Bestem volumen, hvis diameteren er angivet. En anden mulighed er, at for en bestemt situation er diameteren af en kugle givet. Diameteren er lig med to gange radius. Faktisk er diameteren afstanden fra den ene kant af kuglen gennem midten til den anden kant. For at beregne volumen ud fra diameter (d), revider formlen som følger:







4. Revider formlen, hvis du kender omkredsen. Omkredsen af en kugle er nok den nemmeste at måle direkte. Du kan bruge et målebånd, vikle det forsigtigt rundt om den bredeste del af pæren og tage målet. Måske er omkredsen angivet i en erklæring. For at finde volumen, der starter med omkredsen (C), skal du revidere formlen som følger:





5. Beregn volumen, hvis du kender omkredsen. Antag, at du får en kugle, og du måler omkredsen til 32 cm. Find lydstyrken på følgende måde:





6. Mål volumen ved vandfortrængning. En sidste praktisk metode til at måle volumen er at nedsænke pæren i vand. Du skal have et bæger, der er stort nok til at nedsænke pæren med nøjagtige volumenmarkeringer.
Del 2 af 3: Beregning af masse ud fra volumen

1. Bestem tætheden. For at beregne massen ud fra rumfanget skal du kende genstandens tæthed. Forskellige materialer har forskellige tætheder. Overvej for eksempel en kugle af styrofoam og sammenlign dens vægt med en kugle af samme størrelse jern. Jern har en meget større tæthed og vil derfor have en større masse.
- Du kan slå tætheder op af mange faste materialer online, i lærebøger eller i en Binas.
- For eksempel, her er de registrerede tætheder af nogle faste materialer:
- Aluminium = 2700 kg/m
- Smør = 870 kg/m
- bly = 11.350 kg/m
- Presset træ = 190 kg/m

2. Konverter enhederne efter behov. De enheder, du bruger ved beregning af volumen, skal svare til volumenhederne i den målte massefylde. Hvis ikke, så skal du konvertere dem.

3. Gang volumen med massefylden for at finde massen. Formlen for tætheden er  , som du måske husker. Hvis du omarrangerer dette for at finde massen, bliver ligningen
, som du måske husker. Hvis du omarrangerer dette for at finde massen, bliver ligningen  .
.
 , som du måske husker. Hvis du omarrangerer dette for at finde massen, bliver ligningen
, som du måske husker. Hvis du omarrangerer dette for at finde massen, bliver ligningen  .
.



Del 3 af 3: Løsning af et eksempelproblem

1. Læs opgaven grundigt. Når du besvarer problemer med masseberegninger, skal du læse hele udsagnet omhyggeligt. Mens du læser, kan det hjælpe at fremhæve indlægget. Læs hele problemet omhyggeligt for at se, hvad du bliver bedt om at løse. Overvej for eksempel følgende problem:
- En stor kugle af massiv messing har en diameter på 1,2 m. Bestem massen af kuglen.

2. Organiser de kendte og ukendte data. Hvis du læser udsagnet omhyggeligt, kan du bestemme, at diameteren er givet, så brug den modificerede formel:


3. Beregn volumen. For at beregne volumen skal du indtaste den relevante formel, udfylde de data, du kender, og udføre beregningerne som følger:






4. Brug massefylde til at beregne masse. Tænk det  . Indtast de værdier, du kender, i formlen for at finde massen:
. Indtast de værdier, du kender, i formlen for at finde massen:
 . Indtast de værdier, du kender, i formlen for at finde massen:
. Indtast de værdier, du kender, i formlen for at finde massen:


Tips
- Denne forklaring antager, at kuglens tæthed er den samme overalt. Dette antages i de fleste matematiske og fysikproblemer. Det er dog muligt, at kernen af en kugle er lavet af andet materiale end overfladen.
Artikler om emnet "Beregn massen af en kugle"
Оцените, пожалуйста статью
Populær