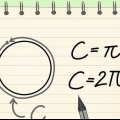Beregning af omkreds efter område: 10 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Brug af perimeterligningen
- Metode 2 af 2: Løs problemet omvendt

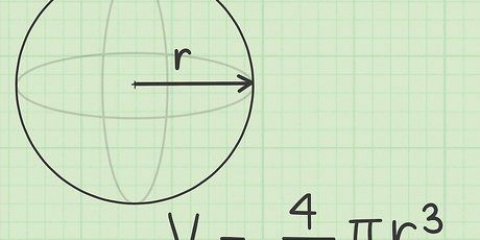
Formlen til at beregne omkredsen (C) af en cirkel, C = πD eller C = 2πR, er enkel, hvis du kender cirklens diameter (D) eller radius (R). Men hvad gør du, hvis du kun kender området af cirklen? Ligesom mange ting i matematik er der flere løsninger på dette problem. Formlen C = 2√πA er designet til at finde omkredsen af en cirkel ved hjælp af arealet (A). Du kan også vende ligningen A = πR for at finde R, og derefter indtaste R i perimeterligningen. Begge ligninger giver det samme resultat.

Trin

Metode 1 af 2: Brug af perimeterligningen

1. Brug formlen C=2√πA til at løse problemet. Denne formel beregner omkredsen af en cirkel, hvis du kun kender dens areal. C står for omkredsen og A for området. Skriv denne formel for at begynde at løse problemet.

π-symbolet, som står for pi, er en gentagende decimal med (nu) tusindvis af cifre efter decimalkommaet. For nemheds skyld skal du bruge 3.14 som værdien af pi.
Da du alligevel skal konvertere pi til dens numeriske form, skal du bruge 3.14 i ligningen fra starten. Skriv det som C = 2√3,14 x A.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens område Trin 2

2. Inkluder arealet som A i ligningen. Da du allerede kender arealet af cirklen, er det værdien af A. Fortsæt derefter med at løse problemet ved at bruge rækkefølgen af operationer.

Lad os sige, at området af cirklen er 500 cm. Derefter regner du ligningen ud som følger: 2√3,14 x 500.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens område Trin 3

3. Multiplicer pi med arealet af cirklen. I rækkefølgen af operationer kommer operationerne inden for kvadratrodssymbolet først. Multiplicer pi med arealet af den cirkel, du tilsluttede. Sæt derefter resultatet ind i ligningen.

Hvis udregningen er lig med 2√3,14 x 500, så beregner du først 3,14 x 500 = 1570. Beregn derefter 2√1.570.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens areal Trin 4

4. Særligkvadrat rod af summen. Der er flere måder at beregne kvadratroden på. Hvis du bruger en lommeregner, skal du trykke på funktionen √ og indtaste tallet. Du kan også løse problemet manuelt ved at bruge prime faktorer.

Kvadratroden af 1570 er 39,6.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens område Trin 5

5. Gang kvadratroden med 2 for at finde omkredsen. Til sidst afslutter du udregningen ved at gange resultatet med 2. Dette returnerer et endeligt tal, omkredsen.

Beregn 39,6 x 2 = 79,2. Det betyder, at omkredsen er 79,2 cm, hvilket løser formlen.

Metode 2 af 2: Løs problemet omvendt

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens område Trin 6

1. Brug formlen A = πR in. Dette er formlen for arealet af en cirkel. A står for arealet og R for radius. Normalt ville du bruge det, hvis du kendte radius, men du kan også udfylde området for at løse ligningen.

Brug igen 3,14 som den afrundede værdi for pi.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens område Trin 7

2. Indtast området som værdi for A. Brug arealet af cirklen i ligningen. Placer dette til venstre for ligningen som værdien for A.

Antag, at arealet af cirklen er 200 cm. Ligningen bliver så 200 = 3,14 x R.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens område Trin 8

3. Divider begge sider af ligningen med 3,14. For at løse denne form for ligning skal du gradvist eliminere trinene til højre ved at udføre de modsatte operationer. Da du kender værdien af pi, dividerer du hver side med denne værdi. Dette eliminerer pi til højre og giver dig en ny numerisk værdi til venstre.

Hvis du dividerer 200 med 3,14, er resultatet 63,7. Så den nye ligning er 63,7 = R.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens område Trin 9

4. Særligkvadrat rod af resultatet for at få radius af cirklen. Så er eksponenten på højre side af ligningen elimineret. Det modsatte af `eksponentiering` er at finde kvadratroden af tallet. Find kvadratroden af hver side af ligningen. Dette fjerner eksponenten til højre og sætter radius til venstre.

Kvadratroden af 63,7 er 7,9. Ligningen bliver så 7,9 = R, hvilket betyder at cirklens radius er 7,9. Dette vil give dig al den information, du behøver for at finde omkredsen.

Billede med titlen Find omkredsen af en cirkel ved hjælp af dens areal Trin 10

5.Bestem omkredsen af cirklen ved hjælp af radius. Der er to formler til at finde omkredsen (C). Den første er C = πD, hvor D er diameteren. Gang radius med 2 for at finde diameteren. Den anden er C = 2πR. Gang 3,14 med 2 og gange derefter resultatet med radius. Begge formler vil give dig det samme resultat.

Brug den første mulighed, 7,9 x 2 = 15,8, diameteren af cirklen. Denne diameter gange 3,14 er 49,6.

For den anden mulighed bliver beregningen 2 x 3,14 x 7,9. Først beregner du 2 x 3,14 = 6,28, og det ganget med 7,9 er 49,6. Læg mærke til, hvordan begge metoder giver dig det samme svar.