Optag denne måling som -en. Eksempel: a = 2 cm 
Bemærk, at dette trin beregner arealet af en flade af terningen. Eksempel: a = 2 cm a = 2 x 2 = 4 cm 
Dette trin afslutter beregningen af terningens areal. Eksempel: a = 4 cm Areal = 6 x a = 6 x 4 = 24 cm 

Mål længden af basen for at bestemme længden af prismet, og tildel det til c. Eksempel: c = 5 cm Mål bredden af basen for at bestemme bredden af prismet, og kald det -en. Eksempel: a = 2 cm Mål højden på siden for at bestemme prismets højde, og kald det b. Eksempel: b = 3 cm 
Eksempel: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm 
Eksempel: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm 
Eksempel: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm 
Eksempel: Areal = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm. 

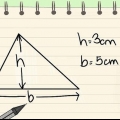
Basen b, er lig med længden af trekantens bund. Eksempel: b = 4 cm Højden h af den trekantede base er lig med afstanden mellem den nederste kant og spidsen. Eksempel: h = 3 cm Arealet af en trekant ganget med 2 = 2(1/2)b*h = b*h = 4*3 =12 cm 
Eksempel: H = 5 cm De tre sider refererer til de tre sider af den trekantede base. Eksempel: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm 
Eksempel: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm 
Eksempel: P x H = 12 x 5 = 60 cm 
Eksempel: 2A + PH = 12 + 60 = 72 cm. 

Eksempel: r = 3 cm 
Eksempel: r = r x r = 3 x 3 = 9 cm 
Eksempel: π*r = 3,14 x 9 = 28,26 cm 
Eksempel: 4π*r = 4 x 28,26 = 113,04 cm 

Eksempel: r = 3 cm Eksempel: h = 5 cm 
Eksempel: Areal af basen = π*r = 3,14 x 3 x 3 = 28,26 cm Eksempel: 2π*r = 2 x 28,26 = 56,52 cm 
Eksempel: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 cm 
Eksempel: 2π*r + 2π*rh = 56,52 + 94,2 = 150,72 cm 

Eksempel: l = 3 cm Eksempel: s = 1 cm 
Eksempel: s = s x s = 1 x 1 = 1 cm 
Eksempel: 2 x s x l = 2 x 1 x 3 = 6 cm 
Eksempel: s + 2 lm = 1 + 6 = 7 cm 

Eksempel: r = 2 cm Eksempel: h = 4 cm 
Eksempel: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm 
Eksempel: π*r = 3,14 x 2 x 2 = 12,56 cm 
Eksempel: π*rl = 3,14 x 2 x 4,47 = 28,07 cm 
Eksempel: π*r + π*rl = 12,56 + 28,07 = 40,63 cm
Beregn areal
Indhold
Arealet er det samlede rum, der optages af alle områder af et objekt. Det er summen af alle områder af det pågældende objekt. At bestemme arealet af en tredimensionel form er ret let, så længe du bruger den rigtige formel. Hver form har sin egen separate formel, så du skal først tjekke, hvilken form det er. Beregning af arealformlen for forskellige objekter kan gøre beregninger lettere i fremtiden. Her diskuterer vi nogle af de mest almindelige former, du kan støde på.
Trin
Metode 1 af 7: Terning

1. Definer formlen for arealet af en terning. En terning har seks identiske flader. Da både længden og bredden af en firkant er ens, er arealet af en firkant -en, hvorved -en længden er den ene side. Da en terning har seks lige store flader, kan du beregne dens areal ved at gange arealet af en af dens flader med seks. Formlen for arealet af en terning O er O = 6a, hvorved -en længden er den ene side.
- Arealenhederne er en vis længde i anden kvadrat: cm, dm, m osv.

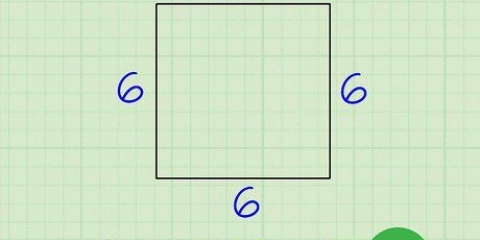
2. Mål længden af den ene side. Per definition skal hver side eller kant (kant) af en terning være lig med den anden, så du behøver kun at måle den ene side. Mål længden af siden med en lineal. Vær opmærksom på de enheder, du bruger.

3. Kvadret din måling til -en. Kvadret målingen for at beregne længden af ribben. At kvadrere en værdi betyder at gange den med sig selv. Hvis du lærer dette for første gang, kan det være nyttigt at huske dette som NT= 6*a*a.

4. Gang dette produkt med seks. Husk, at en terning har seks identiske flader. Nu hvor du kender arealet af en af ansigterne, skal du gange det med seks (på grund af alle seks ansigter).
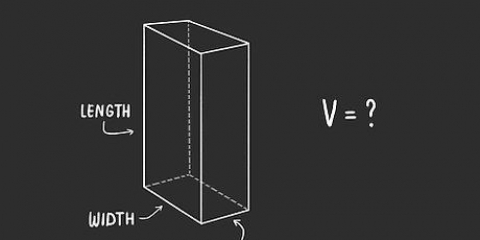
Metode 2 af 7: Rektangulært prisme

1. Definer formlen for arealet af et rektangulært prisme. Ligesom en terning har et rektangulært prisme seks flader, men i modsætning til en terning er disse flader ikke ens. I et rektangulært prisme er kun de modsatte flader lig med hinanden. Derfor, når man beregner arealet af et rektangulært prisme, skal de forskellige længder af ribberne tages i betragtning, som i formlen SA = 2ab + 2bc + 2ac.
- For denne formel, -en lig med prismets bredde, b lig med højden og c lig med længden.
- Hvis vi ser nærmere på formlen, vil du se, at vi ganske enkelt lægger alle områderne sammen på hver flade af objektet.
- Arealenheden vil være en vis længde i kvadrat: cm, dm, m osv.

2. Mål længden, højden og bredden af hver side. Alle tre aflæsninger kan være forskellige, så hver skal måles separat. Mål hver side med en lineal og noter værdien. Brug de samme enheder til hver måling.

3. Beregn arealet af en af prismets flader, og gang det med to. Husk, at der er seks flader i et rektangulært prisme, og de modsatte flader er lig med hinanden. Gang længden og højden, eller c og -en, at finde arealet af et fly. Tag denne måling og gang den med to for at tage højde for det modsatte identiske plan.

4. Find arealet af den anden side af prismet og gang det med to. Som med det første sæt ansigter skal du gange bredden og højden, eller -en og b til bestemmelse af arealet af en anden flade af prismet. Multiplicer denne måling med to for at tage højde for de modsatte identiske sider.

5. Beregn arealet af prismets ender og gang det med to. Prismets to andre flader er enderne. Gang længden og bredden (c og b) for at finde deres overflade. Multiplicer dette område med to for at tage højde for begge sider.

6. Tilføj de tre separate områder sammen. Da arealet af prismet er det samlede areal af alle flader af et objekt, er det sidste trin at lægge alle individuelt beregnede arealer sammen. Læg arealerne på alle sider sammen for at få det samlede areal.
Metode 3 af 7: Trekantet prisme

1. Definer arealformlen for et trekantet prisme. Et trekantet prisme har to identiske trekantede flader og tre rektangulære flader. For at finde området skal du beregne arealet af alle ansigterne og lægge dem sammen. Arealet af et trekantet prisme er SA = 2A + PH, hvor A er arealet af den trekantede base, P er omkredsen af den trekantede base, og h er højden af prismet.
- For det holder denne formel -en det areal af en trekant og dermed A = 1/2 bh, hvorved b er bunden af trekanten og h højden.
- s er trekantens omkreds beregnet ved at addere alle tre kanter af trekanten.
- Arealenhederne er en længdeenhed i kvadrat: cm, dm, m osv.

2. Beregn arealet af det trekantede plan og gang det med to. Arealet af en trekant er /2b*h hvor b er trekantens basis og h er højden. Så da der er to identiske trekanter som flader, multiplicerer vi formlen med to. Dette gør beregningen for begge fly let (b*h).

3. Mål hver side af trekanten og højden af prismet. For at fuldføre arealberegningen skal du kende længden af hver side af trekanten og højden af prismet. Højden er afstanden mellem de to trekantede flader.

4. Find omkredsen af trekanten. Omkredsen af trekanten kan beregnes ved at lægge alle de målte sider sammen: S1 + S2 + S3.

5. Multiplicer omkredsen af basen med prismets højde. Husk, at prismets højde er afstanden mellem de to trekantede flader. Med andre ord multiplicer s af huh.

6. Tilføj de to separate aflæsninger sammen. Du skal tilføje de to målinger fra de to foregående trin sammen for at få arealet af det trekantede prisme.
Metode 4 af 7: Bol

1. Definer arealformlen for en kugle. En kugle har en buet overflade, så overfladearealet er en værdi ganget med konstanten pi. Arealet af en kugle beregnes ved hjælp af ligningen NT = 4π*r.
- For denne formel, r lig med kuglens radius. Pi (eller π) kan afrundes til 3,14.
- Arealets enheder vil være en længdeenhed i kvadrat: cm, dm, m osv.

2.Mål radius af pæren. Kuglens radius er halvdelen af diameteren eller afstanden fra kuglens centrum til kanten.

3. Firkant radius. For at kvadrere et tal skal du gange det med sig selv. Multiplicer målingen for r med sig selv. Husk at denne formel kan omskrives som SA = 4π*r*r.

4. Gang den kvadrerede radius med en afrunding af pi. Pi er en konstant, der repræsenterer forholdet mellem en cirkels omkreds og dens diameter. Det er et irrationelt tal med mange cifre efter decimalkommaet. Det er ofte afrundet til 3,14. Multiplicer den kvadratiske radius med π eller 3,14 for arealet af et cirkulært tværsnit af kuglen.

5. Gang dette produkt med fire. For at fuldføre beregningen skal du gange den med fire. Find arealet af kuglen ved at gange det flade cirkulære område med fire.
Metode 5 af 7: Cylinder

1. Definer arealformlen for en cylinder. En cylinder har to cirkulære ender, der lukker en rørformet overflade. Formlen for arealet af en cylinder er NT = 2π*r + 2π*rh, hvorved r er lig med radius af den cirkulære base og h er lig med cylinderens højde. rund pi (eller π) falder til 3,14.
- Formlen 2π*r beregner arealet af de to cirkulære ender, mens 2πrh er arealet af kolonnen mellem de to ender.
- Arealenhederne er en længdeenhed i kvadrat: cm, dm, m osv.

2. Mål cylinderens radius og højde. Radius af en cirkel er halvdelen af dens diameter eller afstanden fra cirklens centrum til kanten. Højden er cylinderens samlede afstand fra den ene ende til den anden. Tegn disse mål med en lineal og skriv dem ned.

3. Find arealet af grundfladen og gang det med to. For at finde arealet af basen skal du bruge arealformlen eller en cirkel (π*r). For at fuldføre beregningen skal du kvadrere radius og gange den med pi. Derefter ganges med to på grund af den anden identiske cirkel i den anden ende af cylinderen.

4. Beregn selve cylinderens overflade med 2π*rh. Dette er formlen til at beregne arealet af et rør. Røret er mellemrummet mellem cylinderens to cirkulære ender. Gang radius med to, pi og højden.

5. Tilføj de to separate aflæsninger sammen. Tilføj arealet af de to cirkler til arealet af rummet mellem de to cirkler for at beregne cylinderens samlede areal. Bemærk: Når du tilføjer disse to stykker, genkender du den originale formel: NT =2π*r + 2π*rh.
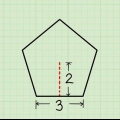
Metode 6 af 7: Firkantet pyramide

1. Definer arealformlen for en kvadratisk pyramide. En firkantet pyramide har en firkantet base og fire trekantede sider. Som nævnt er arealet af en firkant længden af den ene side i kvadrat. Arealet af en trekant er 1/2sl (siden af trekanten gange længden eller højden af trekanten). Da der er fire trekanter, beregner du det samlede areal ved at gange det med fire. Tilføjelse af alle disse flader sammen giver ligningen for arealet for en firkantet pyramide: NT = s + 2 kanal.
- I denne ligning, s længden af hver side af den firkantede base og l skråhøjden af hver trekantede side.
- Arealenheden er en bestemt længdeenhed i kvadrat: cm, dm, m osv.

2. Mål den skrå højde og bundside. Den skrå højde l, er højden af en af de trekantede sider. Det er afstanden fra bunden til spidsen af pyramiden, målt langs en flad side. Den grundlæggende side s, er længden af den ene side af kvadratbunden. Da basen er kvadratisk, er denne måling den samme for alle sider. Brug en lineal til hver måling.

3. Find arealet af den kvadratiske base. Arealet af en kvadratisk base kan beregnes ved at kvadrere længden af en side (s gange med sig selv).

4. Beregn det samlede areal af de fire trekantede flader. Den anden del af ligningen er arealet af de resterende fire trekantede flader. Ved hjælp af formlen 2ls multiplicerer vi s af l og to. Find området af hvert ansigt.

5. Tilføj de to separate områder sammen. Tilføj det samlede areal af ansigterne til arealet af basen for at beregne det samlede areal.
Metode 7 af 7: Kegle

1. Definer arealformlen for en kegle. En kegle har en cirkulær base og en rund overflade, der tilspidser i et punkt. For at finde området skal du tage arealet af den cirkulære base og arealet af keglen og lægge de to sammen. Formlen for arealet af en kegle er: SA = π*r + π*rl, hvorved r radius er fra den cirkulære base, l keglens skrå højde, og π er konstanten pi (3.14).
- Arealenheden er en bestemt længdeenhed i kvadrat: cm, dm, m osv.

2. Mål radius og højde af keglen. Radius er afstanden fra midten af den cirkulære base til kanten af basen. Højde er afstanden fra midten af basen til spidsen af keglen, målt gennem midten af keglen.

3. Beregn hældningshøjden (l) af keglen. Da den skrå højde er den faktiske hypotenus i en trekant, skal du finde ved hjælp af Pythagoras` sætning for at beregne det. Brug den omarrangerede form, l = √ (r + h), hvorved r radius er og h højden af keglen.

4. Find arealet af den cirkulære base. Arealet af basen beregnes med formlen π*r. Efter at have målt radius, kvadrerer du den (så du multiplicerer den med sig selv) og derefter gange du produktet med pi.

5. Beregn arealet af toppen af keglen. Brug formlen π*rl, hvor r radius er af cirklen og l hældningen som beregnet ovenfor for at bestemme arealet af toppen af keglen.

6. Tilføj de to områder sammen for at få det samlede areal af keglen. Beregn det endelige areal af keglen ved at tilføje arealet af den cirkulære base, når du beregner det forrige trin.
Fornødenheder
- Lineal
- Pen eller blyant
- Papir
Artikler om emnet "Beregn areal"
Оцените, пожалуйста статью
Populær