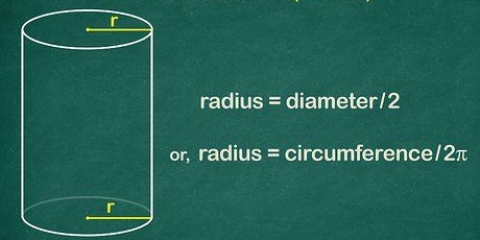
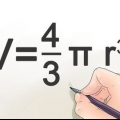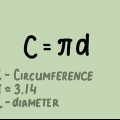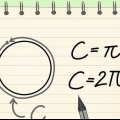Har du en kugle med en omkreds på 20 m, finder du radius med 20/2π = 3,183 m. Du kan bruge den samme formel til at konvertere mellem radius og omkreds af en cirkel. 
Hvis du har en kugle med et volumen på 100 cm, får du radius som følger: ((V/π)(3/4)) = r ((100/π)(3/4)) = r ((31.83)(3/4)) = r (23.87) = r 2,88 = r 
Hvis du har en kugle med et areal på 1200 cm, beregner du radius som følger: √(A/(4π)) = r √(1200/(4π)) = r √(300/(π)) = r √(95,49) = r 9,77 cm = r 

D = 2r. Ligesom cirkler er diameteren af en kugle to gange dens radius. C = πD eller 2πr. Ligesom cirkler er omkredsen af en kugle lig med π gange diameteren. Da diameteren er to gange radius, kan vi også sige, at omkredsen er lig med to gange radius gange π. V = (4/3)πr. Rumfanget af en kugle er dens radius til terningen (r x r x r), gange π, gange 4/3. A = 4πr. Arealet af en kugle er dens radius til anden potens (r x r), gange π, gange 4. Da omkredsen af en cirkel er lig med πr, kan det også siges, at arealet af en kugle er lig med fire gange arealet af en cirkel, som dannet af dens omkreds. 

I forbindelse med vores eksempelopgave slår vi fast, at pointen (3, 3, 0) på kuglens overflade, er givet. Ved at beregne afstanden mellem dette punkt og centrum kan vi finde radius. 
I vores eksempel erstatter vi (4, -1, 12) med (x1,y1,z1) og (3, 3, 0) for (x2,y2,z2), hvor vi løser dette på følgende måde: d = √((x2 - x1) + (y2 - y1) + (z2 - z1)) d = √((3 - 4) + (3 - -1) + (0 - 12)) d = √((-1) + (4) + (-12)) d = √(1 + 16 + 144) d = √(161) d = 12,69. Dette er radius af vores sfære. 
Ved at kvadrere begge sider af denne ligning får vi: r = (x2 - x1) + (y2 - y1) + (z2 - z1). Bemærk: Dette svarer i det væsentlige til standardligningen for en kugle (r = x + y + z), forudsat at dens centrum er lig med (0,0,0).
Beregning af radius af en kugle
Indhold
Radius af en kugle (forkortet som variablen r eller R) er afstanden fra kuglens nøjagtige centrum til et punkt på overfladen af kuglen. Ligesom cirkler, radius af en kugle er ofte et væsentligt første data for beregningen af en kugles diameter, omkreds, areal og volumen. Du kan dog også arbejde baglæns fra diameter, omkreds mv. for at finde kuglens radius. Brug den formel, der passer til de data, du har.
Trin
Metode 1 af 3: Brug af radiusformler

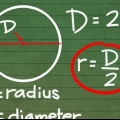
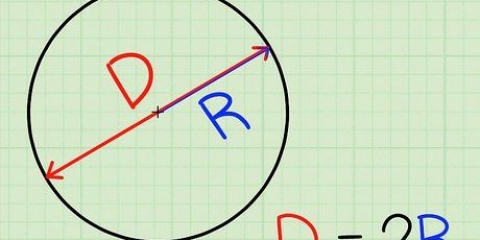
1. Bestem radius, hvis du kender diameteren. Radius er en halv diameter, så du bruger formlen r = D/2. Dette er identisk med metoden til at beregne radius af en cirkel givet diameteren.
- Hvis du har en kugle med en diameter på 16 cm, beregner du radius med 16/2 = 8 cm. Hvis diameteren er 42, så radius 21.

2. Bestem radius, hvis du kender omkredsen. Brug formlen C/2π. Da omkredsen er lig πD, som igen er lig med 2πr, beregner man radius ved at dividere omkredsen med 2π.

3. Beregn radius, hvis du kender kuglens rumfang. Brug formlen ((V/π)(3/4)). Rumfanget af en kugle er afledt af ligningen V = (4/3)πr.Ved at løse ligningen for r får man ((V/π)(3/4)) = r, så det bliver tydeligt, at en kugles radius er lig med rumfanget divideret med π, gange 3/4 , til 1/3 magt (eller terningerod).

4. Bestem overfladens radius. Brug formlen r = √(A/(4π)). Arealet af en kugle beregnes ved hjælp af ligningen A = 4πr. Løsning af ligningen for r giver √(A/(4π)) = r, hvilket betyder, at radius af en kugle er lig med kvadratroden af dens areal divideret med 4π. Du kan også tænde (A/(4π)) til 1/2 for det samme resultat.
Metode 2 af 3: Definition af nøgletermer

1. Kend de grundlæggende dimensioner af en kugle. Radius (r) er afstanden fra kuglens nøjagtige centrum til ethvert punkt på kuglens overflade. Generelt kan du finde radius af en kugle, hvis du kender dens diameter, omkreds, volumen eller areal.
- Diameter (D): længden af linjen gennem midten af en kugle & ndash; dobbelt radius. Diameteren er længden af en linje gennem midten af kuglen: fra et punkt på ydersiden af kuglen til et tilsvarende punkt lige overfor den. Med andre ord den størst mulige afstand mellem to punkter på kuglen.
- Omkreds (C): den endimensionelle afstand omkring kuglen på det bredeste sted. Med andre ord, omkredsen af det cirkulære tværsnit af en kugle, hvis plan passerer gennem midten af kuglen.
- Volumen (V): det tredimensionelle rum i kuglen. Det er "plads optaget af kuglen".
- Område (A): det todimensionelle rum på den ydre overflade af kuglen. Mængden af fladt rum, der dækker ydersiden af kuglen.
- pi (π): en konstant, der udtrykker forholdet mellem cirklens omkreds og cirklens diameter. De første 10 cifre i Pi er altid 3.141592653, selvom dette normalt afrundes til 3.14.

2. Brug forskellige aflæsninger til at bestemme radius. Du kan bruge diameter, omkreds, volumen og areal til at beregne radius af en kugle. Hvis du kender længden af radius, kan du beregne et hvilket som helst af disse tal. Så for at finde radius kan du vende formlerne til beregning af disse dele. Lær formlerne, der involverer radius til at beregne diameter, omkreds, areal og volumen.
Metode 3 af 3: Find radius som afstanden mellem to punkter

1. Bestem koordinaterne (x, y, z) for kuglens centrum. En måde at tænke på en kugles radius er som afstanden mellem kuglens centrum og ethvert punkt på dens overflade. Da dette er sandt, kan du bestemme kuglens radius ved hjælp af koordinaterne for midten og et punkt på kuglens overflade ved at beregne afstanden mellem de to punkter ved hjælp af en variant af standardafstandsformlen. For at starte skal du finde koordinaterne for kuglens centrum. Bemærk, at en kugle er tredimensionel, dette vil være et (x, y, z) punkt i stedet for et (x, y) punkt.
- Dette er lettere at forstå med et eksempel. Antag, at en kugle er givet med som centrum(-1, 4, 12). I de næste par trin skal vi bruge dette punkt til at bestemme radius.

2. Bestem koordinaterne for et punkt på kuglens overflade. Så skal du bestemme (x, y, z) koordinaterne for et punkt på overfladen af kuglen. Dette er muligt hver punkt på overfladen af kuglen. Fordi per definition alle punkter på overfladen af en kugle er lige langt fra midten, kan du bruge et hvilket som helst punkt til at bestemme radius.

3. Bestem radius med formlen d = √((x2 - x1) + (y2 - y1) + (z2 - z1)). Nu hvor du kender kuglens centrum og et punkt på kuglens overflade, kan du finde ud af radius ved at beregne afstanden mellem dem. Brug den tredimensionelle afstandsformel d = √((x2 - x1) + (y2 - y1) + (z2 - z1)), hvor d er afstanden, (x1,y1,z1) repræsenterer koordinaterne for midtpunktet, og (x2,y2,z2) står for koordinaterne for punktet på overfladen, for at bestemme afstanden mellem begge punkter.

4. Ved, at generelt er r = √((x2 - x1) + (y2 - y1) + (z2 - z1)). I en kugle er hvert punkt på overfladen den samme afstand fra kuglens centrum. Lad os tage ovenstående tredimensionelle afstandsformel og erstatte variablen "d" ved variablen "r" af radius, så får vi en ligning, der giver os mulighed for at finde radius ved ethvert givet centrum (x1,y1,z1) og ethvert tilsvarende punkt på overfladen (x2,y2,z2).
Tips
- Rækkefølgen af operationer har betydning. Hvis du ikke er sikker på, hvordan matematikreglerne fungerer, og din lommeregner understøtter parenteser, så sørg for at bruge disse.
- Denne artikel blev oprettet, fordi dette emne var i høj efterspørgsel. Men hvis du prøver at forstå rumlig geometri for første gang, er det nok bedre at starte med den anden side: at beregne egenskaberne for en kugle, når dens radius er givet.
- Pi eller π er et græsk bogstav, der angiver forholdet mellem en cirkels diameter og dens omkreds. Det er et irrationelt tal og kan ikke skrives som et forhold mellem reelle tal. Der er mange tilnærmelser, og 333/106 giver pi til fire decimaler. I dag husker de fleste mennesker tilnærmelsen 3.14, som normalt er nøjagtig nok til daglige formål.
Artikler om emnet "Beregning af radius af en kugle"
Оцените, пожалуйста статью
Lignende
Populær