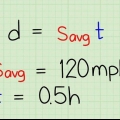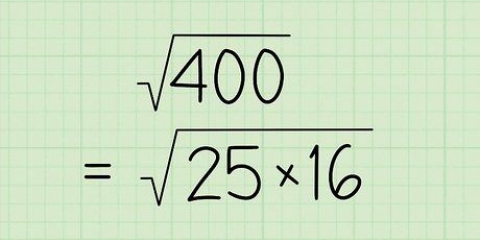I vores eksempel, lad os sige, at det er præcis klokken to koster at lave denne tur. 
I vores eksempel er denne ligning 100 miles/2 timer = 50 miles/timen(ca. 80 km/t). 
Enhederne for hastighed er afstandsenhederne over tidsenhederne. I vores eksempel er vores enheder miles/time (eller miles i timen), da vi målte afstand i miles og tid i timer. 

Lad os f.eks. sige, at i eksemplet ovenfor skal vi have vores svar ind miles i stedet for kilometer. Der er omkring 1,6 kilometer i en mile, så vi kan konvertere det sådan her: Bemærk, at fordi kilometer er nederst i brøken, kan den overstreges med kilometerne i det oprindelige svar, så svaret efterlades i miles. Denne webstedet indeholder konverteringer for de mest almindelige enheder. 
Lad os for eksempel sige, at et fly flyver fem gange i en cirkel, der er 20 miles bred. Flyet gennemfører denne rejse på en halv time. I dette eksempel skal vi stadig bestemme præcis, hvor langt flyet har rejst, før vi kan finde hastigheden. Vi kan bruge ligningen for afstanden omkring en cirkel (dens omkreds) i stedet for "-en" i vores sammenligning. Denne ligning er omkreds = 2πr hvor r = radius af cirklen. Vi kan løse dette på følgende måde: 
For at illustrere denne forskel, forestil dig den sidste rejse, du tog i en bil. Det er højst usandsynligt, at du har kørt den samme hastighed hele rejsen. I stedet startede du langsomt og nåede gradvist din tophastighed og satte farten ned ved lyskryds, trafikpropper og så videre. Hvis du bruger standardhastighedsligningen til at beregne din hastighed for turen, afspejles disse hastighedsændringer ikke. I stedet får du svar et sted mellem de forskellige hastigheder, du har kørt med. 

Af denne grund har begge biler i eksemplet ovenfor en hastighed (hastighed) ved 50 km/t. 
Antag, at et objekts position i meter er givet ved ligningen 3t + t - 4 hvor t = tid i sekunder. Vi vil gerne vide, hvad objektets hastighed er ved t = 4 sekunder. I dette tilfælde kan vi løse dette på følgende måde: Nu udfylder vi t = 4: 
Antag, at et objekt har en konstant acceleration (i m/s givet ved a (t) = -30. Lad os også sige, at objektet har en begyndelseshastighed på 10 m/s. Vi skal finde hastigheden ved t = 12s. I dette tilfælde kan vi løse dette på følgende måde: For at finde C løser vi for v(t) for t = 0. Husk, at objektets begyndelseshastighed er 10 m/s. Nu kan vi indtaste t = 12 sekunder.
Beregn hastighed
Indhold
Hastighed er et mål for `hvor hurtigt` noget går på et givet tidspunkt. Hvis du nogensinde har set på en bils speedometer, mens du kører, har du set, hvordan hastigheden måles - jo længere nålen går, jo hurtigere er bilens hastighed. Der er et par forskellige måder at beregne hastighed på, alt efter hvilke oplysninger du har. Til generelle formål er ligningen hastighed = distance/tid (eller s = a/t) normalt den nemmeste måde at beregne hastighed på.
Trin
Metode 1 af 3: Brug af standardhastighedsligningen

1. Find afstanden et objekt har tilbagelagt. Den grundlæggende ligning, som de fleste mennesker bruger til at finde ud af, hvor hurtigt noget går, er meget let at bruge. Det første du skal vide er hvor lang afstand objektet har tilbagelagt. Med andre ord, hvor langt er startpunktet fra slutpunktet?
- Denne ligning vil være lettere at forstå med et eksempel. Lad os sige, at vi tager en biltur til en forlystelsespark 100 miles (ca. 161 kilometer). I de næste par trin vil vi bruge denne information til at løse denne ligning.

2. Find den tid, det tog objektet at rejse denne afstand. Den næste information, du har brug for, er hvor lang tid det tog objektet at rejse. Med andre ord, hvor lang tid tog det at komme fra startpunktet til slutpunktet?

3. Divider afstanden med tiden for at finde hastigheden. Alt du behøver er disse to oplysninger for at bestemme din hastighed på rejsen. Afstanden om tiden giver dig objektets hastighed.

4. Glem ikke enhederne. Mærk dit svar med de relevante enheder (såsom miles i timen osv.) er kritisk. Uden enheder kan det være svært for andre mennesker at forstå, hvad dit svar betyder. Du kan også miste point, hvis du glemmer at skrive enheden ned på en skoleopgave.
Metode 2 af 3: Løsning af andre problemer

1. Isoler de forskellige variable for at beregne afstand og tid. Når du kender det grundlæggende i hastighedsligningen, kan du bruge den til at finde mere end blot hastighed. For eksempel, hvis du kender hastigheden og en af de andre variabler, kan du omarrangere ligningen for at finde den manglende information.
- Antag, at vi ved, at et tog har kørt med en hastighed på 20 kilometer i timen i fire timer, men vi skal vide, hvor langt det har kørt. I dette tilfælde kan vi omarrangere ligningen og løse den på denne måde:
- hastighed = distance/tid
- hastighed × tid = (afstand/tid) × tid
- hastighed × tid = afstand
- 20 km/t × 4 t = afstand = 80 kilometer

2. Konverter dine enheder om nødvendigt. Nogle gange kan du beregne hastigheden i en anden enhed, end du har brug for. I dette tilfælde bør du konverteringsfaktorer bruge til at sætte dit svar i den rigtige enhed. For at gøre dette skal du skrive relationerne mellem dine enheder som en brøk og gange. Når du multiplicerer, roterer du din brøk efter behov for at slippe af med de enheder, du ikke ønsker. Dette er meget nemmere end det lyder!
- 80 kilometer × 1 mile/1.6 kilometer = 50 miles

3. Erstat om nødvendigt variablen `afstand` med afstandsformler. Objekter rejser ikke altid i pæne, bekvemme lige linjer. Hvis ikke, er du muligvis ikke i stand til blot at indsætte en numerisk værdi for afstand i standardhastighedsligningen. I stedet skal du muligvis erstatte a`et i s = a/t med en formel, der modellerer den afstand, objektet har tilbagelagt.
- s = (2 × π × r)/t
- s = (2 × π × 10)/0.5
- s = 62.83/0.5 = 125.66 miles/timen

4. Se at s = a/t a gennemsnit hastighed giver. Den enkle, praktiske ligning, vi brugte til at finde hastigheden, har en stor fejl. Værdien den giver er teknisk set en gennemsnitshastighed. Det betyder, at det antager, at det objekt, du måler har samme hastighed under hele rejsen. Som vi vil se nedenfor, kan det være sværere at finde et objekts hastighed på et givet tidspunkt.
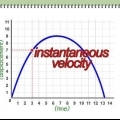
Metode 3 af 3: Beregning af øjeblikkelig hastighed
Bemærkning: Dette afsnit bruger teknikker ukendt for dem, der ikke har studeret calculus. Se vores kalkulusartikler for at få hjælp.

1. Bemærk, at hastighed er defineret som størrelsen af hastigheden. Højere niveau hastighedsberegninger kan være forvirrende, fordi matematikere og videnskabsmænd bruger forskellige definitioner for "hastighed". En hastighed (hastighed) har to komponenter: a størrelse og en retning. Størrelsen er lig med objektets hastighed. En retningsændring vil forårsage en ændring i hastighed (hastighed), men ikke i hastighed.
- Lad os f.eks. sige, at to biler kører i hver sin retning. Hastighedsmålerne på begge biler viser 50 km/t, så de har begge samme hastighed. Men da de flytter fra hinanden, kan vi sige, at en bil er en hastighed (hastighed) på -50 km/t og man har en hastighed (hastighed) fra 50 km/t.
- Ligesom du kan beregne den øjeblikkelige hastighed (hastighed), kan du også beregne beregne øjeblikkelig hastighed (hastighed).

2. Brug absolutte værdier for negative hastigheder. Objekter kan have hastigheder af negativ størrelse (hvis de bevæger sig i en negativ retning i forhold til noget andet). Men der er ikke sådan noget som en negativ hastighed (hastighed), så i disse tilfælde absolut værdi af størrelse ændrer objektets hastighed.

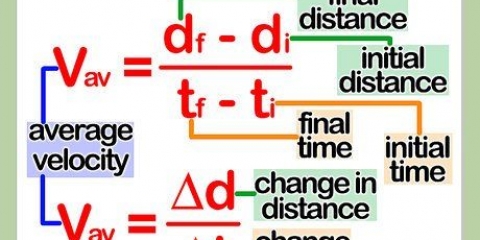
3. Tag den afledede af en positionsfunktion. Hvis du har en funktion s(t), der giver dig positionen af et objekt i forhold til tiden, så vil den afledede af s(t) give dig hastighed (hastighed) giver med hensyn til tid. Sæt bare en tidsværdi ind i denne ligning for variablen t (eller hvad tidsværdien nu er) for at få hastigheden på dette tidspunkt. Herfra er det nemt at finde hastigheden.
- 3t + t - 4
- s`(t) = 2 × 3t + 1
- s`(t) = 6t + 1
- s`(t) = 6(4) + 1 = 24 + 1 = 25 meter/sekund. Dette er teknisk set en hastighedsmåling (hastighed), men da den er positiv og retning ikke er nævnt i opgaven, kan vi i det væsentlige bruge den til hastighed.

4. Tag integralet af en accelerationsfunktion. Acceleration er en måde at ændring i et objekts hastighed over tid at måle. Dette emne er lidt for komplekst til fuldt ud at forklare i denne artikel. Det er dog nyttigt at bemærke, at når du har en funktion a(t), der giver acceleration i forhold til tid, giver integralet af a(t) dig hastighed (hastighed) i forhold til tid. Bemærk, at det er nyttigt at kende objektets begyndelseshastighed, så du kan definere konstanten, der er resultatet af et ubestemt integral.
- a(t) = -30
- v(t)= ∫ a(t)dt =∫ -30dt = -30t + C
- v(0) = 10 = -30(0) + C
- 10 = C, så v(t) = -30t + 10
- v(12) = -30(12) + 10 = -360 + 10 = -350. Da hastighed er den absolutte værdi af hastighed, er objektets hastighed 350 meter/sekund.
Tips
- Øvelse gør mester! Prøv at lave dine egne summer ved at erstatte forskellige tal i eksemplerne ovenfor.
- Hvis du leder efter en hurtig måde at beregne for avancerede hastighedsberegninger, så brug her end den online afledte lommeregner og den online integralberegner her.
Artikler om emnet "Beregn hastighed"
Оцените, пожалуйста статью
Populær