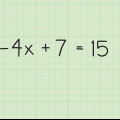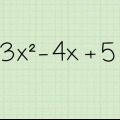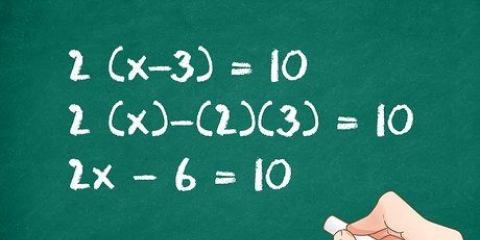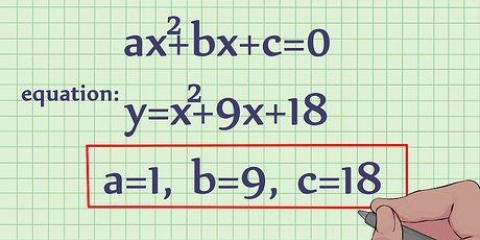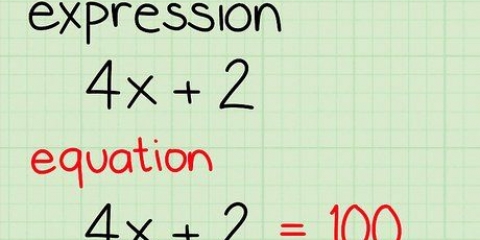Det er tydeligt her hvorfor  , fordi
, fordi  er i nævneren, og du kan ikke dividere med nul.
er i nævneren, og du kan ikke dividere med nul. Hvis du har brug for det, kan du forlænge venstre side for at sikre, at firkantningen fungerer. 

Nu kan vi slippe for de absolutte værditegn, ved  at placere til højre. Vi kan gøre dette, fordi den absolutte værdi ikke skelner mellem positive og negative tal, så de er begge gyldige. Denne detalje er grunden til, at andengradsligningen gør det muligt at få to rødder som et resultat.
at placere til højre. Vi kan gøre dette, fordi den absolutte værdi ikke skelner mellem positive og negative tal, så de er begge gyldige. Denne detalje er grunden til, at andengradsligningen gør det muligt at få to rødder som et resultat. 
Lad os forenkle dette udtryk lidt mere. Da kvadratroden af en kvotient er kvotienten af kvadratrødderne, kan vi skrive højre side som  Så kan vi tage kvadratroden af nævneren.
Så kan vi tage kvadratroden af nævneren. 


Lær kvadratinddeling
En af de vigtigste færdigheder for matematikstuderende er abc-formlen, eller 


Trin
1. Start med standardformen af en generel andengradsligning. Selvom enhver sammenligning med et udtryk som  i, er kvadratisk, sætter standardformen alt til nul. Huske på, at
i, er kvadratisk, sætter standardformen alt til nul. Huske på, at  er koefficienter, der kan være et hvilket som helst heltal, så nu kan du ikke udfylde tal for variablerne - vi vil arbejde med den generelle form.
er koefficienter, der kan være et hvilket som helst heltal, så nu kan du ikke udfylde tal for variablerne - vi vil arbejde med den generelle form.
 i, er kvadratisk, sætter standardformen alt til nul. Huske på, at
i, er kvadratisk, sætter standardformen alt til nul. Huske på, at  er koefficienter, der kan være et hvilket som helst heltal, så nu kan du ikke udfylde tal for variablerne - vi vil arbejde med den generelle form.
er koefficienter, der kan være et hvilket som helst heltal, så nu kan du ikke udfylde tal for variablerne - vi vil arbejde med den generelle form. - Den eneste betingelse er det
, ellers forenkles ligningen til en lineær ligning. Se om du kan finde generelle løsninger til særlige tilfælde, hvor
og
.
2. trække c  væk fra begge sider. Vores mål er at isolere
væk fra begge sider. Vores mål er at isolere  . Vi starter med at flytte en af koefficienterne til den anden side, så venstre side kun består af led med
. Vi starter med at flytte en af koefficienterne til den anden side, så venstre side kun består af led med  .
.
 væk fra begge sider. Vores mål er at isolere
væk fra begge sider. Vores mål er at isolere  . Vi starter med at flytte en af koefficienterne til den anden side, så venstre side kun består af led med
. Vi starter med at flytte en af koefficienterne til den anden side, så venstre side kun består af led med  .
.
3. Del begge sider -en  . Bemærk, at vi kunne have byttet disse i det forrige trin og stadig få det samme svar. Husk at dividere et polynomium med noget indebærer at dividere hvert af dets individuelle led. Dette gør det nemmere at opdele kvadratet.
. Bemærk, at vi kunne have byttet disse i det forrige trin og stadig få det samme svar. Husk at dividere et polynomium med noget indebærer at dividere hvert af dets individuelle led. Dette gør det nemmere at opdele kvadratet.
 . Bemærk, at vi kunne have byttet disse i det forrige trin og stadig få det samme svar. Husk at dividere et polynomium med noget indebærer at dividere hvert af dets individuelle led. Dette gør det nemmere at opdele kvadratet.
. Bemærk, at vi kunne have byttet disse i det forrige trin og stadig få det samme svar. Husk at dividere et polynomium med noget indebærer at dividere hvert af dets individuelle led. Dette gør det nemmere at opdele kvadratet.
4.Del firkanten. Husk at målet er at skabe et udtryk  at omskrive som
at omskrive som  hvorved
hvorved  er en koefficient. Dette er muligvis ikke umiddelbart klart for dig. For at gøre det klarere, omskriv
er en koefficient. Dette er muligvis ikke umiddelbart klart for dig. For at gøre det klarere, omskriv  hvis
hvis  ved at gange udtrykket med
ved at gange udtrykket med  Vi kan gøre dette, fordi gange med 1 ikke ændrer noget. Det kan vi nu tydeligt se i vores tilfælde
Vi kan gøre dette, fordi gange med 1 ikke ændrer noget. Det kan vi nu tydeligt se i vores tilfælde  , så kun udtrykket mangler
, så kun udtrykket mangler  . For at opdele kvadratet tilføjer vi det således på begge sider – nemlig,
. For at opdele kvadratet tilføjer vi det således på begge sider – nemlig,  Og så kan vi selvfølgelig faktorisere.
Og så kan vi selvfølgelig faktorisere.
 at omskrive som
at omskrive som  hvorved
hvorved  er en koefficient. Dette er muligvis ikke umiddelbart klart for dig. For at gøre det klarere, omskriv
er en koefficient. Dette er muligvis ikke umiddelbart klart for dig. For at gøre det klarere, omskriv  hvis
hvis  ved at gange udtrykket med
ved at gange udtrykket med  Vi kan gøre dette, fordi gange med 1 ikke ændrer noget. Det kan vi nu tydeligt se i vores tilfælde
Vi kan gøre dette, fordi gange med 1 ikke ændrer noget. Det kan vi nu tydeligt se i vores tilfælde  , så kun udtrykket mangler
, så kun udtrykket mangler  . For at opdele kvadratet tilføjer vi det således på begge sider – nemlig,
. For at opdele kvadratet tilføjer vi det således på begge sider – nemlig,  Og så kan vi selvfølgelig faktorisere.
Og så kan vi selvfølgelig faktorisere.
 , fordi
, fordi  er i nævneren, og du kan ikke dividere med nul.
er i nævneren, og du kan ikke dividere med nul.5. Skriv højre side under en fællesnævner. Vi ønsker, at begge nævnere skal være  er, så gange udtrykket
er, så gange udtrykket  af
af  .
.
 er, så gange udtrykket
er, så gange udtrykket  af
af  .
.
6. Beregn kvadratroden af begge sider. Det er dog vigtigt, at du forstår, at du ved at gøre dette grundlæggende tager to trin. Når du tager kvadratroden af  , så får du
, så får du  ikke. Du får dybest set den absolutte værdi af det,
ikke. Du får dybest set den absolutte værdi af det,  . Denne absolutte værdi er vigtig for at få begge rødder - blot at placere kvadratrødder over begge sider vil kun give en af rødderne.
. Denne absolutte værdi er vigtig for at få begge rødder - blot at placere kvadratrødder over begge sider vil kun give en af rødderne.
 , så får du
, så får du  ikke. Du får dybest set den absolutte værdi af det,
ikke. Du får dybest set den absolutte værdi af det,  . Denne absolutte værdi er vigtig for at få begge rødder - blot at placere kvadratrødder over begge sider vil kun give en af rødderne.
. Denne absolutte værdi er vigtig for at få begge rødder - blot at placere kvadratrødder over begge sider vil kun give en af rødderne.
 at placere til højre. Vi kan gøre dette, fordi den absolutte værdi ikke skelner mellem positive og negative tal, så de er begge gyldige. Denne detalje er grunden til, at andengradsligningen gør det muligt at få to rødder som et resultat.
at placere til højre. Vi kan gøre dette, fordi den absolutte værdi ikke skelner mellem positive og negative tal, så de er begge gyldige. Denne detalje er grunden til, at andengradsligningen gør det muligt at få to rødder som et resultat.
 Så kan vi tage kvadratroden af nævneren.
Så kan vi tage kvadratroden af nævneren.
7. isolere x  ved at trække fra
ved at trække fra b 2 -en  på begge sider.
på begge sider.
 ved at trække fra
ved at trække fra  på begge sider.
på begge sider.
8. Skriv højre side under en fællesnævner. Dette er ikke som abc-formlen, formlen til at løse en andengradsligning i standardform. Dette virker for enhver  og giver
og giver  som et resultat, som kan være et reelt eller komplekst tal. For at bekræfte, at denne proces fungerer, skal du blot følge trinene i denne artikel i omvendt rækkefølge for at vende tilbage til standardformularen.
som et resultat, som kan være et reelt eller komplekst tal. For at bekræfte, at denne proces fungerer, skal du blot følge trinene i denne artikel i omvendt rækkefølge for at vende tilbage til standardformularen.
 og giver
og giver  som et resultat, som kan være et reelt eller komplekst tal. For at bekræfte, at denne proces fungerer, skal du blot følge trinene i denne artikel i omvendt rækkefølge for at vende tilbage til standardformularen.
som et resultat, som kan være et reelt eller komplekst tal. For at bekræfte, at denne proces fungerer, skal du blot følge trinene i denne artikel i omvendt rækkefølge for at vende tilbage til standardformularen.
Tips
- Det er interessant at bemærke, at abc-formlen også gælder for komplekse koefficienter, selvom du skal forenkle en smule mere for at få det endelige svar, og rødderne er ikke konjugerede par. Problemer med kvadratiske udtryk er dog næsten altid givet med reelle koefficienter.
Artikler om emnet "Lær kvadratinddeling"
Оцените, пожалуйста статью
Populær