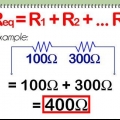
For eksempel har et seriekredsløb en modstand på 2 Ω (ohm), 5 Ω og 7 Ω. Kredsløbets samlede modstand er 2 + 5 + 7 = 14 Ω. 
Strømmen af et seriekredsløb er den samme på alle punkter i kredsløbet. Hvis du ved, hvad strømmen er på et bestemt punkt, kan du bruge denne værdi i ligningen. Den samlede spænding er lig med spændingen på strømforsyningen (batteriet). det er ikke lig med spændingen over en komponent. 
For eksempel er et seriekredsløb drevet af et 12 volt batteri, og strømmen er lig med 8 ampere. Den samlede modstand over kredsløbet er da Rt = 12 volt / 8 ampere = 1,5 ohm. 

For eksempel har et parallelkredsløb tre grene med modstande 10 Ω, 2 Ω og 1 Ω.
Brug formlen og løs for Rt:
og løs for Rt:
Konverter brøker til fællesnævneren:

Gang begge sider med Rt: 1 = 1.6Rt
Rt = 1/1.6 = 0.625 Ω. 
I et parallelkredsløb er spændingen over en gren lig med den samlede spænding over kredsløbet. Så længe du kender spændingen over en gren, kan du fortsætte. Den samlede spænding er også lig med spændingen af kredsløbets strømkilde, såsom et batteri. I et parallelkredsløb kan strømmen over hver gren være forskellig. du har i alt kræver strøm, ellers kan man ikke finde ud af, hvad den samlede modstand er. 
For eksempel har et parallelkredsløb en spænding på 9 volt og en strøm på 3 ampere. Den samlede modstand Rt = 9 volt / 3 ampere = 3. 
I praktiske applikationer betyder dette normalt, at en modstand har svigtet eller er forbigået (kortsluttet), hvilket tillader den højere strøm at beskadige andre dele af kredsløbet. 

Eksempelkredsløbet har to grene med modstand R1 = 5 Ω og R2 = 3.


 Ω
Ω 
I eksemplet ovenfor kan du ignorere de to grene og betragte dem som én modstand på 1,875 Ω. 
Det forenklede diagram har en 1 Ω modstand, 1.5 Ω modstand, og sektionen på 1,875 Ω, du lige har beregnet. Disse er alle forbundet i serie, så  Ω.
Ω. 


P = VI (effekt = spænding x strøm) Ohms lov fortæller os, at V = IR. Erstat IR med V i den første formel: P = (IR)I = IR. Omarranger for at bestemme modstand: R = P / I. I et seriekredsløb er strømmen over en komponent den samme som den samlede strøm. Dette gælder ikke for et parallelkredsløb. 
P = VI Omarranger Ohms lov til I: I = V / R. Erstat V/R med I i potensformlen: P = V(V/R) = V/R. Omarranger formlen for at løse for modstand: R = V/P. I et parallelkredsløb er spændingen over en gren den samme som den samlede spænding. Dette gælder ikke for et seriekredsløb: spændingen over en komponent er ikke lig med den samlede spænding.
Beregning af den samlede modstand i et kredsløb
Indhold
Der er to måder at forbinde elektriske komponenter på. Seriekredsløb er komponenter, der er forbundet efter hinanden, mens komponenter i et parallelkredsløb er forbundet i parallelle forgreninger. Den måde, modstande er koblet på, bestemmer, hvordan de bidrager til kredsløbets samlede modstand.
Trin
Metode 1 af 4: Serieforbindelse

1. Lær at genkende et seriekredsløb. Et seriekredsløb er en enkelt sløjfe uden forgreninger. Alle modstande eller andre komponenter er arrangeret i rækkefølge.

2. Læg alle modstandene sammen. I et seriekredsløb er den samlede modstand lig med summen af alle modstande. Den samme strøm løber gennem hver modstand, så hver modstand opfører sig som forventet.

3. Start med strømstyrken og spændingen i stedet for. Hvis du ikke ved, hvad de individuelle modstandsværdier er, kan du beregne dem ved hjælp af Ohms lov: V = IR eller spænding = strøm x modstand. Det første trin er at bestemme strømmen i kredsløbet og den samlede spænding:

4. Brug disse værdier i Ohms lov. Omarranger V = IR for at løse modstanden: R = V / I (modstand = spænding / strøm). Anvend værdierne fundet på denne formel for at få den samlede modstand.
Metode 2 af 4: Parallel kredsløb

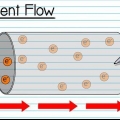
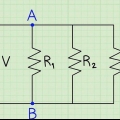
1. Forstå hvad parallelle kredsløb er. Et parallelt kredsløb forgrener sig i flere stier, som derefter konvergerer igen. Strøm løber gennem hver gren af kredsløbet.
- Hvis kredsløbet har modstande på hovedgrenen (før eller efter grenen), eller hvis der er to eller flere modstande på en gren, skal du springe til instruktionerne for et kombineret kredsløb.

2. Beregn den samlede modstand af modstanden i hver gren. Da hver modstand kun bremser strømmen, der passerer gennem en gren, har den kun en lille effekt på kredsløbets samlede modstand. Formlen for den samlede modstand Rt er  , hvor R1 modstanden er af den første gren, R2 modstanden af den anden gren, og så videre, til den sidste gren Rn.
, hvor R1 modstanden er af den første gren, R2 modstanden af den anden gren, og så videre, til den sidste gren Rn.
 , hvor R1 modstanden er af den første gren, R2 modstanden af den anden gren, og så videre, til den sidste gren Rn.
, hvor R1 modstanden er af den første gren, R2 modstanden af den anden gren, og så videre, til den sidste gren Rn.Brug formlen
 og løs for Rt:
og løs for Rt:Konverter brøker til fællesnævneren:


Gang begge sider med Rt: 1 = 1.6Rt
Rt = 1/1.6 = 0.625 Ω.

3. Start med den samlede strøm og spænding i stedet for. Hvis du ikke kender værdien af de enkelte modstande, skal du bruge værdien af strøm og spænding:

4. Brug disse værdier i Ohms lov. Hvis du kender den samlede strøm og spænding over hele kredsløbet, kan du finde den samlede modstand ved hjælp af Ohms lov: R = V / I.

5. Pas på grene med en modstand på nul. Hvis en gren af et parallelkredsløb ikke har nogen modstand, så løber al strøm gennem den gren. Kredsløbets modstand er da nul ohm.
Metode 3 af 4: Kombineret kredsløb

1. Opdel dit kredsløb i seriekredsløb og parallelkredsløb. Et kombineret kredsløb har et antal komponenter forbundet i serie (den ene efter den anden), og andre komponenter forbundet parallelt (i forskellige grene). Se efter dele af dit diagram, der kan forenkles til et serie- eller parallelkredsløb. Sæt en cirkel om hver af disse brikker for at hjælpe dig med at huske dem.
- For eksempel har et kredsløb en 1 modstand og en 1,5 Ω modstand forbundet i serie. Efter den anden modstand opdeles kredsløbet i to parallelle grene, den ene med en 5 modstand og den anden med en 3 Ω modstand.
Sæt en cirkel rundt om de to parallelle grene for at skelne dem fra resten af kredsløbet.

2. Find modstanden af hver parallel sektion. Brug formlen for parallel modstand  at finde den samlede modstand af en enkelt parallel sektion af kredsløbet.
at finde den samlede modstand af en enkelt parallel sektion af kredsløbet.
 at finde den samlede modstand af en enkelt parallel sektion af kredsløbet.
at finde den samlede modstand af en enkelt parallel sektion af kredsløbet.

 Ω
Ω
3. Forenkle dit diagram. Når du har fundet den samlede modstand af en parallel sektion, kan du krydse hele sektionen ud i dit diagram. Behandl den sektion som en enkelt ledning med en modstand svarende til den værdi, du fandt.

4. Tilføj seriemodstandene sammen. Når du har udskiftet hvert parallelkredsløb med en enkelt modstand, skal dit diagram være en enkelt sløjfe: et seriekredsløb. Den samlede modstand i et seriekredsløb er lig med summen af alle individuelle modstande, så læg dem bare sammen for at få svaret.
 Ω.
Ω.
5. Brug Ohms lov til at finde de ukendte værdier. Hvis du ikke ved, hvad modstanden er i en bestemt komponent af dit kredsløb, så se efter en måde at beregne det alligevel. Hvis du kender spændingen V og strømmen I over den komponent, skal du bestemme dens modstand ved hjælp af Ohms lov: R = V / I.
Metode 4 af 4: Formler med kraft

1. Lær formlen for magt. Strøm er den grad, hvori kredsløbet forbruger energi, og i hvilken grad det leverer energi til den strøm, der driver kredsløbet (såsom en lampe). Den samlede effekt af et kredsløb er lig med produktet af den samlede spænding og den samlede strøm. Eller i form af en ligning: P = VI.
- Husk, at når du løser dette for den samlede modstand, har du brug for den samlede effekt af kredsløbet. Det er ikke nok bare at kende den effekt, der passerer gennem én komponent.

2. Bestem modstand ved hjælp af strøm og strøm. Når du kender disse værdier, kan du kombinere de to formler for at bestemme modstanden:

3. Bestem modstand ved hjælp af strøm og spænding. Hvis du kun kender effekt og spænding, kan du bruge samme tilgang til at bestemme modstanden. Husk at bruge den fulde spænding over kredsløbet eller spændingen fra batteriet, der driver kredsløbet:
Tips
- Effekten måles i watt (W).
- Spænding måles i volt (V).
- Strøm måles i ampere (A) eller i milliampere (mA). 1 man =
A = 0,001 A.
- Potensen P som brugt i disse formler refererer til det direkte mål for effekten på et bestemt tidspunkt. Hvis kredsløbet bruger vekselstrøm (AC), ændres effekten kontinuerligt. Elektrikere beregner den gennemsnitlige effekt af AC-kredsløb ved hjælp af formlen Pgennemsnit = VIcosθ, hvor cosθ er kredsløbets effektfaktor.
Artikler om emnet "Beregning af den samlede modstand i et kredsløb"
Оцените, пожалуйста статью
Populær