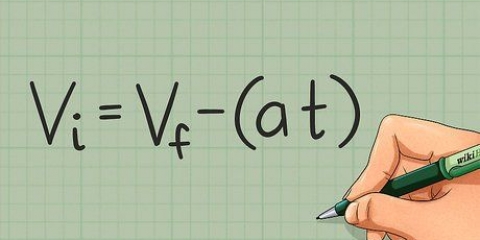Sådan bestemmes nøjagtighed

Indhold

Trin
Tips

Nøjagtighed betyder, at en måling med et bestemt værktøj eller instrument giver lignende resultater, hver gang det bruges. For eksempel, hvis du træder på en vægt fem gange i træk, skal en præcis vægt vise dig den samme vægt hver gang. I matematik og naturvidenskab er beregningsnøjagtighed afgørende for at afgøre, om dine instrumenter og målinger er gode nok til at få gode data. Du kan repræsentere nøjagtigheden af hvert datasæt ved hjælp af værdiintervallet, middelafvigelsen eller standardafvigelsen.

Trin

Metode 1 af 4: Beregning af rækkevidden

1. Bestem den højeste målte værdi. Det hjælper at begynde at sortere dine data i numerisk rækkefølge, fra laveste til højeste. Dette sikrer, at du ikke springer nogen af værdierne over. Vælg derefter værdien i slutningen af listen.

Sig for eksempel, at du tester nøjagtigheden af en skala og ser fem aflæsninger: 11, 13, 12, 14, 12. Sorteret er disse værdier vist som 11, 12, 12, 13, 14. Den højeste værdi er 14.

Billede med titlen Calculate Precision Step 2

2. Bestem den laveste målte værdi. Når dine data er sorteret, er det lige så nemt at finde den laveste værdi som at se i begyndelsen af listen.

Inden for måledataene på skalaen er den laveste værdi 11.

Billede med titlen Beregn præcision Trin 3

3. Træk den laveste værdi fra den højeste. Rækkevidden af et sæt data er forskellen mellem de højeste og laveste aflæsninger. Træk bare fra hinanden. Algebraisk er intervallet udtrykt som:

rækkevidde = x (m -en x) - x (m jeg n)

${tekst{Range}}=x(max)-x(min)$

Rækkevidden af prøvedataene er:

rækkevidde = x (m -en x) - x (m jeg n) = 14 - 11 = 3

${tekst{Range}}=x(max)-x(min)=14-11=3$

Billede med titlen Beregn præcision Trin 4

4. Vis området som nøjagtigheden. Ved indberetning af data er det vigtigt, at læserne ved, hvad du har målt. Fordi nøjagtighed kommer i forskellige metrics, skal du angive, hvad du vil rapportere. For disse data angiver du: middel = 12,4, interval = 3. Eller ganske enkelt: middel = 12,4 ±3.

Middelværdien er ikke nødvendigvis en del af beregning af rækkevidde eller nøjagtighed, men er generelt den første beregning til rapportering af den målte værdi. Middelværdien opnås ved at dividere summen af de målte værdier med antallet af emner i gruppen. Middelværdien af denne dataserie er (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Metode 2 af 4: Beregning af middel afvigelse

Billede med titlen Calculate Precision Step 5

1. Bestem først gennemsnittet af dataene. Middelafvigelsen er et mere detaljeret mål for præcisionen af en gruppe målinger eller værdier af et eksperiment. Det første trin i at finde middelafvigelsen er at beregne middelværdien af de målte værdier. Middelværdien er summen af værdierne divideret med antallet af målinger.

I dette eksempel bruger vi de samme eksempeldata som før. Antag, at der er foretaget fem målinger, 11, 12, 13, 14 og 12. Middelværdien af disse værdier er (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Billede med titlen Calculate Precision Step 6

2. Beregn den absolutte afvigelse af hver værdi fra middelværdien. Til denne beregning af præcision skal du bestemme, hvor tæt hver værdi er på middelværdien. For at gøre dette skal du trække gennemsnittet af hvert tal fra. For denne måling er det lige meget, om værdien er over eller under gennemsnittet. Træk tallene fra og brug blot den positive værdi af resultatet. Dette er også kendt som `absolut værdi`.

Algebraisk er den absolutte værdi repræsenteret ved at placere to lodrette streger rundt om beregningen. Som følger:

Absolut afvigelse = | x - μ |

${text{Absolut afvigelse}}=|x-mu |$

Dette regnestykke siger

x

$x$ for hver af de eksperimentelle værdier og

μ

$mu$ for det beregnede gennemsnit.

Hvad angår værdierne af prøvedataserien, er de absolutte afvigelser:

| 12 - 12, 4 | = 0, 4

$|12-12,4|=0,4$

| 11 - 12, 4 | = 1, 4

$|11-12,4|=1,4$

| 14 - 12, 4 | = 1, 6

$|14-12,4|=1,6$

| 13 - 12, 4 | = 0, 6

$|13-12,4|=0,6$

| 12 - 12, 4 | = 0, 4

$|12-12,4|=0,4$

Billede med titlen Calculate Precision Step 7

3. Bestem den gennemsnitlige afvigelse. Brug de absolutte afvigelser og find deres middelværdi. Som med det originale datasæt, lægger du værdierne sammen og dividerer summen med antallet af værdier. Dette er repræsenteret algebraisk som:

Gennemsnitlig afvigelse = Σ | x - μ | n

${text{Mean Deviation}}={frac{Sigma |x-mu |}{n}}$

Hvad angår disse eksempeldata, går beregningen sådan her:

Gennemsnitlig afvigelse = 0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4 5

${text{Mean deviation}}={frac{0.4+1.4+1.6+0.6+0.4}{5}}$

Gennemsnitlig afvigelse = 4, 4 5

${text{Gennemsnitsafvigelse}}={frac{4,4}{5}}$

Gennemsnitlig afvigelse = 0, 88

${text{Middelafvigelse}}=0,88$

Billede med titlen Calculate Precision Step 8

4. Angiv resultatet af nøjagtigheden. Dette resultat kan rapporteres som middelværdien plus eller minus middelafvigelsen. For dette eksempeldatasæt ser dette ud som 12,4 ±0,88. Bemærk, at angivelsen af nøjagtigheden som middelafvigelsen får målingen til at fremstå meget mere nøjagtig end med området.

Metode 3 af 4: Beregn standardafvigelsen

Billede med titlen Calculate Precision Step 9

1. Brug den korrekte formel for standardafvigelsen. For enhver datasætstørrelse er standardafvigelsen en pålidelig statistik til visning af præcision. Der er to formler til beregning af standardafvigelsen, med en meget lille forskel mellem dem. Du bruger én formel, hvis dine metrics dækker en hel population. Den anden formel bruges, hvis de målte data kun er et udsnit af populationen.

Dine data repræsenterer en hel population, hvis du har indsamlet alle mulige mål fra alle mulige emner. For eksempel, hvis du tester mennesker med en meget sjælden sygdom, og du er sikker på, at du har testet alle med denne sygdom, omfatter dette hele befolkningen. Formlen for standardafvigelsen er i dette tilfælde:

$Σ = \sqrt{} Σ (x - μ) 2 n$ $sigma ={sqrt{{frac{Sigma (x-mu )^{2}}{n}}}}$

En stikprøve er en gruppe af data, der er mindre end en hel population. Du vil normalt bruge denne mest. Standardafvigelsesformlen for en prøve er:

Σ = \sqrt{} Σ (x - μ) 2 n - 1

$sigma ={sqrt{{frac{Sigma (x-mu )^{2}}{n-1}}}}$

Bemærk, at den eneste forskel er brøkens nævner. For en fuld befolkning divideres med

n

$n$ . Hvis du har en prøve, så del gerne

n - 1

$n-1$ .

Billede med titlen Calculate Precision Step 10

2. Find gennemsnittet af dataværdierne. Ligesom ved beregningen af middelafvigelsen starter man med at bestemme middelværdien af dataværdierne.

Ved at bruge det samme sæt af aflæsninger som nævnt ovenfor, er middelværdien 12,4.

Billede med titlen Calculate Precision Step 11

3. Find kvadratet af hver variant. For hvert datapunkt skal du trække dataværdien fra middelværdien og kvadrere resultatet. Da du kvadrerer disse variationer, er det lige meget, om forskellen er positiv eller negativ. Kvadraten af forskellen er altid positiv.

For de fem dataværdier i dette eksempel går disse beregninger sådan her:

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

(11 - 12, 4) 2 = (- 1, 4)^{2} = 1, 96

$(11-12,4)^{2}=(-1,4)^{2}=1,96$

(14 - 12, 4) 2 = 1, 6^{2} = 2, 56

$(14-12,4)^{2}=1,6^{2}=2,56$

(13 - 12, 4) 2 = 0, 6^{2} = 0, 36

$(13-12,4)^{2}=0,6^{2}=0,36$

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

Billede med titlen Calculate Precision Step 12

4. Beregn summen af de kvadrerede forskelle. Tælleren for brøken i standardafvigelsen er summen af de kvadrerede forskelle mellem værdierne og middelværdien. Du kan bestemme dette beløb ved at lægge tallene fra den tidligere udregning sammen.

For eksempeldatasættet er disse:

0, 16 + 1, 96 + 2, 56 + 0, 36 + 0, 16 = 5, 2

$0,16+1,96+2,56+0,36+0,16=5,2$

Billede med titlen Calculate Precision Step 13

5. Divider efter datastørrelse. Dette er det eneste trin, der er anderledes i en populationsberegning sammenlignet med en stikprøve. For en komplet population dividerer du med

n

$n$ (antallet af værdier). I en prøve dividerer man med

n - 1

$n-1$ .

Følgende eksempel har kun fem målinger og er derfor kun en prøve. Så for de fem anvendte værdier skal du dividere med (5 - 1) eller 4. Resultatet er

5, 2 / 4 = 1, 3

$5,2/4=1,3$ .

Billede med titlen Calculate Precision Step 14

6. Find kvadratroden af resultatet. På dette tidspunkt repræsenterer beregningen det, der kaldes variansen af datasættet. Standardafvigelsen er kvadratroden af variansen. Brug en lommeregner til at finde kvadratroden og dermed standardafvigelsen.

Σ = \sqrt{1.3} = 1, 14

$sigma ={sqrt{1.3}}=1,14$

Billede med titlen Calculate Precision Step 15

7. Vis dit resultat. Ved hjælp af denne beregning kan præcisionen af skalaen angives ved at angive middelværdien plus eller minus standardafvigelsen. For disse data bliver det 12,4 ±1,14.

Standardafvigelsen er måske det mest almindelige mål for præcision. Men for klarhedens skyld er det stadig en god idé at bruge en fodnote eller parenteser til at angive, at præcisionsværdien repræsenterer standardafvigelsen.

Metode 4 af 4: Beslut, hvordan du angiver nøjagtighed

Billede med titlen Calculate Precision Step 16

1. Brug ordet nøjagtighed korrekt. Nøjagtighed er et udtryk, der bruges til at angive gentageligheden af målinger. Hvis du indsamler en gruppe data, enten ved måling eller gennem et bestemt eksperiment, beskriver nøjagtigheden, hvor tæt resultaterne af hver måling eller eksperiment vil være.

Nøjagtighed er ikke det samme som nøjagtighed. Nøjagtighed måler, hvor tæt eksperimentelle værdier er på den faktiske eller teoretiske værdi, mens nøjagtighed måler, hvor tæt de målte værdier er på hinanden.
Data kan være nøjagtige, men ikke nøjagtige eller nøjagtige, men ikke nøjagtige. Nøjagtige aflæsninger kan være tæt på målet, men er muligvis ikke tæt på hinanden. Nøjagtige aflæsninger er tæt på hinanden, uanset om de er tæt på målværdierne eller ej.

Billede med titlen Calculate Precision Step 17

2. Vælg den bedste grad af nøjagtighed. Ordet `nøjagtighed` har ikke en enkelt betydning. Det er muligt at vise nøjagtighed med flere forskellige målinger. Du bliver nødt til at beslutte, hvilken der er den bedste.

Rækkevidde. For små datasæt med omkring ti eller færre målinger er værdiintervallet et godt mål for nøjagtighed. Dette gælder især, hvis værdierne er grupperet ret tæt sammen. Hvis du opdager, at en eller to værdier er langt fra de andre værdier, så skal du nok bruge en anden beregning.

Gennemsnitlig afvigelse. Den gennemsnitlige afvigelse er et mere nøjagtigt mål for nøjagtigheden af et lille sæt dataværdier.

standardafvigelse. Standardafvigelsen er måske det mest anerkendte mål for nøjagtighed. Standardafvigelse kan bruges til at beregne nøjagtigheden af målingerne for en hel population eller en stikprøve af populationen.

Billede med titlen Calculate Precision Step 18

3. Giv en klar fremstilling af dine resultater. Meget ofte vil forskere rapportere data ved at angive middelværdien af den målte værdi efterfulgt af graden af nøjagtighed. Nøjagtigheden vises med `±`-symbolet. Dette giver en indikation af nøjagtighed, men det forklarer ikke klart for læseren, om tallet efter `±`-symbolet er et område, standardafvigelse eller en anden måling. For at angive dette tydeligt, skal du definere hvilket niveau af nøjagtighed du har brugt, enten i en fodnote eller som en kommentar i parentes.

For en given dataserie kan resultatet blive vist som 12,4 ±3. En mere beskrivende måde at angive de samme data på ville dog være denne: `Middelværdi = 12,4, Interval = 3.`

Tips

Hvis en af værdierne i prøven er meget højere eller lavere end resten af dine værdier, skal du ikke udelukke denne værdi fra dine beregninger. Selvom det var en fejl, forbliver det data og skal bruges til korrekt beregning.
Kun fem værdier blev brugt i denne artikel for matematisk enkelhed. I et egentligt eksperiment bør du bruge mere end fem metrics til en mere nøjagtig beregning. Jo flere prøver du kører, jo mere nøjagtige.