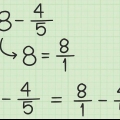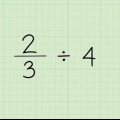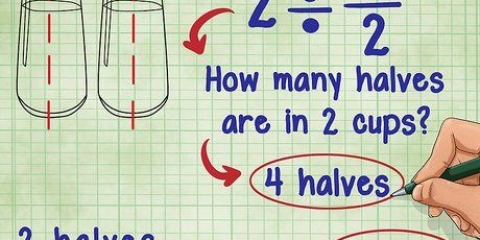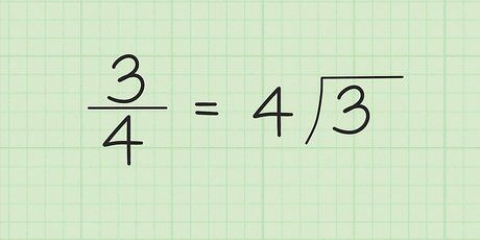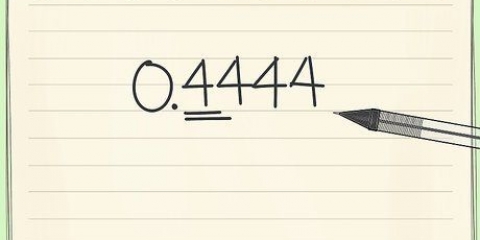For eksempel: det omvendte (det omvendte) af  er
er  .
. 
For eksempel: 

For eksempel:  kan forenkles til det blandede antal
kan forenkles til det blandede antal  .
. 

For eksempel hvis du dividerer med  , så angiver 4`eren i nævneren, at du skal dele helheden i fire lige store dele.
, så angiver 4`eren i nævneren, at du skal dele helheden i fire lige store dele. 
For eksempel: forestil dig del 5  , så farver du tre fjerdedele i en anden farve for hver gruppe. Bemærk, at mange grupper vil indeholde to kvartaler i en helhed og en fjerdedel i en anden helhed.
, så farver du tre fjerdedele i en anden farve for hver gruppe. Bemærk, at mange grupper vil indeholde to kvartaler i en helhed og en fjerdedel i en anden helhed. 
For eksempel havde du seks grupper af  skal lave de fem cirkler.
skal lave de fem cirkler. 
For eksempel: efter at have opdelt de fem figurer i grupper af  , har du to kvarter, eller
, har du to kvarter, eller  om. Da en hel gruppe består af tre stykker, og du har to stykker, er din brøk
om. Da en hel gruppe består af tre stykker, og du har to stykker, er din brøk  .
. 
For eksempel:  .
. 

Lav en brøkdel af 16 ved at gøre den til en tæller med nævneren 1:  .
. Find brøkens reciprokke ved at vende tæller og nævner om:  bliver til
bliver til  .
. Gang de to brøker sammen:  .
. Forenkle om nødvendigt:  .
. 
Tegn ni cirkler for at repræsentere de ni dåser. Fordi hun  spis ad gangen, del hver cirkel i tredjedele.
spis ad gangen, del hver cirkel i tredjedele. Farv grupperne af  .
. Tæl antallet af komplette grupper. Dette skal være 13. Fortolk de resterende stykker. Der er et stykke tilbage, og det er  . Fordi en hel gruppe
. Fordi en hel gruppe  er, du har en halv gruppe tilbage. Så brøkdelen er
er, du har en halv gruppe tilbage. Så brøkdelen er  .
. Kombiner antallet af grupper af heltal og brøker for at finde dit endelige svar:  .
.
At dividere et heltal med en brøk
Indhold
Hvis man vil dividere et helt tal med en brøk, regner man faktisk ud, hvor mange `grupper` af brøken der går ind i helheden. Standardmetoden til at dividere et helt tal med en brøk er at gange hele tallet med det reciproke af brøken. Du kan også oprette et diagram for at hjælpe med at visualisere denne beregning.
Trin
Metode 1 af 3: Gang med det omvendte

1. Konverter hele tallet til en brøk. Det gør du ved at lave hele tallet om til tælleren for en brøk. Lav nævneren 1.
- For eksempel: Beregn din
, så skifter du først
i
.

2. Find det reciproke af brøken. Den reciproke af et tal er lig med det omvendte af dette tal. For at finde den reciproke af en brøk, skift tæller og nævner.
 er
er  .
.
3. Gang de to brøker. For at gange brøker skal du først gange tællerne sammen. Gang derefter nævnerne sammen. Produktet af de to brøker er lig med kvotienten af dit oprindelige divisionsproblem.


4. Forenkle, hvis det er nødvendigt. Hvis du har en uægte brøk (dvs. tælleren er større end nævneren), kan problemet bede dig om at ændre det til et blandet tal. Normalt vil erklæringen bede om for at forenkle brøker til de laveste vilkår.
 kan forenkles til det blandede antal
kan forenkles til det blandede antal  .
.Metode 2 af 3: Tegning af et diagram

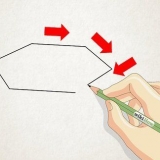
1. Tegn figurer, der repræsenterer hele tallet. Din form skal kunne opdeles i lige store grupper, fx en firkant eller en cirkel. Tegn formerne så store, at du kan dele dem i mindre stykker.
- For eksempel: i beregningen
, vil du tegne fem cirkler.

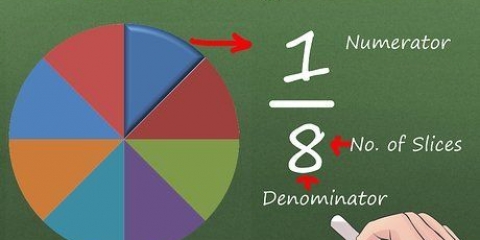
2. Divider hver hel form med nævneren af brøken. Nævneren af en brøk fortæller dig, hvor mange dele en hel form er opdelt i. Opdel hver hel form i dens dele som angivet af brøken.
 , så angiver 4`eren i nævneren, at du skal dele helheden i fire lige store dele.
, så angiver 4`eren i nævneren, at du skal dele helheden i fire lige store dele.
3. Skygge for grupperne, der repræsenterer brøken. Da man dividerer hele tallet med brøken, ser man hvor mange grupper af brøken der er i hele tallet. Så først angiver du grupperne. Det kan være nyttigt at give hver gruppe en anden farve, da nogle grupper har dele i to forskellige helformer. Lad de resterende stykker være tomme.
 , så farver du tre fjerdedele i en anden farve for hver gruppe. Bemærk, at mange grupper vil indeholde to kvartaler i en helhed og en fjerdedel i en anden helhed.
, så farver du tre fjerdedele i en anden farve for hver gruppe. Bemærk, at mange grupper vil indeholde to kvartaler i en helhed og en fjerdedel i en anden helhed.
4. Tæl antallet af hele grupper. Dette vil give dig hele tallet for dit svar.
 skal lave de fem cirkler.
skal lave de fem cirkler.
5. Fortolk de resterende stykker. Sammenlign antallet af stykker du har tilbage med en hel gruppe. Den brøkdel af en gruppe, du har tilbage, angiver brøkdelen af dit svar. Pas på ikke at sammenligne antallet af stykker du har med antallet af stykker du har med en hel form, da dette vil give dig den forkerte brøk.
 , har du to kvarter, eller
, har du to kvarter, eller  om. Da en hel gruppe består af tre stykker, og du har to stykker, er din brøk
om. Da en hel gruppe består af tre stykker, og du har to stykker, er din brøk  .
.
6. Skriv svaret ned. Kombiner grupperne af det hele tal med grupperne af brøken for at finde kvotienten af din oprindelige divisionssum.
 .
.Metode 3 af 3: Prøveproblemer med løsninger

1. Løse: Hvor ofte gør  i
i  ?
?
 i
i  ?
? - Fordi opgaven spørger, hvor mange grupper af
går i 8 er det en divisionssum.
- Lav en brøkdel af 8 ved at gøre den til en tæller med nævner 1:
.
- Find brøkens reciprokke ved at vende tæller og nævner om:
bliver til
.
- Gang de to brøker sammen:
.
- Forenkle om nødvendigt:
.

2. Løse: .
.
 .
. .
. bliver til
bliver til  .
. .
. .
.
3. Løs følgende problem ved at tegne et diagram. Rufus har ni dåser bønner. Hun spiser hver dag  en dåse. Hvor mange dage har hun dåser?
en dåse. Hvor mange dage har hun dåser?
 en dåse. Hvor mange dage har hun dåser?
en dåse. Hvor mange dage har hun dåser? spis ad gangen, del hver cirkel i tredjedele.
spis ad gangen, del hver cirkel i tredjedele. .
. . Fordi en hel gruppe
. Fordi en hel gruppe  er, du har en halv gruppe tilbage. Så brøkdelen er
er, du har en halv gruppe tilbage. Så brøkdelen er  .
. .
.Artikler om emnet "At dividere et heltal med en brøk"
Оцените, пожалуйста статью
Populær