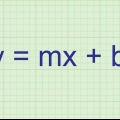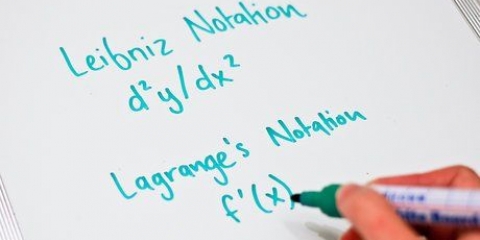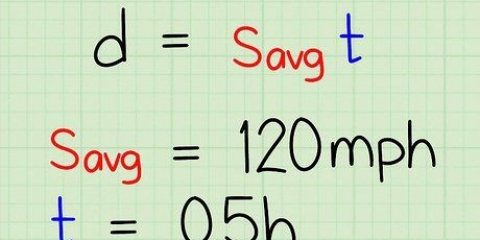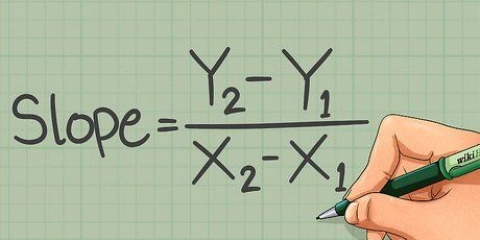Funktioner skrives ofte som  Det betyder, at funktionen
Det betyder, at funktionen  læg altid 3 til det tal du har for
læg altid 3 til det tal du har for  Udfyld. Hvis du indtaster 2, skriver du ned
Udfyld. Hvis du indtaster 2, skriver du ned  eller
eller 
Funktioner kan også vise komplekse bevægelser. NASA har for eksempel en funktion til at beskrive en rakets hastighed, baseret på brændstofforbrugsraten, vindmodstand og rakettens vægt. 

Grænser er nemmest at visualisere på en graf – for eksempel er der punkter, der er tæt på at røre en graf, men aldrig helt? Grænser kan være antal, uendelige eller endda ikke-eksisterende. For eksempel med additionssekvensen 1 + 2 + 2 + 2 + 2 + ... og dette fortsætter i det uendelige, så bliver det endelige tal uendeligt stort. Grænsen bliver så uendelig. 
Algebra. Du skal forstå de forskellige processer og kunne løse ligninger og ligningssystemer med flere variable. Forstå det grundlæggende i samlinger. Øv dig i at lave grafer. Geometri. Geometri er studiet af former. Du skal have den grundlæggende viden om trekanter, rektangler og cirkler, og hvordan man beregner ting som omkreds og areal. Forstå vinkler, linjer og koordinater trigonometri. Trigonometri er den gren af matematik, der beskæftiger sig med egenskaberne af cirkler og retvinklede trekanter. Vide, hvordan man bruger trigonometriske identiteter, grafer, funktioner og inverse trigonometriske funktioner. 
Mange smartphones og tablets tilbyder i dag billige, men effektive grafiske apps, hvis du ikke vil eller ikke kan købe en grafregner. 

Acceleration er en afledt - den fortæller dig, hvor hurtigt noget accelererer eller decelererer, dvs. hvordan dets hastighed ændrer sig. 
Hældningen af linjen er ændringen i y divideret med ændringen i x`.` Jo større hældning hældningen er, jo stejlere er linjen. Ændring af stejle linjer repræsenterer derfor en hurtig ændring. Opfrisk din viden om at bestemme hældningen af en linje, hvis den er sunket en smule. 
For eksempel i  du kan vælge to vilkårlige punkter og beregne hældningen. tage
du kan vælge to vilkårlige punkter og beregne hældningen. tage  og
og  Hældningen mellem disse punkter er da lig med
Hældningen mellem disse punkter er da lig med  Det betyder, at skiftet mellem
Det betyder, at skiftet mellem  og
og  er lig med 2.
er lig med 2. 
For eksempel undersøger forskere, hvor hurtigt nogle arter uddør for at redde dem. Men flere dyr dør om vinteren end om sommeren, så det er ikke nyttigt at studere ændringshastigheden over hele året - det er bedre at bestemme ændringshastigheden inden for en mindre periode, f.eks. fra 1. juli til 1. august. 
Tænk på eksemplet, hvor du bliver ved med at dividere 1 med 2, og med det 1/2, 1/4, 1/8 osv. får. Så i sidste ende kommer du tæt på nul, og svaret er `næsten nul`. Punkterne er så tæt på hinanden, at de er `næsten ens`. Dette er karakteren af derivater. 

Der er forskellige notationer for derivater. I det foregående trin blev derivater angivet med en indtegning – derivatet af  så skriv det ned som
så skriv det ned som  Dette kaldes Lagranges notation.
Dette kaldes Lagranges notation. Der er en anden måde, der ofte bruges til at skrive derivater. I stedet for med omhu, bemærker du  Husk at funktionen
Husk at funktionen  afhænger af variablen
afhænger af variablen  Så vi skriver den afledte som
Så vi skriver den afledte som  --- afledt af
--- afledt af  så længe
så længe Dette kaldes Leibniz .s notation.
Dette kaldes Leibniz .s notation. 
Hvor hurtigt bevæger marmoren sig?? Med hvilken hastighed ændres positionen (eller afledningen) af den bevægelige kugle?? Vi kalder denne afledte `hastighed`. Rul kuglen ned ad en rampe og se, hvordan hastigheden ændrer sig. Hvad er ændringshastigheden, eller afledt, af marmorens hastighed?? Denne afledte er det, vi kalder `acceleration`. Rul marmoren langs et bølgende spor, som en rutsjebane. Hvor meget tager kuglen fart, når den ruller ned, og hvor meget bremser kuglen op ad bakke?? Hvor hurtigt går marmoren præcis, når den er halvvejs op ad den første bakke? Dette er så den øjeblikkelige ændringshastighed, eller den afledte, af den marmor på det ene specifikke punkt. 




Antag, at du lægger en masse små segmenter sammen under grafen, og at bredden af hvert segment næsten nul er. 
Det første symbol,  er symbolet for integration (dette er faktisk et strakt S).
er symbolet for integration (dette er faktisk et strakt S). Anden del,  er funktionen. Hvis det er inde i integralet, kaldes det de integral.
er funktionen. Hvis det er inde i integralet, kaldes det de integral. Og til sidst  til sidst, som fortæller dig, hvilken variabel du integrerer og til hvad. Fordi funktionen
til sidst, som fortæller dig, hvilken variabel du integrerer og til hvad. Fordi funktionen  kommer an på
kommer an på  er det, du integrerer dig imod.
er det, du integrerer dig imod. Husk, at den variabel, du integrerer, ikke altid er det  vil være, så vær forsigtig med, hvad du skriver ned.
vil være, så vær forsigtig med, hvad du skriver ned. 
Integrer ved substitution. Beregning af ubestemte integraler. Integrer ved at dele. 
Husk f.eks., at den afledede af hastighed er acceleration, så du kan bruge hastighed til at finde acceleration. Men hvis du kun kender accelerationen af noget (som genstande, der falder på grund af tyngdekraften), kan du integrere for at finde hastigheden igen! 
Dette giver dig mulighed for at bestemme volumenet af ethvert fast stof, så længe du har en funktion, der repræsenterer det. For eksempel kan du oprette en funktion, der følger bunden af en sø, og så bruge den til at bestemme søens volumen, eller hvor meget vand den indeholder.
Forståelse af analyser
Indhold
Analyse (også kaldet calculus) er en gren af matematikken fokuseret på grænser, funktioner, afledte, integraler og uendelige rækker. Dette emne dækker meget af matematik og ligger til grund for mange af de formler og ligninger, der bruges i fysik og mekanik. Du skal formentlig have flere års matematik i gymnasiet for at forstå analyse ordentligt, men denne artikel vil få dig i gang med at genkende nøglebegreberne, samt en bedre forståelse af teorien.
Trin
Del 1 af 3: Det grundlæggende i analyse

1. Analyse er studiet af, hvordan tingene ændrer sig. Analyse er en gren af matematikken, der undersøger tal og grafer, normalt taget fra data fra den virkelige verden, og forklarer, hvordan de ændrer sig. Selvom dette måske ikke virker særlig nyttigt i starten, er analyse en af de mest brugte grene af matematik. Forestil dig at have værktøjerne, der kan fortælle dig, hvor hurtigt din virksomhed vokser til enhver tid, eller til at kortlægge et rumskibs kurs, og hvor hurtigt brændstoffet bliver brugt op. Analyse er et vigtigt værktøj inden for teknik, økonomi, statistik, kemi og fysik og har bidraget til mange opfindelser og opdagelser.

2. Funktioner er relationer mellem to tal og bruges til at kortlægge relationer. De er regler for forholdet mellem tal, og matematikere bruger dem til at lave grafer. I en funktion har hvert input nøjagtigt ét udfald. For eksempel: i  returnerer enhver værdi af
returnerer enhver værdi af  en ny værdi for
en ny værdi for  I tilfælde af at
I tilfælde af at  så er
så er  I tilfælde af at
I tilfælde af at  , derefter
, derefter  Analyse studerer altid funktioner, og hvordan de ændrer sig, ved at bruge disse funktioner til at kortlægge relationer.
Analyse studerer altid funktioner, og hvordan de ændrer sig, ved at bruge disse funktioner til at kortlægge relationer.
 returnerer enhver værdi af
returnerer enhver værdi af  en ny værdi for
en ny værdi for  I tilfælde af at
I tilfælde af at  så er
så er  I tilfælde af at
I tilfælde af at  , derefter
, derefter  Analyse studerer altid funktioner, og hvordan de ændrer sig, ved at bruge disse funktioner til at kortlægge relationer.
Analyse studerer altid funktioner, og hvordan de ændrer sig, ved at bruge disse funktioner til at kortlægge relationer. Det betyder, at funktionen
Det betyder, at funktionen  læg altid 3 til det tal du har for
læg altid 3 til det tal du har for  Udfyld. Hvis du indtaster 2, skriver du ned
Udfyld. Hvis du indtaster 2, skriver du ned  eller
eller 

3. Tænk på begrebet uendelighed. Uendelighed er den kontinuerlige gentagelse af en proces. Det er ikke et bestemt sted (du kan ikke gå til det uendelige), men snarere adfærden af et tal eller en ligning, hvis det gøres for evigt. Dette er vigtigt for at studere forandring: Du vil måske gerne vide, hvor hurtigt din bil bevæger sig på et givet tidspunkt, men er det, hvor hurtigt din bil bevæger sig i det aktuelle sekund?? millisekund? Nanosekund? Du kan finde uendeligt meget mindre bidder af tid for at være endnu mere præcis, og det er, når analysen starter.

4. Forstå begrebet grænser. En grænse fortæller dig, hvad der sker, når noget nærmer sig det uendelige. Tag tallet 1 og divider det med 2. Fortsæt med at dividere med 2, igen og igen. 1 bliver til ½ og derefter 1/4, 1/8, 1/16, 1/32 osv. Hver gang tallet bliver mindre og mindre, `tættere på` nul. Men hvor stopper det? Hvor mange gange skal du dividere 1 med 2 for at få nul?? I stedet for at besvare dette spørgsmål foreslår du i analyse en begrænse I dette tilfælde er grænsen.

5. Gennemgå de væsentlige matematiske begreber i algebra, trigonometri og det grundlæggende i matematik. Analyse er afhængig af meget af den matematik, du har lært før. At være velbevandret i alle emner gør det meget lettere at lære og forstå analyser. Nogle emner at genopfriske din viden om er:

6. Få en grafregner. Analyse er ikke let at forstå uden at se, hvad du laver. Grafregnere gør funktioner visuelle, så du bedre kan forstå, hvilke ligninger du har med at gøre. Ofte vises grænserne også på skærmen, og derivaterne og funktionerne beregnes automatisk.
Del 2 af 3: Forstå derivater

1. Analyse bruges til at studere `ændring på et bestemt tidspunkt`. At vide, hvorfor noget ændrer sig på et nøjagtigt tidspunkt, er kernen i analysen. For eksempel giver analyse dig ikke kun hastigheden på en bil, men også hvor meget den hastighed ændrer sig på et givet tidspunkt. Dette er en af de enkleste anvendelser af analyse, men meget vigtig. Forestil dig, hvor vigtig sådan information er for at bestemme den nødvendige hastighed for at få et rumskib til månen!
- Bestemmelse af forandring på et givet tidspunkt har differentiere. Differentiering er den første af de to store analysegrene.

2. Brug derivater til at forstå, hvordan tingene ændrer sig på et givet tidspunkt. Et `afledt` er et fancy ord for noget, der ofte gør eleverne nervøse. Konceptet i sig selv er dog ikke så svært at forstå - det betyder bare "hvor hurtigt noget ændrer sig". De derivater, du vil støde på mest i dagligdagen, har med hastighed at gøre. Men man kalder det normalt ikke `afledt af hastighed`, men blot `acceleration`.

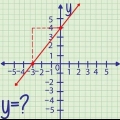
3. Vid, at ændringshastigheden er lig med hældningen mellem to punkter. Dette er en af analysens vigtigste opdagelser. Ændringshastigheden mellem to punkter er lig med hældningen af linjen mellem disse to punkter. Tænk bare på en simpel linje, som ligningen  Hældningen af linjen er 3, hvilket betyder, at for hver ny værdi af
Hældningen af linjen er 3, hvilket betyder, at for hver ny værdi af 
 ændres med 3. Hældningen er den samme som ændringshastigheden: en hældning på tre betyder, at linjen ændres med 3 (bliver tre gange større) for hver ændring i
ændres med 3. Hældningen er den samme som ændringshastigheden: en hældning på tre betyder, at linjen ændres med 3 (bliver tre gange større) for hver ændring i  Hvornår
Hvornår  hvornår
hvornår 
 Hældningen af linjen er 3, hvilket betyder, at for hver ny værdi af
Hældningen af linjen er 3, hvilket betyder, at for hver ny værdi af 
 ændres med 3. Hældningen er den samme som ændringshastigheden: en hældning på tre betyder, at linjen ændres med 3 (bliver tre gange større) for hver ændring i
ændres med 3. Hældningen er den samme som ændringshastigheden: en hældning på tre betyder, at linjen ændres med 3 (bliver tre gange større) for hver ændring i  Hvornår
Hvornår  hvornår
hvornår 

4. Vid, at du kan bestemme hældningen af buede linjer. At bestemme hældningen af en lige linje er relativt enkel: hvor meget ændres  for enhver værdi af
for enhver værdi af  Men komplekse ligninger som
Men komplekse ligninger som  for en kurve, er meget sværere at bestemme. Du kan dog stadig bestemme ændringshastigheden mellem to punkter - bare træk en linje mellem de to punkter og beregn hældningen.
for en kurve, er meget sværere at bestemme. Du kan dog stadig bestemme ændringshastigheden mellem to punkter - bare træk en linje mellem de to punkter og beregn hældningen.
 for enhver værdi af
for enhver værdi af  Men komplekse ligninger som
Men komplekse ligninger som  for en kurve, er meget sværere at bestemme. Du kan dog stadig bestemme ændringshastigheden mellem to punkter - bare træk en linje mellem de to punkter og beregn hældningen.
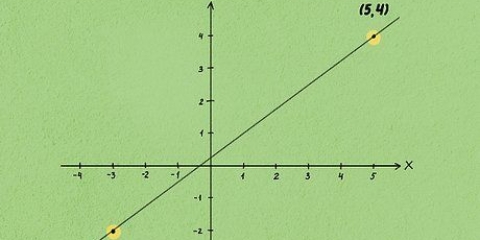
for en kurve, er meget sværere at bestemme. Du kan dog stadig bestemme ændringshastigheden mellem to punkter - bare træk en linje mellem de to punkter og beregn hældningen. du kan vælge to vilkårlige punkter og beregne hældningen. tage
du kan vælge to vilkårlige punkter og beregne hældningen. tage  og
og  Hældningen mellem disse punkter er da lig med
Hældningen mellem disse punkter er da lig med  Det betyder, at skiftet mellem
Det betyder, at skiftet mellem  og
og  er lig med 2.
er lig med 2.
5. Hvis du vil beregne ændringen mere præcist, skal du sørge for, at punkterne er tættere på hinanden. Jo tættere du vælger de to punkter, jo mere præcist er dit svar. Antag, at du vil vide, hvor meget din bil accelererer, når du trykker på gaspedalen. Du vil ikke måle hastighedsændringen mellem dit hjem og supermarkedet, men ændringen i hastigheden fra det øjeblik du træder på speederen. Jo tættere din læsning kommer på den brøkdel af et sekund, jo mere nøjagtig er din beregning af ændringen.

6. Brug uendeligt korte linjer til at bestemme den `øjeblikkelige ændringshastighed`, eller find den afledede. Det er her analyse ofte bliver lidt forvirrende, men det er faktisk resultatet af to simple fakta. Først og fremmest ved du, at hældningen af en linje er lig med, hvor hurtigt den linje ændres. For det andet ved du, at jo tættere punkterne på linjen er på hinanden, jo mere nøjagtig bliver aflæsningen. Men hvordan finder man ændringshastigheden på et givet punkt, hvis hældningen er forholdet mellem to punkter? Svaret: Du vælger to punkter, der er uendeligt tæt på hinanden.

7. Lær, hvordan du bestemmer forskellige derivater. Der er mange forskellige teknikker til at finde en afledt afhængig af ligningen, men de fleste af dem giver mening, når du husker det grundlæggende i afledte ovenfor. Alle derivater er en måde at finde hældningen på en `uendeligt lille` linje. Nu hvor du ved mere om afledt teori, er meget af arbejdet at finde svarene.

8. Bestem de afledte ligninger for at forudsige ændringshastigheden til enhver tid. Det er nyttigt at bestemme ændringshastigheden på ethvert givet tidspunkt ved hjælp af derivater, men det smukke ved analyse er, at du kan oprette en ny model for enhver funktion. Afledt af  for eksempel er
for eksempel er  Det betyder, at du kan finde den afledede for ethvert punkt på en graf
Det betyder, at du kan finde den afledede for ethvert punkt på en graf  ved at substituere i derivatet. På sagen
ved at substituere i derivatet. På sagen  hvorved
hvorved  er den afledte 4, fordi
er den afledte 4, fordi 
 for eksempel er
for eksempel er  Det betyder, at du kan finde den afledede for ethvert punkt på en graf
Det betyder, at du kan finde den afledede for ethvert punkt på en graf  ved at substituere i derivatet. På sagen
ved at substituere i derivatet. På sagen  hvorved
hvorved  er den afledte 4, fordi
er den afledte 4, fordi 
 så skriv det ned som
så skriv det ned som  Dette kaldes Lagranges notation.
Dette kaldes Lagranges notation. Husk at funktionen
Husk at funktionen  afhænger af variablen
afhænger af variablen  Så vi skriver den afledte som
Så vi skriver den afledte som  --- afledt af
--- afledt af  så længe
så længe Dette kaldes Leibniz .s notation.
Dette kaldes Leibniz .s notation.
9. Prøv at huske praktiske eksempler på derivater, hvis du finder det svært at forstå. Det enkleste eksempel er baseret på hastighed, der omfatter en masse forskellige derivater, som vi støder på hver dag. Glem ikke: en afledt er et mål for, hvor hurtigt noget ændrer sig. Tænk på et simpelt eksperiment. Du ruller en kugle på et bord og måler, hvor langt den bevæger sig hver gang og hvor hurtigt. Forestil dig nu, at den rullende marmor følger en linje på en graf - du bruger afledte til at måle de øjeblikkelige ændringer til enhver tid på den linje.
Del 3 af 3: Forstå integraler

1. Vid, at du kan bruge analyse til at finde komplekse områder og volumener. Analyse giver dig mulighed for at måle komplekse former, som ellers er svære at måle. Overvej for eksempel spørgsmålet om at ville vide, hvor meget vand der er i en lang, uregelmæssigt formet sø - det er umuligt at måle hver liter vand individuelt eller at bruge en lineal til at måle søens form. Med analyse kan du studere, hvordan søens kanter ændrer sig, og derefter bruge den information til at finde ud af, hvor meget vand den indeholder.
- Fremstillingen af geometriske modeller og studiet af volumener har integrere. Integralregning er den anden vigtige gren af analysen.

2. Vid, at integration er området under en graf. Integration bruges til at måle rummet under en linje, som giver dig mulighed for at bestemme området med mærkelige eller uregelmæssige former. Tag ligningen  Det ligner et omvendt `U`. Du kan beregne hvor meget plads der er under U`et ved hjælp af integralregning. Du undrer dig måske over, hvad meningen med det er, men tænk på dets brug i fremstillingsprocesserne -- du kan oprette en funktion, der ligner en ny del, og bruge integral aritmetik til at finde arealet af den del, og for at hjælpe dig med at bestille den rigtige mængde materiale.
Det ligner et omvendt `U`. Du kan beregne hvor meget plads der er under U`et ved hjælp af integralregning. Du undrer dig måske over, hvad meningen med det er, men tænk på dets brug i fremstillingsprocesserne -- du kan oprette en funktion, der ligner en ny del, og bruge integral aritmetik til at finde arealet af den del, og for at hjælpe dig med at bestille den rigtige mængde materiale.
 Det ligner et omvendt `U`. Du kan beregne hvor meget plads der er under U`et ved hjælp af integralregning. Du undrer dig måske over, hvad meningen med det er, men tænk på dets brug i fremstillingsprocesserne -- du kan oprette en funktion, der ligner en ny del, og bruge integral aritmetik til at finde arealet af den del, og for at hjælpe dig med at bestille den rigtige mængde materiale.
Det ligner et omvendt `U`. Du kan beregne hvor meget plads der er under U`et ved hjælp af integralregning. Du undrer dig måske over, hvad meningen med det er, men tænk på dets brug i fremstillingsprocesserne -- du kan oprette en funktion, der ligner en ny del, og bruge integral aritmetik til at finde arealet af den del, og for at hjælpe dig med at bestille den rigtige mængde materiale.
3. Vide at vælge et område at integrere. Du kan ikke bare integrere en hel funktion. For eksempel,  er en diagonal linje, der fortsætter for evigt, og du kan ikke integrere det hele, for det ville aldrig stoppe. Når du integrerer funktioner, skal du vælge et område, såsom alle punkter imellem
er en diagonal linje, der fortsætter for evigt, og du kan ikke integrere det hele, for det ville aldrig stoppe. Når du integrerer funktioner, skal du vælge et område, såsom alle punkter imellem og
og 
 er en diagonal linje, der fortsætter for evigt, og du kan ikke integrere det hele, for det ville aldrig stoppe. Når du integrerer funktioner, skal du vælge et område, såsom alle punkter imellem
er en diagonal linje, der fortsætter for evigt, og du kan ikke integrere det hele, for det ville aldrig stoppe. Når du integrerer funktioner, skal du vælge et område, såsom alle punkter imellem og
og 

4. Hvordan beregner man arealet af et rektangel?. Antag at du har en flad linje over en graf, som f.eks  For at finde området under det, find arealet af et rektangel imellem
For at finde området under det, find arealet af et rektangel imellem  og
og  Dette er nemt at måle, men det fungerer ikke med bølgede linjer, fordi du ikke nemt kan konvertere dem til rektangler.
Dette er nemt at måle, men det fungerer ikke med bølgede linjer, fordi du ikke nemt kan konvertere dem til rektangler.
 For at finde området under det, find arealet af et rektangel imellem
For at finde området under det, find arealet af et rektangel imellem  og
og  Dette er nemt at måle, men det fungerer ikke med bølgede linjer, fordi du ikke nemt kan konvertere dem til rektangler.
Dette er nemt at måle, men det fungerer ikke med bølgede linjer, fordi du ikke nemt kan konvertere dem til rektangler.
5. Vid, at i integralregning lægges mange små rektangler sammen for at finde arealet af et område. Hvis du forstørrer en kurve enormt, ligner den en lige linje. Du ser dette hver dag -- du kan ikke se jordens krumning, fordi du er så tæt på jordens overflade. Integration skaber et uendeligt antal små rektangler under en kurve, der er så små, at de grundlæggende er flade, så du kan tælle dem. Alle disse rektangler lagt sammen danner arealet af området under en kurve.

6. Vide, hvordan man læser og skriver integraler korrekt. Integraler består af 4 dele. Et typisk integral ser sådan ud:


 er symbolet for integration (dette er faktisk et strakt S).
er symbolet for integration (dette er faktisk et strakt S). er funktionen. Hvis det er inde i integralet, kaldes det de integral.
er funktionen. Hvis det er inde i integralet, kaldes det de integral. til sidst, som fortæller dig, hvilken variabel du integrerer og til hvad. Fordi funktionen
til sidst, som fortæller dig, hvilken variabel du integrerer og til hvad. Fordi funktionen  kommer an på
kommer an på  er det, du integrerer dig imod.
er det, du integrerer dig imod. vil være, så vær forsigtig med, hvad du skriver ned.
vil være, så vær forsigtig med, hvad du skriver ned.
7. Lær mere om at finde integraler. Integralregning kommer i mange former, og du skal lære en masse forskellige formler for at integrere hver funktion. Men de følger alle ovenstående principper: integration er summen af et uendeligt antal ting.

8. Vid, at integration er det omvendte af differentiering og omvendt. Dette er en tommelfingerregel, der er så vigtig, at den har fået sit eget navn: Grundsætningen for Integralkonto. Da integration og differentiering er så tæt forbundet, kan en kombination af de to bruges til at måle ændringshastigheden, accelerationen, hastigheden, placeringen, bevægelsen osv. at bestemme, uanset hvilke oplysninger du har.

9. Ved, at integration også giver dig mulighed for at kontrollere volumen af 3D-objekter. Spinning af en flad form er en måde at skabe 3D solids på. Forestil dig bare en mønt på bordet, der snurrer - læg mærke til, hvordan mønten ser ud til at tage form som en kugle, når den drejer. Dette koncept giver dig mulighed for at bestemme volumen ved en proces kendt som `volumen ved rotation`.
Tips
- Øvelse gør mester, så gør øveøvelserne i din lærebog – også dem, din lærer ikke har angivet – og tjek dine svar, så du bedre forstår begreberne.
- Hvis du ikke kan finde ud af noget, så spørg din lærer.
Artikler om emnet "Forståelse af analyser"
Оцените, пожалуйста статью
Populær