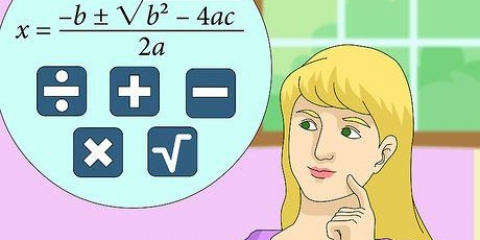Eksempel 1: Sinus på 30 grader er 0,50. Det betyder, at den modsatte side af en 30 graders vinkel er nøjagtigt halvdelen af hypotenusens længde. Eksempel 2: Denne relation kan bruges til at finde længden af hypotenusen i en trekant med en vinkel på 30 grader med en modsat side på 18 cm. Hypotenusen ville da være lig med 36 cm. 
Sinus (Sinus) Cosinus (Cos) Tangent (Tan) Skærelinje (sek.) Cosecant (Csc) Cotangens (Cotang) Månen har en forudsigelig cyklus på omkring 29,5 dage. Tænk på at måle tidevandet på en bestemt strand. Under højvande når den en vis højde og synker derefter til ebbe. Fra lavvande stiger vandet højere på stranden, indtil tidevandet er igen. Denne cyklus ville fortsætte i det uendelige og kan tegnes som en trigonometrisk funktion, såsom en cosinus. Skriv også eventuelle spørgsmål ned, du vil stille din lærer. I de fleste bøger står svarene til en række øvelser bagerst. På denne måde kan du tjekke dit arbejde. Hvis din lærer foretrækker at undervise uden afbrydelser, så stil dine spørgsmål før eller efter undervisningen. Husk, det er lærerens opgave at hjælpe dig med at lære trigonometri, så vær ikke genert.
Lær trigonometri
Indhold
Trigonometri er den gren af matematikken, der beskæftiger sig med trekanter og cyklusser. Trigonometriske funktioner bruges til at beskrive vinklernes egenskaber, relationerne i en trekant og graferne for en tilbagevendende cyklus. At lære trigonometri hjælper med at forstå, visualisere og plotte disse relationer og cyklusser. Hvis du kombinerer selvstudie med opmærksomhed under lektionerne, kan du begynde at forstå de grundlæggende trigonometriske begreber og sandsynligvis begynde at lægge mærke til cyklusser i verden omkring dig.
Trin
Metode 1 af 4: Fokus på trigonometriske nøglebegreber

1. Definer delene af en trekant. I sin kerne er trigonometri studiet af forhold i trekanter. En trekant har tre sider og tre vinkler. Per definition er summen af vinklerne i en trekant 180 grader. Du skal sætte dig ind i trekanter og trekantsterminologi for at kunne mestre trigonometri godt. Nogle almindeligt anvendte udtryk:
- Hypotenus - den længste side af en trekant.
- Stump vinkel en vinkel større end 90 grader.
- Akut vinkel - En vinkel på mindre end 90 grader.

2. Lær, hvordan du får enheden til at cirkle. Med en enhedscirkel kan man skalere en trekant, så hypotenusen er lig med én. Dette er nyttigt, fordi det kan udtrykke trigonometriske funktioner, såsom sinus og cosinus, i procenter. Når du forstår enhedscirklen, kan du bruge de trigonometriske værdier af en given vinkel til at besvare spørgsmål om trekanter med disse vinkler.

3. Kend de trigonometriske funktioner. Der er seks funktioner, der er afgørende for at forstå trigonometri. Sammen definerer de relationerne i en trekant og giver dig mulighed for at forstå en trekants unikke egenskaber. Disse seks funktioner er:
4. Forståelse af relationer. En af de vigtigste ting at forstå om trigonometrifunktioner er, at alle funktioner er indbyrdes forbundne. Mens værdierne for sinus, cosinus, tangent osv. alle har deres egen applikation, de er mest nyttige på grund af de relationer, der eksisterer mellem dem. Enhedscirklen begrænser disse relationer, så de er nemme at forstå. Når du forstår enhedscirklen, kan du bruge de relationer, den beskriver, til at modellere andre problemer.
Metode 2 af 4: Forståelse af anvendelserne af trigonometri
1. Forstå den grundlæggende videnskabelige brug af trigonometri. Udover at studere trigonometriske funktioner, bare fordi de kan lide trigonometri, anvendes disse egenskaber også praktisk af matematikere og videnskabsmænd. Trigonometri kan bruges til at finde værdier for vinkler eller linjestykker. Du kan også beskrive cykliske egenskaber ved at tegne dem som trigonometriske funktioner.
- For eksempel kan bevægelsen af en spiralfjeder beskrives som en sinusbølge ved hjælp af en graf.
2. Tænk på kredsløbene i naturen. Nogle gange kæmper folk for at forstå abstrakte begreber i matematik eller naturvidenskab. Når du indser, at disse begreber er til stede i verden omkring dig, kan du ofte se på dem i et nyt lys. Se efter ting i dit liv, der sker i cyklusser, og prøv at relatere dem til trigonometri.
3. Visualiser, hvordan man studerer naturlige cyklusser. Når du først indser, at naturen er fuld af cyklusser, kan du begynde at tænke på, hvordan du kan studere disse cyklusser. Tænk på, hvordan en graf over disse cyklusser ville se ud. Fra grafen kan du så udlede en ligning til at beskrive det fænomen, du har observeret. Dette giver trigonometriske funktioner mening, så du bedre kan forstå deres anvendelighed.
Metode 3 af 4: Undersøg fremad
1. Læs kapitlet. Trigonometriske begreber er svære for mange mennesker at forstå med det samme. Læser du kapitlet før behandlingen i klassen, bliver du mere fortrolig med stoffet. Jo oftere du ser materialet, jo bedre vil du være i stand til at relatere de forskellige begreber i trigonometri til hinanden.
- Hermed kan du gennemgå alle begreber, du har problemer med inden undervisningen.
2. Hold en notesbog. At gennemse en bog er bedre end ingenting, men det er ikke den grundige form for læsning, der vil lære dig trigonometri. Hold detaljerede noter om hvert kapitel, du læser. Husk, at trigonometri er kumulativ, og begreberne bygger på hinanden, så dine noter fra tidligere kapitler kan hjælpe dig med at forstå det næste kapitel.
3. Lav øvelser fra bogen. Nogle mennesker er gode til at visualisere trigonometri, men du bliver også nødt til at lave øvelser. For at sikre dig, at du virkelig forstår materialet, lav nogle øvelser før undervisningen. På denne måde ved du præcis, hvad du har brug for hjælp til i timen, hvis du har problemer med noget.
4. Medbring dit studiemateriale til klassen. At medbringe dine noter og øve øvelser til klassen vil give dig noget at henvise til. Dette genopfrisker de ting, du allerede forstår, og peger dig på begreber, der skal forklares bedre. Få svar på alle de spørgsmål, du skrev ned, mens du læste.
Metode 4 af 4: At tage noter i undervisningen
1. Tag noter i den samme notesbog. Trigonometriske begreber er alle relaterede. Det er bedst at opbevare alle dine noter ét sted, så du kan henvise til dem senere. Udpeg en specifik notesbog eller mappe til dit studium af trigonometri.
- Du kan også lave dine øvelsesopgaver her.
2. Gør trigonometri til din prioritet i klassen. Brug ikke din time til at chatte eller indhente lektier fra en anden klasse. I trigonometritimen er det vigtigt at have fuld fokus på lektionen og opgaverne. Skriv de noter ned, som læreren har skrevet på tavlen eller markeret som vigtige.
3. Bliv involveret i klasseværelset. Meld dig frivilligt til at løse problemer på tavlen eller del dine svar på øvelsesproblemer. Stil spørgsmål, hvis du ikke forstod noget. Hold kommunikationen så åben og fleksibel som muligt, så vidt din lærer tillader det. Dette vil gøre det meget nemmere at lære og have det sjovt i trigonometri.
4. Lav derefter flere øvelsesopgaver. Lav alle de lektier, du har fået. Hjemmeopgaver er gode indikatorer for testspørgsmål. Sørg for, at du forstår hver opgave. Hvis du ikke har fået lektier, så arbejd med de problemer fra bogen, der matcher begreberne i den sidste lektion.
Tips
- Husk at matematik er en måde at tænke på og ikke kun formler at huske.
- Lær mere om algebra og geometri.
Advarsler
- Du kan ikke lære trigonometri ved at slå. Du bliver nødt til at forstå de underliggende begreber.
- Stempling til en test i trigonometri vil praktisk talt aldrig fungere.
Artikler om emnet "Lær trigonometri"
Оцените, пожалуйста статью
Populær