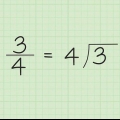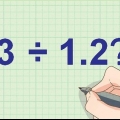I øvelse #1 (5 til 65), 5 er nævneren og 6 er det første ciffer i tælleren (65). 5 går i 6 én gang, så sæt et 1 på divisionstegnet over 6’eren. I øvelse #2 (3.136), 3 (divisoren) passer ikke helt ind i 1 (det første ciffer i tælleren). I dette tilfælde skal du skrive et 0 over divisionstegnet, over 1. 
I øvelse #1 (5 til 65), gange tallet over stregen (1) med nævneren (5), hvilket resulterer i 1 x 5 = 5, og placer svaret (5) lige under 6 af 65. I øvelse #2 (`3.136) der er et nul over divisionstegnet, så hvis du gange dette med 3 (nævneren), er resultatet nul. Skriv et nul på en ny linje lige under 1 af 136. 
I øvelse #1 (5 til 65), trække 5 (produktet i den nye række) fra 6 over det (det første ciffer i tælleren): 6 - 5 = 1. Placer resultatet (1) i en anden ny række lige under 5. I øvelse #2 (3.136) trække 0-tallet (produktet i den nye række) fra 1-tallet øverst til højre (det første ciffer i tælleren). Placer resultatet (1) i en anden ny række direkte under 0-tallet. 
I øvelse #1 (5 til 65), nedbring 5 ud af 65, så det er ved siden af 1 opnået ved at trække 5 fra 6. Der er nu 15 i denne række. I øvelse #2 (3.136), sænk de 3 af 136 og placer dem ved siden af 1, hvilket giver dig 13. 
Til at fortsætte med 5 til 65, divider det nye tal (15) med 5 (nævneren), og skriv resultatet (3, fordi 15 ÷ 5 = 3) til højre for 1`eren over delingsskiltet. Så gange du disse 3 over divisionstegnet med 5 (nævneren) og skriver resultatet (15, fordi 3 x 5 = 15) under 15 under delingstegnet. Træk til sidst 15 fra 15 og skriv 0 i en ny nederste række. Eksempelopgave #1 er nu færdig, da der ikke er flere tal at få ned i nævneren. Svaret (13) er over divisionstegnet. 
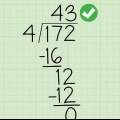
Til 3.136: Bestem hvor mange gange 3 går helt over i 13, og skriv svaret (4) til højre for 0-tallet over divisionstegnet. Gang derefter 4 med 3 og skriv svaret (12) under 13. Træk til sidst 12 fra 13 og skriv svaret (1) under 12. 
Til 3.136: Fortsæt processen til næste runde. Sænk de 6 af 136, og efterlad 16 i den nederste række. Del 16 med 3 og skriv resultatet (5) over divisionstegnet. Gang 5 med 3 og skriv resultatet (15) i en ny nederste række. Træk 15 fra 16 og skriv resultatet (1) i en ny nederste række. Da der ikke er flere cifre at inkludere i tælleren, er du færdig med problemet, og 1`eren på den nederste linje er resten (det tal, der er tilbage). Skriv det over divisionstegnet, eventuelt med et `r.`før, så dit endelige svar `45 r.1` bliver. 

I denne opgave passer 4 (nævneren) ind i 5 (det første ciffer i tælleren) én gang, med en rest på 1 (5 ÷ 4 = 1 r.1). Placer kvotienten, 1, over den lange delelinje. Placer en lille hævet 1 ved siden af 5 for at minde dig selv om, at du havde en rest på 1. De 518 under delelinjen skulle nu se sådan ud: 518. 
I opgaven er tallet dannet af resten og det andet tal i tælleren 11. nævneren (4), går ind i 11 to gange, hvilket efterlader en rest på 3 (11 ÷ 4 = 2 r.3) forbliver. Skriv 2 over divisionslinjen (hvis du får 12) og 3 som et hævet tal ved siden af 1 i 518. Den originale tæller, 518, skulle nu se sådan ud: 518. 
I opgaven er 38 det næste (og sidste) tal i tælleren -- resten 3 fra det forrige trin, og tallet 8 er det sidste led i tælleren. Nævneren (4) går i 38 ni gange med en rest på 2 (38 ÷ 4 = 9 r.2), fordi 4 x 9 = 36, hvilket er to mindre end 38. Skriv denne sidste rest (2) over divisionslinjen for at fuldføre dit svar. Så dit sidste svar over skillelinjen er 129 r.2.. 

I dette eksempelopgave vender vi 5/8 om, så 8`eren er øverst og 5`eren er nederst. 
For eksempel: 3/4 x 8/5. 
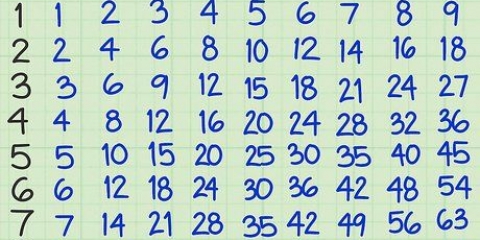
I dette tilfælde er tællerne 3 og 8, og 3 x 8 = 24. 
Nævnerne er 4 og 5 i opgaven, og 4 x 5 = 20. 
I opgaven: 3/4 x 8/5 = 24/20. 
I tilfælde af 24/20 er 4 det største tal, der går jævnt i både 24 og 20. Du kan bekræfte dette ved at skrive alle divisorerne for begge tal og vælge det største tal, der er en divisor af begge: 24: 1, 2, 3, 4, 6, 8, 12, 24 20: 1, 2, 4, 5, 10, 20 Da 4 er den største fælles divisor af 24 og 20, skal du dividere begge tal med 4 for at forenkle brøken. 24/4 = 6 20/4 = 5 24/20 = 6/5. Så: 3/4 5/8 = 6/5 
I opgaven går 5 i 6 én gang med en rest på 1. Så det nye heltal er 1, den nye tæller er 1, og nævneren forbliver 5. Resultatet: 6/5 = 1 1/5. 

I opgaven: 8 - 5 = 3. 
Dermed: 3 3 = 3. 

I opgaven er alt hvad du skal gøre at flytte decimaltegnet én position for både nævneren og tælleren. Altså: 0,5 bliver til 5 og 65,5 bliver til 655. Men hvis tallene i opgaven var 0,5 og 65,55, ville du flytte decimaltegnet to pladser i 65,55, hvilket gør det til 6555. Som et resultat bør du også flytte decimaltegnet 0,5 to steder. For at gøre dette skal du tilføje et nul til slutningen og gøre det til 50. 
I erklæringen kommer decimalen i 655 efter de sidste 5 (som 655,0). Så skriv decimaltegnet over divisionslinjen direkte over decimaltegnet i 655. 
Divider hundrededelen (6) med 5. Du får så 1, og resten 1. Placer 1 på hundredepladsen oven på den lange divisionslinje, og træk 5 fra 6 under tallet seks. Resten, 1, er tilbage. Få de første fem ned i 655, og du får tallet 15. Divider 15 med 5 og du får 3. Placer de tre over det lange divisionstegn ved siden af 1. Få de sidste 5 ned. Divider 5 med 5 og du får 1 -- placer 1`eren over det lange divisionstegn. Der er ingen rest, da 5 går en gang ud af 5. Svaret er tallet over det lange divisionstegnet (131), altså 655 5 = 131. Hvis du trækker en lommeregner frem, vil du se, at dette også er svaret på den oprindelige inddeling: 65,5 0,5.
Lav divisionssummer
Indhold
Division er en af de fire store aritmetiske operationer, sammen med addition, subtraktion og multiplikation. Udover hele tal kan du også dividere decimaler, brøker eller eksponenter. Du kan lave lang division eller, hvis et af tallene er et enkelt ciffer, en kort division. Begynd dog at mestre lang division, for det er nøglen til hele operationen.
Trin
Metode 1 af 5: Lang division

1. Skriv problemet ud ved hjælp af enlangt delingsskilt. Det lange divisionstegn ( 厂 ) ligner en `slutparentes` med et tal under. Placer nævneren, det tal, du dividerer, uden for tegnet for lange division, og tælleren, det tal, du deler, inden for tegnet for lange division .
- Eksempel på problem #1 (begynder): 65 5. Placer de 5 uden for divisionen, og de 65 indeni den. Det skal se ud 5 til 65, men med de 65 under den vandrette linje.
- Eksempel øvelse #2 (avanceret): 136 3. Placer de 3 uden for divisionen, og de 136 indeni den. Det skal se ud 3.136, men med de 136 under den vandrette linje.

2. Divider det første ciffer i tælleren med nævneren. Med andre ord, find ud af, hvor mange gange nævneren (tallet uden for divisionstegnet) går ind i det første ciffer i tælleren. Placer heltalsresultatet over divisionstegnet lige over det første ciffer i nævneren.

3. Gang tallet over divisionstegnet med nævneren. Tag det tal, du skrev lige over divisionen, og gang det med nævneren (tallet til venstre for divisionen). Skriv resultatet i en ny række under tælleren, justeret med det første ciffer i tælleren.

4. Træk produktet (resultatet af multiplikationen) fra det første ciffer i tælleren. Med andre ord, træk det tal, du lige har skrevet i den nye linje under tælleren, fra tallet i tælleren direkte over det. Skriv resultatet i en ny række, justeret under subtraktionens tal.

5. Bring det andet ciffer i tælleren ned. Bring det andet ciffer i tælleren ned til den nye nederste række, lige til højre for resultatet af den subtraktion, du lige har fået.

6. Gentag lang division (opgave #1). Denne gang skal du bruge tælleren (tallet til venstre for divisionstegnet) og det nye tal på nederste række (resultatet af din første matematikrunde og det ciffer, du bar ned). Som før skal du dividere, gange og trække dine tal fra for at få resultatet.

7. Gentag lang division (opgave #2). Start som før med division, multiplikation og derefter subtraktion.

8. Lav endnu en lang divisionsrunde og du får resten (opgave #2). Når du er færdig med dette problem, skal du bemærke, at der er en rest (det vil sige et tal tilbage i slutningen af din beregning). Du sætter denne pause ved siden af hele dit svar.
Metode 2 af 5: Kort division

1. Brug en bindestreg til at skrive problemet. Placer nævneren, det tal, du dividerer med, uden for (og til venstre for) divisionslinjen. Placer tælleren, det tal du skal dividere, inden for (til højre for og under) divisionslinjen.
- Til hurtig at dele, må nævneren kun bestå af et ciffer.
- Opgave: 518 4. I dette tilfælde vil de 4 være uden for divisionslinjen, og 518 vil være inden for den.

2. Divider det første ciffer i tælleren med nævneren. Med andre ord, bestem, hvor mange gange tallet uden for skillelinjen passer ind i det første ciffer i tallet inde i skillelinjen. Skriv resultatets heltal over divisionsbjælken, og skriv eventuel rest i hævet ved siden af det første ciffer i tælleren.

3. Divider resten og det andet ciffer af tælleren med nævneren. Behandl det hævede tal, der angiver resten, som et fuldgyldigt ciffer, og kombiner det med tællerens ciffer umiddelbart til højre for det. Bestem, hvor mange gange nævneren går helt ind i dette nye 2-cifrede tal, og skriv hele tallet og resten, som du gjorde før.

4. Gentag dette, indtil du har gennemgået hele tælleren. Fortsæt med at bestemme, hvor mange gange nævneren går ind i tallet dannet af det næste ciffer i tælleren og resten i hævet umiddelbart til venstre for det. Når du har gennemgået alle cifrene på tælleren, har du fået dit svar.
Metode 3 af 5: Opdeling af brøker

1. Skriv divisionssummen, så de to brøker ligger ved siden af hinanden. Til dele brøker, skriv den første brøk efterfulgt af divisionssymbolet (÷) og derefter den anden brøk.
- Udsagnet kunne for eksempel være noget som: 3/4 5/8. For nemheds skyld skal du bruge vandrette snarere end diagonale linjer til at adskille tælleren (øverste tal) og nævneren (nederste tal) for enhver brøk.

2. Vend tælleren og nævneren for den anden brøk om. Den anden fraktion bliver sin egen inverse.

3. Skift divisionsbjælken til et multiplikationstegn. For at dividere brøker skal du gange den første brøk med den gensidige af den anden.

4. Multiplicer brøkernes tællere. Følg samme procedure, som når du multiplicerer to brøker.

5. Multiplicer brøkernes nævnere på samme måde. Igen, det er præcis, hvad du ville gøre for at gange to brøker.

6. Placer produktet af tællere over produktet af nævnerne. Nu hvor du har ganget tællere og nævnere af begge brøker, kan du danne produktet af de to brøker.

7. Forenkle brøken, hvis det er nødvendigt. For at forenkle brøken, bestemme den største fælles divisor, eller det største tal, der passer ind i begge tal i sin helhed, og divider derefter både tælleren og nævneren med det tal.

8. Omskriv brøken som et blandet tal, hvis det er nødvendigt. For at gøre dette skal du dividere tælleren med nævneren og skrive svaret som et heltal. Resten (det tal, der er tilbage) er tælleren for den nye brøk. Brøkens nævner forbliver den samme.
Metode 4 af 5: Opdeling af eksponenter

1. Sørg for, at eksponenterne har samme base. Du kan dividere eksponenter hvis de har samme base. Hvis de ikke har den samme base, bliver du nødt til at manipulere dem, indtil de har, hvis du kan.
- Hvis du lige er begyndt med dette, skal du først lave et problem, hvor begge eksponenter allerede har den samme base. For eksempel: 3 3.

2. Træk eksponenterne fra hinanden. Træk blot den anden eksponent fra den første. Du skal ikke bekymre dig om basen lige nu.

3. Placer den nye eksponent over den oprindelige base. Bare skriv den nye eksponent over den oprindelige base. Det er alt!
Metode 5 af 5: Division af decimaltal

1. Skriv opgaven med en bindestreg. Placer nævneren, det tal, du dividerer med, uden for (og til venstre for) den lange divisionsbjælke, og tælleren, det tal, du dividerer, inden for den lange divisionsbjælke. Til dividere decimaler, konverter decimaler til heltal først.
- I eksemplet 65,5 0,5 er placeret 0,5 uden for delelinjen og 65,5 inden for den.

2. Flyt decimalpunkterne ligeligt for at skabe to heltal. Skub blot decimaltegnene til højre, indtil de er i slutningen af hvert tal. Sørg for at flytte dem det samme antal positioner for hvert tal -- hvis du skal flytte decimaltegnet to steder i nævneren, gør det samme for tælleren.

3. Placer decimaltegnet direkte over divisionslinjen. Sæt en decimal på det lange divisionstegnet direkte over decimalen i tælleren.

4. Løs problemet ved at udføre lang division. Gør følgende for at dividere 655 med 5:
Artikler om emnet "Lav divisionssummer"
Оцените, пожалуйста статью
Populær