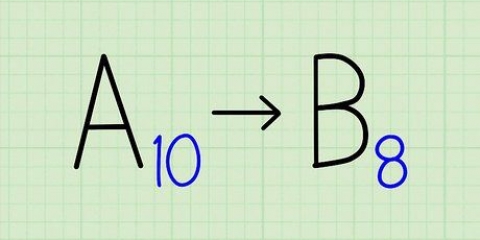11 > 1, altså 11 "passer ikke" 1. Skriv et 0 som det første ciffer i kvotienten (over det første ciffer i dividenden). 
Sænk det næste ciffer i udbyttet. 11 > 10. Skriv et 0 i kvotienten. Bring det næste tal ned. 11 < 101. Skriv et 1 i kvotienten. 
Skriv divisoren under udbyttet. Her skriver vi dette som 11 under de første tre cifre (101) af udbyttet. Beregn 101 - 11 for resten, 10. Gennemgå, hvordan du trækker binære tal fra, hvis du ikke kan huske det. 
Skriv 11 under 100 og træk disse tal fra for at få 1. Sænk det sidste ciffer i udbyttet, og du får 11 som svar. 11 = 11, så du skriver 1 som det sidste ciffer i kvotienten (svaret). Der er ingen rest, så opgaven er fuldført. Svaret er 00111, eller enklere, 111. 
At dividere binære tal resulterer ofte i gentagelse af tal efter decimalkommaet, oftere end dem, der forekommer med decimalnotation. Dette refereres til med det mere generelle udtryk "radix punkt" som du støder på i hvert talsystem, fordi du har "decimaltegnet" kun stødt på inden for decimalsystemet. 

Find komplementet til enerne i det andet led ved at trække hvert ciffer fra 1. Du kan nemt gøre dette med binære tal ved at sætte hver 1 til 0 og hver 0 til 1. I vores eksempel er 011 lig med 100. Tilføj 1 til resultatet: 100 + 1 = 101. Dette kaldes 2`erens komplement. Vi skal nu betragte en minussum som en tillægssum. Essensen er, at vi betragter problemet, som om vi tilføjede et negativt tal i stedet for at trække et positivt tal fra, efter at have gennemført proceduren. Tilføj resultatet til den første term. Løs summen: 111 + 101 = 1100. Udelad det første ciffer (bær ciffer). Fjern det første ciffer fra dit svar for at få det endelige resultat. 1100 → 100. 

2`s komplement af 000101 = 111010 + 1 = 111011 100011 + 111011 = 1011110 Udelad det første ciffer (bæringen) → 011110 

011110 + 111011 = 1011001 → 011001 (kvotient 1+1=10) 011001 + 111011 = 1010100 → 010100 (kvotient 10+1=11) 010100 + 111011 = 1001111 → 001111 (11+1=100) 001111 + 111011 = 1001010 → 001010 (100+1=101) 001010 + 111011 = 10000101 → 0000101 (101+1=110) 0000101 + 111011 = 1000000 → 000000 (110+1=111) 0 er mindre end 101, så nu kan vi stoppe. Kvotienten 111 er svaret på underproblemet. Resten er det endelige resultat af vores minsum, i dette tilfælde 0 (ingen hvile).
Opdeling af binære tal
At dividere binære tal kan løses ved hjælp af lang division, en bekvem metode til at lære dig selv proceduren eller skrive et simpelt computerprogram. Alternativt tilbyder komplementmetoden med gentagen subtraktion en tilgang, som du måske ikke er bekendt med, selvom den ikke er meget udbredt i programmering. Maskinsprog bruger normalt en estimeringsalgoritme for større effektivitet, men disse er ikke beskrevet her.
Trin
Metode 1 af 2: Brug af lang division

1. Gå over decimal lang division igen. Hvis det er et stykke tid siden, du lavede lang division med almindelige decimaltal (grundlag 10), skal du gennemgå grunden for opgaven 172 ÷ 4. Ellers spring dette over og gå til næste trin for at lære denne procedure for binære tal.
- Det udbytte er divideret med divisor, og svaret er det kvotient.
- Sammenlign divisor med det første ciffer i udbyttet. Hvis divisor er det største tal, skal du fortsætte med at tilføje cifre til dividenden, indtil divisor er det mindste tal. (Som et eksempel, når vi beregner 172 ÷ 4, sammenligner vi 4 og 1, finder vi, at 4 > 1, og sammenlign derefter 4 med 17.)
- Skriv det første ciffer i kvotienten over det sidste ciffer i det udbytte, der bruges til sammenligning. Efter at have sammenlignet 4 og 17, bemærker vi, at 4 går ind i 17 fire gange, så vi skriver 4 som det første ciffer i vores kvotient, over 7.
- Multiplicer og træk fra for at finde resten. Gang kvotienten med divisor, i dette tilfælde 4 x 4 = 16. Skriv de 16 under de 17, og gør derefter 17 - 16 for resten, 1.
- Gentage. Igen sammenligner vi divisor 4 med det næste ciffer, 1, vi bemærker, at 4 > 1, og "tage med" vi flytter det næste ciffer i udbyttet ned for i stedet at sammenligne 4 med 12. 4 går ind i 12 tre gange uden rest, så vi kan skrive 3 som det næste ciffer i kvotienten. Svaret er 43.

2. Opret en binær lang divisionsopsætning. Antag, at vi som eksempel bruger 10101 ÷ 11. Skriv dette som lang division, med 10101 som udbytte og 11 som divisor. Lad plads over den for at skrive kvotienten, og skriv dine beregninger under den.

3. Sammenlign divisor med det første ciffer i udbyttet. Dette fungerer på samme måde som decimal lang division, men er faktisk meget nemmere i binær form. Enten kan du ikke dividere tallet med divisoren (0), eller også passer divisoren ind én gang (1):

4. Tag nu det næste tal og gentag, indtil du får 1. Her er de næste par trin fra vores eksempel:

5. Bestem resten. som i decimal lang division gange vi det ciffer, vi lige har fundet (1) med divisoren (11), og skriver resultatet under vores dividende på en linje med det ciffer, vi lige har beregnet. I binær form kan vi gøre dette hurtigere, fordi 1 x divisor altid er lig med divisor:

6. Fortsæt indtil problemet er løst. Bring det næste ciffer fra forhandleren til resten nedenfor for at få 100. Fordi 11 < 100 skriver du et 1 som det næste ciffer i kvotienten. Fortsæt med at løse problemet som før:

7. Tilføj et radix-punkt, hvis det er nødvendigt. Nogle gange er resultatet ikke et heltal. Hvis du stadig har en rest efter at have brugt det sidste ciffer, skal du tilføje en ".0" til udbyttet og en "." til din kvotient, så du kan bringe et tal mere ned og komme videre. Bliv ved med at gøre dette, indtil du når den ønskede nøjagtighed, og rund derefter dit svar af. På papir kan du afrunde ved at udelade 0 eller, hvis det sidste ciffer er et 1, trække det fra og lægge 1 til det sidste ciffer. Ved programmering skal du bruge en af standardafrundingsalgoritmerne for at undgå fejl ved konvertering mellem binære og decimale tal.
Metode 2 af 2: Brug af komplementmetoden

1. Forstå den grundlæggende idé. En måde at løse divisioner - for enhver base - er at blive ved med at trække divisoren fra dividenden og derefter resten, ved at regne ud, hvor mange gange du kan blive ved med at gøre dette, før du når et negativt tal. Her er et eksempel på grundtallet 10, opgaven 26 ÷ 7:
- 26 - 7 = 19 (1 gange fratrukket)
- 19 - 7 = 12 (2 gange fratrukket)
- 12 - 7 = 5 (3 gange fratrukket)
- 5 - 7 = -2. Negativt tal, så op igen. Svaret er 3 med en rest på 5. Bemærk, at denne metode ikke tager højde for decimaltal.

2. Lær at trække fra ved hjælp af komplementer. Selvom du nemt kan anvende ovenstående metode til binære tal, kan vi også bruge en mere effektiv metode, som kan spare dig tid ved programmering af binære divisioner. Dette kaldes den binære komplementmetode. Her er det grundlæggende, hvor vi beregner 111 - 011 (sørg for, at begge tal har samme længde):

3. Kombiner de to ovenstående begreber. Nu ved du, hvordan subtraktionsmetoden til at løse divisioner fungerer, og 2`erens komplementmetode til at løse summen af minusser. Du kan kombinere de to til én metode til at løse divisionsproblemer ved at bruge nedenstående trin. Hvis du vil, kan du prøve selv at finde ud af det, før du fortsætter.

4. Træk divisor fra udbyttet ved at tilføje 2`erens komplement. Lad os finde ud af følgende problem: 100011 ÷ 000101. Det første trin er at løse 100011 - 000101 ved hjælp af 2`s komplementmetode, så det bliver en sum:

5. Tilføj 1 til kvotienten. I et computerprogram er det det punkt, hvor du øger kvotienten med 1. Lav en note på papiret i et hjørne et sted, hvor det ikke vil ødelægge resten af dit arbejde. Vi har nu med succes lavet et minsum én gang, så kvotienten er indtil videre 1.

6. Gentag ved at trække divisor fra resten. Resultatet af vores sidste beregning er resten tilbage efter divisor én gang "gik ind". Fortsæt med at tilføje divisorens 2`er-komplement og subtrahere carry. Tilføj 1 til kvotienten hver gang, og fortsæt, indtil du får en rest svarende til din mindre divisor:
Tips
- Inkrement-, reduktions- eller stakinstruktionerne bør overvejes, før du anvender en binær beregning på et sæt af maskinudsagn.
- 2`erens komplementmetode til subtraktion virker ikke, hvis tallene består af et andet antal cifre. Tilføj ekstra nuller til det mindre tal for at løse dette.
- Ignorer det signerede ciffer i binære tal med fortegn, før du laver beregningen, undtagen når du forsøger at finde ud af, om et svar er positivt eller negativt.
Artikler om emnet "Opdeling af binære tal"
Оцените, пожалуйста статью
Populær