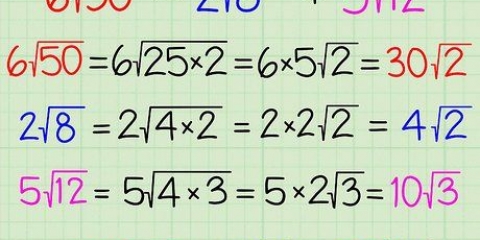Eks. 1: √(18) x √(2) = √(36) Eks. 2: √(10) x √(5) = √(50) Eks. 3: √(3) x √(9) = √(27) 
Eks. 1: √(36) = 6. 36 er et kvadrat, fordi det er et produkt af 6 x 6. Kvadratroden af 36 er kun 6. Eks. 2: √(50) = √(25 x 2) = √([5 x 5] x 2) = 5√(2). Mens 50 ikke er et kvadrattal, er 25 en faktor på 50 (fordi det passer præcist to gange) og er et perfekt kvadrat. Du kan faktor 25 (5 x 5) og placere et 5 uden for radikalet for at forenkle ligningen. Du kan tænke på det sådan her: Hvis du sætter 5`eren tilbage under det radikale tegn, vil det formere sig af sig selv og blive 25 igen. Eks. 3:√(27) = 3. 27a er en perfekt terning (tredje potens), fordi det er produktet af 3 x 3 x 3. Kvadratroden af 27 er derfor 3. 

Eks. 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20) Eks. 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18) 
3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5) 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2) 

√(5) x √(2) = ? 

--> √(5) = √(5) --> √(2) = √(2) 
√(5) = √(5 x 5) = √25 √(2) = √(2 x 2 x 2) = √8 

Gang gulerodsnumre sammen
Indhold
Rodsymbolet (√) repræsenterer kvadratroden af et tal. Du kan støde på rodsymbolet i matematik, eller endda i tømrerarbejde eller ethvert andet felt, hvor geometri spiller ind, eller når du beregner relative dimensioner eller afstande. Du kan multiplicere rødder, der har samme kraft (kraftrødder). Hvis radikaler ikke har den samme kraft, kan du redigere deres ligning, indtil de har. Hvis du vil vide, hvordan du multiplicerer rødder med eller uden koefficienter, skal du følge trinene nedenfor.
Trin
Metode 1 af 3: Multiplicering af rødder uden koefficienter

1. Sørg for, at rødderne har samme kraft. For at formere rødder ved hjælp af den grundlæggende metode, skal de have samme styrke. `Poten` er det lille skrevne tal til venstre for den øverste linje af rodsymbolet. Hvis ingen potens er angivet, har du at gøre med en kvadratrod (anden potens), og den kan ganges med andre kvadratrødder. Du kan gange rødder af forskellige magter sammen, men det er en avanceret metode og vil blive forklaret senere. Her er to eksempler på at gange rødder med de samme potenser:
- Eks. 1: √(18) x √(2) = ?
- Eks. 2: √(10) x √(5) = ?
- Eks. 3: √(3) x √(9) = ?

2. Gang tallene under radikalet. Så gange du tallene under det radikale tegn og lader det være der. Dette går sådan her:

3. Forenkle rødderne. Når du har ganget rødderne, er der en god chance for, at de kan forenkles til en perfekt kvadrat eller potens af to, eller de kan forenkles ved at finde en kvadrat som en faktor for det endelige produkt. Det gør du på følgende måde:
Metode 2 af 3: Multiplicer rødder med koefficienter

1. Multiplicer koefficienterne. Koefficienterne er tallene uden for radikalet. Hvis der ikke er angivet nogen koefficient, kan du betragte koefficienten som 1. Multiplicer koefficienterne sammen. Det gør du på følgende måde: Eks. 2: 4√(3) x 3√(6) = 12√( ? ) 4 x 3 = 12
- Eks. 1: 3√(2) x √(10) = 3√( ? )
- 3 x 1 = 3

2. Multiplicer tallene inden for rødderne. Når du har ganget koefficienterne, kan du begynde at gange tallene inde i rødderne. Det gør du på følgende måde:

3. Forenkle produktet. Så forenkler du tallene under rødderne ved at lede efter de perfekte kvadrater eller multipla af tallene under rødderne, der udgør perfekte kvadrater. Når du har forenklet disse udtryk, skal du gange deres tilsvarende koefficienter med. Det gør du på følgende måde:
Metode 3 af 3: Multiplicer forskellige magtrødder

1. Find potensernes LCF (Least Common Multiple). For at finde potensernes LCF skal du finde det mindste tal, der er deleligt med begge potenser. Find LCF for indekserne for følgende ligning: √(5) x √(2) = ?
- Indeksene er 3 og 2. 6 er LCF for disse to tal, fordi det er det mindste tal, der er deleligt med både 3 og 2. 6/3 = 2 og 6/2 = 3. For at gange rødderne skal begge potenser være 6.

2. Skriv hvert udtryk med den nye LCF som potens. Udtrykkene vil se sådan ud sammenlignet med deres nye kræfter:

3. Find det tal, som du skal gange hver af de oprindelige potenser med for at bestemme LCF. Med udtrykket √(5) skal din potens af 3 ganges med 2 for at få 6. Med udtrykket √(2) skal du gange potens 2 med 3 for at få 6.

4. Gør dette tal til eksponenten af tallet inden for kvadratroden. I den første ligning bliver 2 til potensen af 5. I den anden ligning bliver 3 til potensen af 2. Dette vil se sådan ud:

5. Multiplicer tallene inden for rødderne med deres eksponenter. Det gør du på følgende måde:

6. Placer disse tal under et radikal. Placer dem under et radikalt tegn og forbind dem med et multiplikationstegn. Sådan ser resultatet ud: √(8 x 25)

7. Formere sig. √(8 x 25) = √(200). Dette er det endelige svar. I nogle tilfælde kan du muligvis forenkle disse udtryk endnu mere - for eksempel hvis du kan finde et tal, der ganges seks gange med sig selv giver 200. Men det er ikke muligt, hvilket betyder, at udtrykket ikke kan forenkles yderligere.
Tips
- Hvis der er et plus- eller minustegn mellem et tal og radikalet, så er det ikke en koefficient - i så fald er det et separat udtryk og skal behandles separat fra radikalet. Hvis et radikal og et andet led er indesluttet i parentes -- for eksempel (2 + √5), så skal du behandle både 2 og √5 separat, når du udfører operationer inden for parentesen, men når du udfører operationer uden for parentesen, skal du betragte (2 + √5) som én helhed.
- Rodtegn er en anden måde at udtrykke brøkeksponenter på. Med andre ord er kvadratroden af et tal det samme som det tal hævet til 1/2-potensen, terningroden af ethvert tal er det samme som det tal hævet til 1/3-potensen, og så videre.
- EN "koefficient" er tallet (hvis der er et tal) umiddelbart før radikalet. Så i udtrykket 2√5 er 5 under radikalet og tallet 2 (uden for radikalet) er koefficienten. Når en rod og en koefficient er repræsenteret som en gruppe, betyder det, at roden og koefficienten skal ganges med hinanden, således som i eksemplet: 2 * √5.
Artikler om emnet "Gang gulerodsnumre sammen"
Оцените, пожалуйста статью
Populær