I denne ligning henviser . til N til normalkraften, m refererer til objektets masse og g til tyngdeaccelerationen. For et objekt på en flad overflade uden udefrakommende kræfter er normalkraften lig med objektets vægt. For at holde objektet i ro skal normalkraften være lig med tyngdekraften på objektet. Tyngdekraften er objektets vægt eller også massen gange tyngdeaccelerationen. Eksempel: Bestem normalkraften af en blok med en masse på 4.2 kg. 
Bemærk, at tyngdeaccelerationen på jordens overflade er en konstant: g = 9.8 m/s2 Eksempel: vægt = m * g = 4.2*9.8 = 41.16 
Eksempel: Normalkraften er 41.16 N. 

Denne værdi beregnes ofte med en lommeregner, fordi cosinus for hver vinkel er konstant for den vinkel, men du kan også beregne det i hånden. Eksempel: cos(45) = 0.71 
Bemærk, at tyngdeaccelerationen på jordens overflade er en konstant: g = 9.8 m/s2 Eksempel: vægt = m * g = 4.2*9.8 = 41.16 
Eksempel: N = m * g * cos(x) = 41.16*0.71 = 29.1 
Bemærk, at et objekt på en skråning har en normalkraft, der er mindre end objektets vægt. Eksempel: Normalkraften er 29.1 N. 

Bemærk, at tyngdeaccelerationen på jordens overflade er konstant: g = 9.8 m/s2 Eksempel: vægt = m * g = 4.2*9.8 = 41.16 
Eksempel: sin(30) = 0.5 
Eksempel: 0.5*20.9 = 10.45 
Eksempel: 10.45 + 41.16 = 51.61 
Eksempel: Normalkraften er 51.61 NR. 

Bemærk, at tyngdeaccelerationen på jordens overflade er en konstant: g = 9.8 m/s2 Eksempel: vægt = m * g = 4.2*9.8 = 41.16 
Eksempel: sin(50) = 0.77 
Eksempel: 0.77*20.9 = 16.01 
Eksempel: 41.16 – 16.01 = 25.15 
Eksempel: Normalkraften er 25.15 N. 

Begge sider af den oprindelige ligning blev divideret med μ, at bringe normalkraften til den ene side af ligningen og friktionskoefficienten og kinetisk friktion til den anden side. Eksempel: Bestem normalkraften af en blok, når friktionskoefficienten er 0.4 og selve graden af kinetisk friktion er 40 N. 
Eksempel: N = f / = 40 / 0.4 = 100 
Eksempel: Normalkraften er 100.0 N.
Beregning af normalkraften
Indhold
Normalkraften er mængden af kraft, der skal til for at modvirke andre kræfter i en given situation. Den bedste måde at bestemme dette på afhænger af de forhold et objekt er i, og de variabler, du har dataene til. Fortsæt med at læse for at lære mere.
Trin
Metode 1 af 5: Normal kraft i hvile

1. Forstå hvad normal kraft henviser. Normalkraft refererer til mængden af kraft, der kræves for at modvirke tyngdekraften.
- Forestil dig en blok liggende på et bord. Tyngdekraften trækker blokken mod jorden, men der er åbenbart en kraft, der forhindrer blokken i at ramle gennem bordet og ramme jorden. Den kraft, der er ansvarlig for at annullere tyngdekraften, er normal kraft.

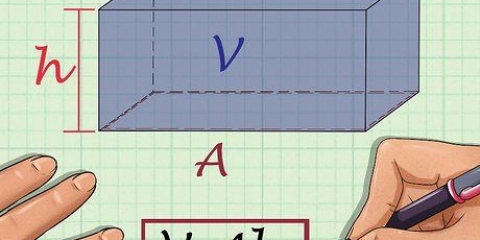
2. Kend ligningen for normalkraften af et objekt i hvile. Når du beregner normalkraften af et objekt i hvile på en flad overflade, skal du bruge formlen: N = m * g

3. Multiplicer objektets masse med tyngdeaccelerationen. Herved kender du genstandens vægt, som i sidste ende er lig med genstandens normalkraft i hvile.

4. Skriv dit svar ned. Det forrige trin burde have løst hele problemet og give dig svaret nu.
Metode 2 af 5: Normal kraft på en skråning

1. Brug den rigtige ligning. For at bestemme normalkraften af et objekt i en vinkel, skal du bruge følgende formel: N = m * g * cos(x)
- I denne ligning henviser . til N til normalkraften, m refererer til objektets masse, g henviser til tyngdeaccelerationen, og x refererer til vinklen eller hældningen.
- Eksempel: Bestem normalkraften af en blok med en masse på 4.2 kg, som er placeret på en hylde med 45 graders hældning.

2. Bestem vinklens cosinus. Cosinus af en vinkel er lig med sinus af komplementær vinkel eller tilstødende side divideret med hypotenusen af trekanten dannet af hældningen.

3. Bestem vægten af objektet. Vægten af et objekt er lig med massen af det objekt ganget med tyngdeaccelerationen.

4. Multiplicer begge værdier sammen. For at bestemme normalkraften skal du gange vægten af objektet med cosinus af hældningsvinklen.

5. Skriv dit svar ned. Det forrige trin fuldender problemet og giver dig svaret.
Metode 3 af 5: Normalkraft med en ekstern nedadgående kraft

1. Brug den rigtige ligning. For at beregne normalkraften af et objekt i hvile, hvor en ekstern nedadgående kraft påføres det objekt, skal du bruge ligningen: N = m * g + F * sin(x)`
- N henviser til normalkraften, m refererer til objektets masse, g refererer til tyngdeaccelerationen, f henviser til den ydre kraft, og x refererer til vinklen mellem objektet og retningen af den ydre kraft.
- Eksempel: Bestem normalkraften af en blok med en masse på 4.2 kg, hvor en person udøver en nedadgående kraft på 20.Påfør 9 N på blokken i en 30 graders vinkel.

2. Bestem vægten af objektet. Vægten af et objekt er lig med objektets masse ganget med tyngdeaccelerationen.

3. Bestem vinklens sinus. En vinkels sinus beregnes ved at dividere længden af trekantens side modsat vinklen med trekantens hypotenus.

4. Gang sinus med den ydre kraft. Den ydre kraft refererer i dette tilfælde til den nedadgående kraft på objektet.

5. Tilføj denne værdi til vægten. Dette giver dig den normale kraft.

6. Skriv dit svar ned. Bemærk, at for et objekt i hvile, hvor en ekstern nedadgående kraft påføres objektet, vil normalkraften være større end objektets vægt.
Metode 4 af 5: Normalkraft med en ekstern opadgående kraft

1. Brug den rigtige ligning. For at beregne normalkraften af et objekt i hvile, hvor en ekstern, opadgående kraft udøves på det objekt, skal du bruge ligningen: N = m * g - F * sin(x)`
- N henviser til normalkraften, m refererer til objektets masse, g refererer til tyngdeaccelerationen, f henviser til den ydre kraft og x refererer til vinklen mellem objektet og retningen af den ydre kraft.
- Eksempel: Bestem normalkraften af en blok med en masse på 4.2 kg, hvor en person løfter blokken i en vinkel på 50 grader og med en kraft på 20.9 NEJ.

2. Bestem vægten af objektet. Vægten af et objekt er lig med objektets masse ganget med gravitationsaccelerationen.

3. Bestem vinklens sinus. En vinkels sinus beregnes ved at dividere længden af trekantens side modsat vinklen med trekantens hypotenus.

4. Gang sinus med den ydre kraft. Den ydre kraft refererer til den flydekraft, der udøves på objektet, i dette tilfælde.

5. Træk denne værdi fra vægten. Med dette har du fundet den normale kraft på arbejde.

6. Skriv dit svar. Bemærk, at for et objekt i hvile, hvor en ekstern opadgående kraft påføres objektet, vil normalkraften være mindre end objektets vægt.
Metode 5 af 5: Normal kraft og friktion

1. Lær standardligningen for kinetisk friktion. Kinetisk friktion, eller friktionen på et objekt i bevægelse, er lig med friktionskoefficienten ganget med en genstands normalkraft. I en sammenligning ser det sådan ud: f = * N
- I denne ligning er f for friktion, den μ refererer til friktionskoefficienten, ogN refererer til objektets normalkraft.
- Det "friktionskoefficient" er forholdet mellem friktionsmodstanden og normalkraften, som er ansvarlig for komprimeringen af de to modstående flader.

2. Omarranger ligningen for at isolere normalkraften. Hvis du har en værdi for en genstands kinetiske friktion, kan du ud over objektets friktionskoefficient beregne normalkraften ved hjælp af formlen: N = f /

3. Divider den kinetiske friktion med friktionskoefficienten. Dette er stort set alt, hvad du skal gøre for at bestemme normalkraften.

4. Skriv dit svar. Hvis det ønskes, kan du kontrollere dit svar ved at indtaste det i den oprindelige ligning for kinetisk friktion. Ellers har du nu løst problemet.
Fornødenheder
- Blyant
- Papir
- Lommeregner
Artikler om emnet "Beregning af normalkraften"
Оцените, пожалуйста статью
Populær