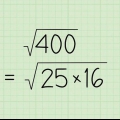Afrunding af tal

Indhold

Trin
Tips
Advarsler

Afrunding gør, at tal har færre decimaler. Selvom afrundede tal er mindre nøjagtige end uafrundede tal, foretrækkes de i mange tilfælde. Afhængigt af situationen kan det være nødvendigt at afrunde decimaler eller heltal. Hvis du gerne vil lære at afrunde tal, skal du følge disse trin.

Trin

Metode 1 af 3: Afrunding af decimaler

1. Bestem antallet af decimaler for cifrene efter decimaltegnet, hvortil du skal afrunde tallet. Dette kan bestemmes af din lærer, eller du kan udlede det ud fra konteksten og den slags tal, du har med at gøre med. For eksempel, når det kommer til penge, vil du højst sandsynligt afrunde til hundrededelen eller til centen, mens du med en vægt skal afrunde til gram.

Jo mindre nøjagtigt tallet skal være, jo færre cifre efter decimaltegnet.
Jo mere nøjagtigt, jo flere cifre efter decimaltegnet.

2. Bestem antallet af cifre efter decimaltegnet. er nummeret 10,7659 givet, og du vil afrunde det til en tusindedel, så vil der være 3 cifre efter decimalkommaet. En anden tilgang er, at du afrunder tallet til 5 signifikante cifre. Men læg først mærke til 5 af nummeret.

3. Find tallet umiddelbart til højre for tallet, der skal afrundes (de 5). Det er tallet 9. Dette tal afgør, om 5 er rundet op eller ned.

4. Afrund det ciffer, der skal afrundes (det relevante ciffer), hvis cifferet til højre er 5, 6, 7, 8 eller 9. Dette kaldes at runde op, fordi det tal du runder til er større end det tal der skal rundes op. Den relevante figur 5, bliver nu 6. Alle cifre til venstre for dette ciffer forbliver de samme, og cifrene til højre forsvinder (de betyder ikke noget længere, bare sæt dem lig med nul). Altså nummeret 10,7659 bliver lig med efter afrunding til nærmeste tusindedel 10,766.

Selvom 5`eren er i midten af tallene 1-9, er tallet 5 har brug for et andet tal for at bestemme, hvordan det skal rundes op. Selvom dine lærere ikke altid anvender dette, når de bedømmer dig!

5. Afrund et ciffer ned, hvis cifferet til højre for det er 0, 1, 2, 3 eller 4. Det betyder for den relevante figur, at den simpelthen forbliver den samme, selvom det kaldes afrunding nedad. Du kan aldrig ændre et tal til et lavere tal. Har du f.eks. nummeret 10,7653, så ville du runde dette ned til 10,765 fordi karakteren 3 på højre side af 5 er mindre end 5.

Ved at lade alt være det samme og sætte tallene til højre for det afrundede ciffer til nul, bliver det endelige tal mindre end originalen.

Metode 2 af 3: Afrunding af heltal

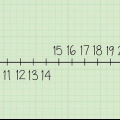
1. Afrund et tal til de næste ti. For at gøre dette skal du se på tallet til højre for de ti. Tieren er det andet ciffer, set fra højre mod venstre, i et tal. (Tag 12, så er 1 de ti.) Så, hvis det tal er mellem 0-4, lad cifferet afrunde uændret; hvis det er mellem 5-9, rund dette tal 1 op. Her er nogle eksempler:

12 --> 10
114 --> 110
57 --> 60
1.334 --> 1330
1.488 --> 1490
97--> 100

2. Afrund et tal til det næste hundrede. Følg samme protokol som før med de ti. Tjek hundrede, det tredje ciffer i et tal, til venstre for ti. (I nummer 1.234, 2 er hundrede). Brug derefter tallet til højre for hundrede, ti, til at bestemme, om der skal rundes op eller ned, med tallene efter det lig nul. Her er nogle eksempler:

7.891 -- > 7.900

15.753 --> 15.800

99. 961 --> 100.000

3.350 --> 3.300

450 --> 500

3. Afrund et tal til næste tusind. De samme regler gælder her igen. Find tusinde og tjek derefter hundrede før afrunding. Hvis tallet er mellem 0-4, rund ned, og hvis det er mellem 5-9, rund op. Her er et par flere eksempler:

8.800 --> 9.000

1.015 --> 1.000

12.450 --> 12.000

333.878 --> 334.000

400.400 --> 400.000

Metode 3 af 3: Afrunding af tal til signifikante cifre

1. Prøv at forstå, hvad et betydeligt tal er. Betragt et væsentligt ciffer som et "interessant" eller a "vigtig" nummer, der giver nyttige oplysninger om et nummer. Det betyder, at alle nuller til højre for heltal eller til venstre for decimaler kan udelades, da de bare fylder rummet. For at finde antallet af signifikante cifre i et tal skal du blot tælle antallet af cifre fra venstre mod højre. Her er et par eksempler:

1.239 har 4 signifikante cifre
134,9 har 4 signifikante cifre
0,0165 har 3 signifikante cifre

2. Afrund et tal til et antal signifikante cifre. Dette afhænger af den opgave, du arbejder med. Hvis du f.eks. afrunder et tal til to betydende cifre, skal du prøve at genkende det andet betydende ciffer i tallet og derefter bruge tallet til højre for at afgøre, om du skal runde op eller ned. Her er nogle eksempler:

1,239 afrundet til 3 signifikante cifre er 1,24. Dette er korrekt, fordi cifferet til højre for det tredje ciffer (3) er et 9 (mere end 5).

134,9 afrundet til 1 signifikant ciffer er 100. Dette er korrekt, fordi cifferet til højre for hundrede (1) er et 3 (mindre end 5).

0.0165 afrundet til 2 signifikante cifre er 0.017. Dette er korrekt, fordi det andet signifikante ciffer er lig med 6, og tallet til højre er et 5, så rundes op.

3. Afrund til det korrekte antal signifikante tal ved tilføjelse. For at gøre dette er det nødvendigt først at lægge de givne tal sammen. Find derefter tallet med det mindste antal signifikante cifre, og afrund dit svar til det tal. Sådan fungerer det:

13.214 + 234.6 + 7.0350 + 6.38=261.2290

Bemærk, at det andet tal, 234,6, kun er nøjagtigt til en tiendedel og har fire signifikante cifre.

Afrund svaret, så svaret har samme nøjagtighed, dvs. til nærmeste tiendedel eller til en decimal. 261,2290 bliver så til 261,2.

4. Afrund til det korrekte antal signifikante cifre, når du multiplicerer. Gang først alle givne tal. Kontroller derefter, hvilket af tallene der er afrundet til det mindste antal signifikante cifre. Afrund til sidst svaret med samme grad af nøjagtighed som det tal. Sådan fungerer det:

16,235 × 0,217 × 5=17,614975

Bemærk, at tallet 5 kun har ét signifikant ciffer. Det betyder, at det endelige svar kun kan have ét signifikant ciffer.

17.614975 afrundet til et signifikant ciffer bliver så 20.

Tips

Det er almindeligt at udelade nullerne til højre for en decimal efter afrunding. Nuller til højre for en decimal ændrer ikke værdien af tallet. Derfor bør de udelades. Dette gælder ikke for nuller til venstre for (før) en decimal.
Når du har fundet det relevante tal at runde af, skal du understrege det. Dette sikrer, at der ikke er nogen forvirring om det tal, du skal afrunde, og det tal, som det relevante tal er afrundet til.

Advarsler

Sørg for, at du er fortrolig med terminologien. Forskellen mellem tiere og tiendedele, hundrededele og hundrededele, decimaler, decimaler, betydning osv...