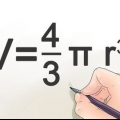Beregning af effektfaktorkorrektion: 8 trin (med billeder)

Indhold

Trin
Advarsler
Fornødenheder

Gennem effektfaktorkorrektionen kan du beregne den tilsyneladende effekt, effekt, reaktiv effekt og fasevinklen. Overvej ligningen for en retvinklet trekant. For at beregne en vinkel skal du vide, hvad cosinus, sinus og tangent er. Du skal også bruge Pythagoras sætning (c² = a² + b² ) til at beregne dimensionerne af trekantens sider. Du skal også vide, hvilke enheder hver type evner har. Tilsyneladende effekt måles i Volt-Ampère. Effekt måles i watt, og reaktiv effekt er udtrykt i Volt-Amp Reactive (VAR) enheder. Der er flere ligninger til at beregne disse, og alle vil blive dækket i denne artikel. Du har nu grundlaget for det, du forsøger at beregne.

Trin

1. Beregn impedansen. (Lad som om impedansen er på samme sted som den tilsyneladende effekt på billedet ovenfor). For at bestemme impedansen bruger du Pythagoras sætning, c² = √ (a² + b²).

Billede med titlen Beregn effektfaktorkorrektion Trin 2

2. Således er den samlede impedans (repræsenteret som `Z`) lig med potensen i anden, plus den reaktive effekt i anden, så tager du kvadratroden af svaret.

(Z = √(60² + 60²)). Så hvis du indtaster det i din videnskabelige lommeregner, er svaret 84,85Ω. (Z = 84,85Ω).

Billede med titlen Beregn effektfaktorkorrektion Trin 3

3. Bestem fasevinklen. Så nu har du hypotenusen, som er impedansen. Du har også en tilstødende side, kraften, og du har den modsatte side, den reaktive effekt. Så for at finde vinklen kan du bruge en af de tidligere nævnte formler. For eksempel bruger vi tangentformlen, dvs. den modsatte side divideret med den tilstødende (reaktiv/potens).

Du har så en ligning som: (60/60 = 1)

Billede med titlen Beregn effektfaktorkorrektion Trin 4

4. Tag den reciproke af tangenten for fasevinklen. Den omvendte tangent er en knap på din lommeregner. Så tag nu den inverse tangens af ligningen i det foregående trin, og du får fasevinklen. Din ligning skulle se sådan ud: tan ‾ ¹ (1) = fasevinkel. dit svar bliver så 45°.

Billede med titlen Beregn effektfaktorkorrektion Trin 5

5. Beregn den samlede strøm (Ampere). Strømmen vises også som et `A` i enheden Ampere. Formlen der bruges til at beregne strømmen er spændingen divideret med impedansen, så dette er: 120V/84.85Ω. Du har nu et svar på omkring 1.141A. (120V/84,84Ω = 1,141A).

Billede med titlen Beregn effektfaktorkorrektion Trin 6

6. Du skal nu beregne den tilsyneladende effekt, der vises som `S`. Du behøver ikke bruge Pythagoras sætning til at beregne tilsyneladende styrke, fordi din hypotenus anses for din impedans. Husk, at tilsyneladende effekt bruger enheden Volt-Ampere: vi kan beregne den tilsyneladende effekt ved hjælp af formlen: Spænding i anden række divideret med total impedans. Din ligning skulle se sådan ud: 120V²/84.85Ω. Nu skulle du få et svar som: 169.71VA. (120²/84,85 = 169,71).

Billede med titlen Beregn effektfaktorkorrektion Trin 7

7. Du skal nu beregne den effekt, der vises som `P`. For at beregne effekten skal du bruge strømmen, som du gjorde i trin fire. Effekten er i watt og beregnes ved at gange strømmen i anden kvadrat (1,141²) med modstanden (60Ω) i dit kredsløb. Du skulle få et svar på 78,11 watt. Ligningen skal se sådan ud: 1,141² x 60 = 78,11.

Billede med titlen Beregn effektfaktorkorrektion Trin 8

8. Beregn effekt eller effektfaktor! For at beregne effektfaktoren skal du bruge følgende information: Watt og Volt-Ampere. Du har beregnet disse oplysninger i de foregående trin. Effekten er lig med 78,11W og Volt-Ampère er 169,71VA. Formlen for effektfaktoren, også repræsenteret som Pf, er watt divideret med Volt-Amp. Din ligning ser nu sådan ud: 78.11/169.71 = 0.460.

Dette kan også udtrykkes i procent, så man ganger 0,460 med 100, hvilket giver en effektfaktor på 46 %.

Advarsler

Når du beregner impedans, bruger du den inverse tangentfunktion og ikke kun den almindelige tangentfunktion på din lommeregner. Ellers får du en forkert fasevinkel.
Dette var blot et meget simpelt eksempel på beregning af en fasevinkel og effektfaktor. Der er meget mere komplicerede kredsløb, inklusive kapacitanseffekt og højere modstande og impedans.