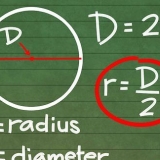
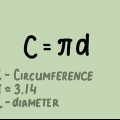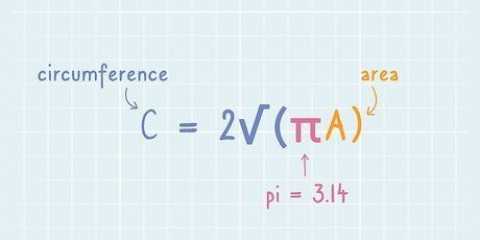Læg en tråd rundt om omkredsen, så præcist som muligt. Marker ledningen, når cirklen er færdig, og mål derefter længden af ledningen med en lineal. 




π=3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11 *12) - 4/(12*13*14) ... Du anvender denne formel ved først at tage 2 og derefter skiftevis addere og subtrahere brøker, med tælleren 4 og nævneren produktet af 3 på hinanden følgende heltal, der stiger med hver ny iteration. Hver fortløbende brøk starter med en række heltal, hvor det første tal i serien er det sidste tal i den forrige brøk (i den foregående brøk). Selvom du kun gør dette få gange, vil du snart komme tæt på pi. 


pi=2 *(Arcsin(sqrt(1 - x^2))) + abs(Arcsin(x)). Arcsin refererer til en invers sinus i radianer Sqrt er en forkortelse for kvadratroden af Abs er en forkortelse for absolut værdi x^2 er en vis potens, i dette tilfælde x i anden.
Udregn pi
Indhold
Pi (π) er et af de vigtigste og mest fascinerende tal i matematik. Simpelthen vist som 3.14, bruges som en konstant til at beregne omkredsen af en cirkel ved hjælp af dens radius eller diameter. Det er også et irrationelt tal, hvilket betyder, at du kan beregne det til et uendeligt antal decimaler uden nogensinde at støde på et gentaget mønster. Dette gør det svært, men ikke umuligt, at arbejde præcist.
Trin
Metode 1 af 5: Beregning af Pi ved hjælp af en cirkel

1. Sørg for at bruge en perfekt cirkel. Denne metode fungerer ikke med en ellipse, ellipse eller noget andet end en rigtig cirkel. En cirkel er defineret som alle punkter i et plan, der er lige langt fra et givet centralt punkt. For eksempel er låg på et syltetøjsglas et fint værktøj at bruge til denne øvelse. Du kan groft beregne en værdi af Pi med dette. Selv den tyndeste, skarpeste blyant er stadig enorm sammenlignet med den nøjagtighed, der kræves til en nøjagtig beregning af tallet Pi.

2. Mål cirklens omkreds så nøjagtigt som muligt. Omkredsen er længden af hele cirklens omkreds. Da dette går rundt, kan det være lidt vanskeligt at måle (det er derfor Pi er så vigtig).

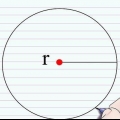
3. Mål diameteren af cirklen. Diameteren er længden af tværsnittet af en cirkel gennem midten af cirklen.

4. Brug formlen. Omkredsen af en cirkel kan findes med formlen C=π*d=2*π*r. Så pi er lig med omkredsen af cirklen divideret med diameteren. Indtast dine tal i en lommeregner: resultatet skal være omkring 3.skal være 14.

5. For et mere præcist resultat skal du gentage denne proces i flere cirkler og derefter gennemsnittet resultaterne. Dine aflæsninger er måske ikke perfekte, når det kommer til en individuel læsning, men over tid burde gennemsnittet være en rigtig god tilnærmelse af Pi.
Metode 2 af 5: Beregning af Pi ved hjælp af Infinite Series

1. Gør brug af Gregory-Leibniz-serien. Matematikere har fundet flere matematiske sekvenser, der, hvis de følges til det uendelige, kan beregne Pi til et enormt antal decimaler. Nogle af disse sekvenser er så komplekse, at det kræver supercomputere at behandle dem. En af de enkleste er dog Gregory-Leibniz-serien. Måske ikke særlig effektiv, men det giver et mere nøjagtigt tal for pi med hver iteration, og ender til sidst på 5 decimaler efter 500.000 gentagelser. Her er formlen, der skal bruges.
- π=(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
- Tag 4 og træk 4 divideret med 3 fra dette. Tilføj derefter 4 divideret med 5. Træk så 4 divideret med 7 igen. Fortsæt med at gentage dette mønster med en tæller 4 og et fortløbende ulige tal i nævneren. Jo mere du gør dette, jo tættere kommer du på pi.

2. Udnyt Nilakantha-serierne. Dette er en anden uendelig serie, der giver dig mulighed for at beregne pi og er ikke svær at forstå. Selvom det er lidt mere kompliceret, kan du beregne pi meget hurtigere med det end med Leibniz-formlen.
Metode 3 af 5: Beregning af Pi ved hjælp af Buffons nåleproblem

1. Prøv følgende eksperiment for at beregne pi ved at kaste med hotdogs. Pi indgår også i tankeeksperimentet kaldet Buffon`s Needle Problem, som forsøger at bestemme sandsynligheden for, at tilfældigt kastede, lignende formede genstande vil lande mellem eller på en række parallelle linjer på gulvet. Det viser sig, at hvis afstanden mellem linjerne er lig med længden af de kastede objekter, så kan antallet af gange objekterne lander på en linje efter mange kast bruges til at beregne pi.
- Forskere og matematikere har endnu ikke opdaget en måde at beregne pi nøjagtigt på, fordi de endnu ikke har fundet et materiale så tyndt, at man kan udføre nøjagtige beregninger med det.
Metode 4 af 5: Beregning af Pi med en grænse

1. Vælg et stort antal. Jo større tal, jo mere nøjagtig vil din beregning være.

2. Brug tallet, som vi kalder x, i denne formel til at beregne pi:x *sin (180/x). For at dette skal virke, skal du sørge for, at din lommeregner er indstillet til grader. Grunden til, at dette kaldes en grænse, er, at resultatet er `begrænset` til pi. Når du øger dit tal x, kommer resultatet tættere og tættere på værdien af pi.
Metode 5 af 5: Arcsinus og invers sinusfunktion
1. Vælg et tal mellem -1 og 1. Dette skyldes, at arcsine ikke er defineret for tal større end 1 eller mindre end -1.
2. Brug tallet i følgende formel, og resultatet er nogenlunde lig med pi.
Tips
- At beregne pi er sjovt og udfordrende, men hvis du beregner for mange decimaler, vil det ikke være til meget nytte .Astronomer siger, at det ikke kræver mere end 39 decimaler for tallet pi at udføre meget nøjagtige beregninger.
Оцените, пожалуйста статью
Populær