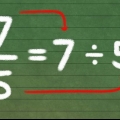Konverter et decimaltal til binært ieee 754 Format: 11 trin (med billeder)

I modsætning til mennesker bruger computere ikke decimaltalsystemet. De bruger et binært eller binært talsystem med to mulige cifre, 0 og 1. Så tal er skrevet meget anderledes i IEEE 754 (en IEEE-standard til at repræsentere binære tal med et flydende komma) end i det traditionelle decimalsystem, vi er vant til. I denne artikel lærer du, hvordan du skriver et tal i enten enkelt eller dobbelt præcision i henhold til IEEE 754. Til denne metode skal du vide, hvordan du konverterer tal til binær form. Hvis du ikke ved, hvordan du gør dette, så kan du lære det gennem artiklen Konverter binær til decimal at studere.

Trin

1. Vælg enkelt eller dobbelt præcision. Når du skriver et tal med enkelt eller dobbelt præcision, vil trinene til en vellykket konvertering være de samme for begge. Den eneste ændring sker ved konvertering af eksponenten og mantissen.

Først skal vi forstå, hvad enkelt præcision betyder. I floating point view betragtes ethvert tal (0 eller 1) som en `bit`. Derfor har en enkelt præcision i alt 32 bit fordelt på tre forskellige emner. Disse emner består af et tegn (1 bit), en eksponent (8 bit) og en mantisse eller brøk (23 bit).
Dobbelt præcision har på den anden side den samme opsætning og de samme tre dele som enkelt præcision - den eneste forskel er, at det vil være et større og mere nøjagtigt tal. I dette tilfælde vil tegnet være 1 bit, eksponenten 11 bit og mantissen 52 bit.
I dette eksempel skal vi konvertere tallet 85.125 til enkeltpræcision i henhold til IEEE 754.

2. Adskil tallet før og efter decimaltegnet. Tag det tal, du vil konvertere, og bryd tallet ad, så du står tilbage med et helt tal og et decimaltal. I dette eksempel antager vi tallet 85.125. Du kan adskille dette i hele tallet 85 og decimaltallet 0,125.

3. Konverter hele tallet til et binært tal. Dette vil være 85 af 85,125, som bliver 1010101, når det konverteres til binær.

4. Konverter decimaldelen til et binært tal. Dette er så 0,125 af 85,125, som bliver 0,001 i binær notation.

5. Kombiner de to dele af tallet konverteret til binære tal. Tallet 85 er binært f.eks. 1010101 og decimaldelen 0,125 er binært 0,001. Hvis du kombinerer dem med en decimal, får du 1010101.001 som endeligt svar.

6. Konverter binært tal til videnskabelig binær notation. Du kan konvertere tallet til videnskabelig binær notation ved at flytte decimaltegnet til venstre, indtil det er til højre for den første bit. Disse tal er normaliserede, hvilket betyder, at den førende bit altid vil være 1. Hvad angår eksponenten, er antallet af gange, du flytter decimalen, eksponenten i videnskabelig binær notation.

Husk, at flytning af decimalen til venstre giver en positiv eksponent, mens flytning af decimalen til højre giver en negativ eksponent.

I vores eksempel skal du flytte decimalen seks gange for at få den til højre for den første bit. Den resulterende notation bliver så

01, 010101001 * 2 6

${displaystyle 01.010101001*2^{6}}$ . Dette nummer vil blive brugt i de følgende trin.

7. Bestem tegnet for tallet og vis det i binær notation. Du vil nu afgøre, om det oprindelige tal er positivt eller negativt. Hvis tallet er positivt, skal du skrive den bit som 0, og hvis det er negativt, som 1. Da det oprindelige tal er 85,125 positivt, skal du skrive den bit som 0. Dette er nu den første bit af de i alt 32 bits i din enkeltpræcisionsrepræsentation i henhold til IEEE 754.

8. Bestem eksponenten ud fra præcisionen. Der er en fast bias for både enkelt og dobbelt præcision. Forspændingen af den enkelte præcisionseksponent er 127, hvilket betyder, at vi skal tilføje den tidligere fundne binære eksponent. Så den eksponent du skal bruge er 127 + 6 = 133.

Dobbelt præcision, som navnet antyder, er mere nøjagtig og kan indeholde større tal. Derfor bias af eksponenten 1023. De samme trin, der bruges til enkelt præcision, gælder her, så den eksponent, du kan bruge til at bestemme dobbelt præcision, er 1029.

9. Konverter eksponenten til binær. Når du har bestemt din endelige eksponent, skal du konvertere den til binær, så den kan bruges i IEEE 754-konverteringen. I eksemplet kan du konvertere de 133 du fandt i sidste trin til 10000101.

10. Bestem mantissen. Mantisse-aspektet eller den tredje del af IEEE 754-konverteringen er resten af tallet efter decimalen for videnskabelig binær notation. Du udelader bare 1`et foran og kopierer decimaldelen af tallet ganget med to. Ingen binær konvertering påkrævet! I eksemplet bliver mantissen 010101001 af

01, 010101001 * 2 6

${displaystyle 01.010101001*2^{6}}$ .

11. Til sidst kombinerer du tre dele til ét tal.

Til sidst kombinerer du alt, hvad vi hidtil har beregnet i din konvertering. Tallet starter først med et 0 eller 1, som du bestemte i trin 7 baseret på tegnet. I eksemplet starter du med 0.

Så har du eksponenten, som du bestemte i trin 9. I eksemplet er eksponenten 10000101.

Så kommer mantissen, den tredje og sidste del af konverteringen. Du udledte dette tidligere, da du tog decimaldelen af den binære konvertering. I eksemplet er mantissen 010101001.

Til sidst kombinerer du disse tal med hinanden. Rækkefølgen er fortegn-eksponent-mantisse. Efter at have forbundet disse tre binære tal, skal du udfylde resten af mantissen med nuller.

For eksempel, hvis 85.125 konverteres til det binære IEEE 754-format, er løsningen 0 10000101 01010100100000000000000.