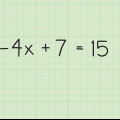Løsning af magiske firkanter

Indhold

Trin
Tips
Fornødenheder

Magiske firkanter er kun vokset i popularitet siden opkomsten af matematikbaserede spil som Sudoku. Et magisk kvadrat er et arrangement af tal i et kvadrat på en sådan måde, at summen af hver række, søjle og diagonal er et konstant tal, den såkaldte magiske konstant. Denne artikel vil forklare, hvordan man løser enhver form for magisk firkant, det være sig et ulige, enkelt lige eller dobbelt lige felt.

Trin

Metode 1 af 3: Løsning af en ulige magisk firkant

1. Beregn den magiske konstant. Du kan finde dette tal ved hjælp af en simpel matematisk formel, hvor n = antallet af rækker eller kolonner i din magiske firkant. Så for eksempel i en 3x3 magisk firkant, n = 3. Den magiske konstant = [n * (n2 + 1)] / 2. Så i eksemplet med 3x3 kvadratet:

sum = [3 * (32 + 1)] / 2
sum = [3 * (9 + 1)] / 2
sum = (3 * 10) / 2
sum = 30/2
Den magiske konstant for et 3x3 kvadrat er 30/2 eller 15.
Alle rækker, kolonner og diagonaler har dette tal som sum.

Billede med titlen Løs en magisk firkant Trin 2

2. Placer nummer 1 i den midterste boks i den øverste række. Dette er altid det punkt, hvor du starter, hvis dit magiske sidekvadrat har et ulige antal sider, uanset hvor stort eller lille det tal er. Så hvis du har en firkant på 3x3, skal du sætte tallet 1 i boks 2; i en 15x15 firkant skal du placere tallet 1 i boks 8.

Billede med titlen Løs en magisk firkant Trin 3

3. Udfyld de resterende tal i et én-til-højre mønster. Du udfylder altid tallene efter en række (1, 2, 3, 4 osv.).) ved at gå en række op og derefter en kolonne til højre. Du bemærker straks, at for at placere tallet 2 ender du over den øverste række, uden for den magiske firkant. Det er okay - selvom du altid går en-op-en-til-højre-metoden, er der tre undtagelser, der også følger et forudsigeligt mønster:

Hvis bevægelsen fører dig til en "kasse" over den magiske firkant, skal du blive i boksens kolonne, men placere tallet i den nederste række af den kolonne.

Hvis bevægelsen fører dig til en boks til højre for den magiske firkant, skal du blive i den række, men placere tallet i kolonnen i den række, yderst til venstre for firkanten.

Hvis bevægelsen fører dig til et felt, der allerede har et nummer, skal du gå tilbage til det forrige felt, der blev udfyldt, og placere det næste tal direkte over det.

Metode 2 af 3: Løsning af en simpel lige magisk firkant

Billede med titlen Løs en magisk firkant Trin 4

1. Forstå, hvad et simpelt lige kvadrat er. Alle ved, at et lige tal er deleligt med 2, men med magiske kvadrater er der forskellige metoder til at løse enkelte og dobbelte lige kvadrater.

Et simpelt lige kvadrat har et antal kvadrater pr. side, der er deleligt med 2, men ikke med 4.
Den mindste enkelt magiske firkant er 6x6, fordi 2x2 magiske firkanter ikke kan laves.

Billede med titlen Løs en magisk firkant Trin 5

2. Beregn den magiske konstant. Brug samme metode, som du ville gøre med ulige magiske kvadrater: den magiske konstant = [n * (n2 + 1)] / 2, hvor n = antallet af kvadrater pr. side. Så i eksemplet med en 6x6 kvadrat:

sum = [6 * (62 + 1)] / 2

sum = [6 * (36 + 1)] / 2

sum = (6 * 37) / 2

sum = 222/2

Den magiske konstant for et 6x6 kvadrat er 222/2 eller 111.

Alle rækker, kolonner og diagonaler skal lægges sammen for at give dette tal.

Billede med titlen Løs en magisk firkant Trin 6

3. Opdel den magiske firkant i fire lige store kvadranter . Mærk dem A (øverst til venstre), C (øverst til højre), D (nederst til venstre) og B (nederst til højre). For at bestemme, hvor stor hver firkant skal være, skal du dele antallet af felter i hver række eller kolonne i to.

Så for hver 6x6 kvadrat bliver hver kvadrant en 3x3 kvadrat.

Billede med titlen Løs en magisk firkant Trin 7

4. Tildel en række tal til hver kvadrant. Kvadrant A får en fjerdedel af tallene; Kvadrant B andet kvartal; Kvadrant C tredje kvartal og kvadrant D sidste fjerdedel af det samlede talområde af en 6x6 magisk firkant.

I eksemplet med en 6x6 kvadrat løses kvadrant A med tallene fra 1-9; kvadrant B med dem på 10-18; Kvadrant C med 19-27 og kvadrant D med 28-36.

Billede med titlen Løs en magisk firkant Trin 8

5. Løs hver kvadrant ved hjælp af den magiske kvadratmetode med et ulige antal felter pr. side. Kvadrant A er let at udfylde, da den starter med tallet 1, som magiske firkanter normalt gør. Kvadranter B-D starter dog med ulige tal - 10, 19 og 28, som for vores eksempel.

Behandl det første tal i hver kvadrant, som om det var et. Placer den i den midterste boks på den øverste række af hver kvadrant.

Behandl hver kvadrant som en lille magisk firkant. Selvom boksen er tilgængelig i en tilstødende kvadrant, ignorer den og hop til `undtagelsesreglen`, der passer til denne situation.

Billede med titlen Løs en magisk firkant Trin 9

6. Lav markørerne A og D. Hvis du har prøvet at tilføje kolonner, rækker og diagonaler med det samme, har du bemærket, at de ikke lægger op til den magiske konstant. Du bliver nødt til at bytte nogle kasser i den øverste venstre og nederste venstre kvadranter for at fuldende din magiske firkant. Vi kalder disse områder Marker A og Marker D.

Brug en blyant til at markere alle firkanterne i den øverste række, indtil du når den midterste boks i kvadrant A. Så i en 6x6 firkant markerer du boks 1 (med tallet 8), men i en 10x10 firkant markerer du kasse 1 og 2 (med tallet 17 og 24, henholdsvis).

Marker en firkant ved hjælp af de felter, du lige har markeret som den øverste række. Hvis du kun har markeret én boks, vil din firkant ikke bestå af mere end én boks. Vi kalder dette Mærkning A-1.

Så i en 10x10 magisk firkant består markør A-1 af boks 1 og 2 i række 1 og 2, hvilket skaber en 2x2 firkant i øverste venstre kvadrant.

I rækken umiddelbart under markør A-1 springer du over tallet i den første kolonne, og markerer så mange felter fra side til side, som du har angivet i markør A-1. Vi kalder denne midterste række Markering A-2.

Valg A-3 er en boks, der ligner A-1, men placeret i det nederste venstre hjørne af kvadranten.

Udvalg A-1, A-2 og A-3 danner sammen markør A.

Gentag denne proces i kvadrant D, og skab et identisk markørområde, markør D.

Billede med titlen Løs en magisk firkant Trin 10

7. Skift markører A og D. Dette er en 1-til-1 udveksling. Flyt boksene mellem kvadrant A og kvadrant D uden at ændre rækkefølgen. Når du har gjort dette, skal alle rækker, kolonner og diagonaler i dit magiske kvadrat have den tidligere beregnede magiske konstant som deres sum.

Billede med titlen MagicSquare14x14 BeforeSwaps

8. Byt en ekstra gang for individuelt selv magiske firkanter større end 6x6. Ud over skiftet til kvadrant A og D nævnt ovenfor, skal du også lave et skift for kvadrant C og B. Marker kolonnerne fra højre side af firkanten til venstre, én mindre end antallet af kolonner, der er markeret for fremhævning A-1. Skift værdierne i kvadrant C med værdierne i kvadrant B for disse kolonner ved at bruge den samme en-til-en metode.

Her er to billeder af en 14x14 Magic Square før og efter begge switches. Omskiftningsfladen på kvadrant A er markeret med blåt, overfladen for kvadrant D er grøn, for kvadrant C gul og for kvadrant B orange.

Magic Square på 14x14 før skiftet (trin 6, 7 og 8)

Magic Square på 14x14 efter at have udført udskiftningerne (trin 6, 7 og 8)

Metode 3 af 3: Løsning af en dobbelt lige magisk firkant

Billede med titlen Løs en magisk firkant Trin 11

1. Forstå, hvad et dobbelt lige kvadrat er. Et simpelt lige kvadrat har et antal kvadrater pr. side, der er deleligt med 2. Et dobbelt lige kvadrat har et antal kvadrater på hver side, der er delelige med 4.

Den mindste dobbelt lige firkant, der kan laves, er 4x4 firkanten.

Billede med titlen Løs en magisk firkant Trin 12

2. Beregn den magiske konstant. Brug samme metode som for de ulige eller ental lige magiske kvadrater: den magiske konstant = [n * (n2 + 1)] / 2, hvor n = antallet af kvadrater pr. side. Så i eksemplet med en 4x4 firkant:

sum = [4 * (42 + 1)] / 2

sum = [4 * (16 + 1)] / 2

sum = (4 * 17) / 2

sum = 68/2

Den magiske konstant for et 4x4 kvadrat er 68/2 eller 34.

Alle rækker, kolonner og diagonaler skal danne dette tal.

Billede med titlen Løs en magisk firkant Trin 13

3. Påfør markører A-D. I hvert hjørne af den magiske firkant skal du placere en lille firkant med siderne n/4, hvor n = længden af den ene side af hele den magiske firkant. Mærk dem mod uret som markører A, B, C og D.

I en 4x4 firkant skal du blot markere de fire hjørnefirkanter.

I en 8x8 firkant er hver markør et 2x2 område i hjørnerne.

I en 12x12 firkant er hver markør et 3x3 område i hjørnerne osv.

Billede med titlen Løs en magisk firkant Trin 14

4. Sæt det centrale mærke. Marker alle felterne i midten af den magiske firkant i et kvadratisk område med længden n/2, hvor n = længden af hver side af en komplet magisk firkant. Centralmarkøren må ikke overlappe med markørerne A-D, men skal røre ved dem i hjørnerne.

I en 4x4 firkant er den centrale markør et 2x2 område i midten.

I en 8x8 firkant er den centrale markør et 4x4 område i midten osv.

Billede med titlen Løs en magisk firkant Trin 15

5. Udfyld den magiske firkant, men kun i de markerede områder. Begynd at udfylde dine magiske kvadrattal fra venstre mod højre, men placer kun et tal, hvis boksen falder inden for en markør. Så i en 4x4 boks skal du udfylde følgende felter:

1 i den øverste venstre boks og 4 i den øverste højre boks

6 og 7 i de midterste felter i række 2

10 og 11 i de midterste felter i række 3

13 i nederste venstre boks og 16 i nederste højre boks.

Billede med titlen Løs en magisk firkant Trin 16

6. Udfyld resten af den magiske firkant ved at tælle baglæns. Dette er i det væsentlige det omvendte af det foregående trin. Start igen med det øverste venstre felt, men spring denne gang over alle felter, der falder i det markerede område, og udfyld de umarkerede felter ved at tælle tilbage. Start med det største tal i dit nummerområde. Så udfyld i en 4x4 magisk firkant:

15 og 14 i de midterste felter i række 1

12 i det yderste venstre felt og 9 i det yderste højre felt i række 2

8 i det yderste venstre felt og 5 i det yderste højre felt i række 3

3 og 2 i de midterste felter i række 4

På dette tidspunkt skal alle kolonner, rækker og diagonaler have en sum svarende til den tidligere beregnede magiske konstant.